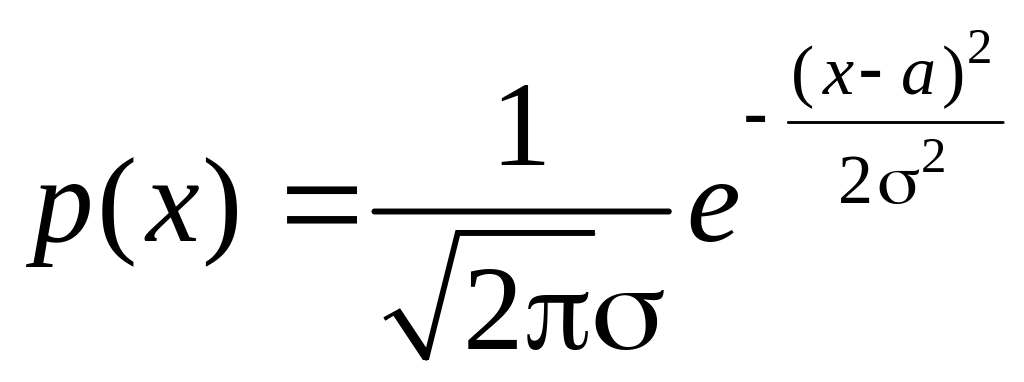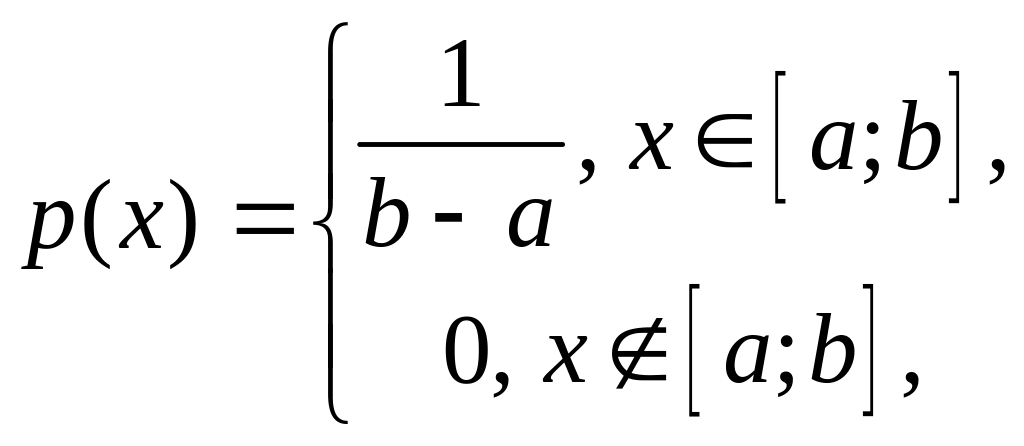- •Основные понятия, используемые в математической обработке психологических данных Признаки и переменные
- •Шкалы измерения
- •Математическая статистика. Первоначальные понятия математической статистики
- •Измерение значений психологических признаков
- •Разные виды случайных выборок
- •Статистическое распределение выборки.
- •Типы выборки
- •Эмпирическая функция распределения.
- •Гистограмма
- •Статистические оценки параметров распределения.
- •Групповая и общая средние
- •Групповая, внутри групповая, межгрупповая и общая дисперсии
- •Интервальные оценки.
- •Доверительные интервалы для оценки среднеквадратического отклонения нормального распределения
- •Характеристики вариационного ряда
- •Обычные, начальные и центральные эмпирические моменты
- •Эмпирические и выравнивающие (теоретические) частоты
- •Асимметрия и эксцесс
- •Метод моментов.
- •Метод наибольшего правдоподобия.
- •Элементы теории линейной корреляции.
- •Статистическая проверка гипотез о виде и о параметрах распределений.
- •Статистический критерий проверки нулевой гипотезы
- •Критерий Пирсона проверки гипотезы о нормальном распределении генеральной совокупности
- •Сравнение двух дисперсий нормальных генеральных совокупностей
- •Сравнение исправленной выборочной дисперсии с гипотетической генеральной дисперсией нормальной совокупности
- •Сравнение двух средних нормальных генеральных совокупностей, дисперсии которых известны (независимые выборки)
- •Сравнение двух средних произвольно распределенных генеральных совокупностей (большие независимые выборки)
- •Сравнение двух средних нормальных генеральных совокупностей, дисперсии которых неизвестны и одинаковы (малые независимые выборки)
- •Сравнение выборочной средней с гипотетической генеральной средней нормальной совокупности
- •Связь между двусторонней критической областью и доверительным интервалом
- •Определение минимального объема выборки при сравнении выборочной и гипотетической генеральной средних
- •Сравнение двух средних нормальных генеральных совокупностей с неизвестными дисперсиями (зависимые выборки)
- •Сравнение наблюдаемой относительной частоты с гипотетической вероятностью появления события
- •Сравнение двух вероятностей биномиальных распределений
- •Сравнение нескольких дисперсий нормальных генеральных совокупностей по выборкам различного объема. Критерий Бартлетта
- •Сравнение нескольких дисперсий нормальных генеральных совокупностей по выборкам одинакового объема. Критерий Кочрена
- •Проверка гипотезы о значимости выборочного коэффициента корреляции
- •Выборочный коэффициент ранговой корреляции Спирмена и проверка гипотезы о его значимости
- •Выборочный коэффициент ранговой корреляции Кендалла и проверка гипотезы о его значимости
- •Критерий Вилкоксона и проверка гипотезы об однородности двух выборок
- •Однофакторный дисперсионный анализ Сравнение нескольких средних. Понятие о дисперсионном анализе
- •Общая факторная и остаточная суммы квадратов отклонений
- •Общая, факторная и остаточная дисперсии
- •Сравнение нескольких средних методом дисперсионного анализа
- •Критические точки распределения
- •Критические точки распределения Стьюдента
- •Критические точки распределения f Фишера — Снедекора
- •Критические точки распределения Кочрена
- •Критические точки распределения Кочрена (продолжение)
- •Критические точки критерия Вилкоксона
- •Критические точки критерия Вилкоксона (продолжение)
- •Критические точки критерия Вилкоксона (продолжение)
Эмпирическая функция распределения.
Определим для каждого действительного
числа x случайную величину
![]() ,
равную числу элементов выборки x1,
x2, ..., xk,
значения которых не превосходят x,
т.е.
равно числу элементов множества { j|
xj < x } и положим
,
равную числу элементов выборки x1,
x2, ..., xk,
значения которых не превосходят x,
т.е.
равно числу элементов множества { j|
xj < x } и положим
![]() .
.
Функция
![]() называется эмпирической функцией
распределения, соответствующей данной
выборке. Функцию распределения
называется эмпирической функцией
распределения, соответствующей данной
выборке. Функцию распределения
![]() наблюдаемой случайной величины
в этом случае называют теоретической
функцией распределения. По своему
определению эмпирическая функция
распределения – случайная функция.
Значениями функции
являются
числа
наблюдаемой случайной величины
в этом случае называют теоретической
функцией распределения. По своему
определению эмпирическая функция
распределения – случайная функция.
Значениями функции
являются
числа
![]() и при этом
и при этом
![]() .
.
Для каждой реализации x выборки X функция однозначно определена и обладает всеми свойствами функции распределения:
1) изменяется от 0 до 1,
2) не убывает и непрерывна справа.
Отметим также, что кусочно-постоянна.
Эмпирическая функция распределения – некоторая характеристика выборки. Эта функция играет фундаментальную роль в математической статистике. Важнейшее ее свойство состоит в том, что при увеличении числа испытаний над случайной величиной происходит сближение этой функции с теоретической функцией распределения изучаемого признака. Смысл этого утверждения раскрывает следующая теорема.
Теорема. Пусть
-
эмпирическая функция распределения,
построенная по выборке X и
–
соответствующая теоретическая функция
распределения. Тогда для любого
![]() и для любого
и для любого
![]()
![]() .
.
Таким образом, если объем выборки большой, то значение эмпирической функции распределения в каждой точке x может служить приближенным значением теоретической функции распределения в этой точке. Функцию - часто называют статистическим аналогом для .
Гистограмма
Как мы видели, эмпирическая функция распределения является одним из способов представления статистических данных. Другим способом наглядного представления статистических данных являются гистограммы.
Для построения гистограммы область
значений случайной величины
разбивают на равные интервалы. Для
заданной реализации x=(x1,...,xn).
выборки x подсчитывают число координат
xi, попавших в соответствующие
интервалы, и на каждом интервале, как
на основании, строят прямоугольник с
высотой
![]() ,
где h- длина интервала,
,
где h- длина интервала,
![]() - число элементов выборки, попавших в
данный интервал. Полученную при этом
фигуру называют гистограммой.
- число элементов выборки, попавших в
данный интервал. Полученную при этом
фигуру называют гистограммой.
Поскольку площадь каждого полученного
прямоугольника равна
![]() ,
т.е. относительной частоте попадания
выборочных значений в соответствующий
интервал, по теореме Бернулли эта частота
сходится при
,
т.е. относительной частоте попадания
выборочных значений в соответствующий
интервал, по теореме Бернулли эта частота
сходится при
![]() к вероятности попадания случайной
величины
в соответствующий интервал. Таким
образом, при большом значении объема
выборки n и достаточно малом h
высоты построенных прямоугольников
можно рассматривать в качестве
приближенных значений для плотности
p(x).
к вероятности попадания случайной
величины
в соответствующий интервал. Таким
образом, при большом значении объема
выборки n и достаточно малом h
высоты построенных прямоугольников
можно рассматривать в качестве
приближенных значений для плотности
p(x).
Отсюда следует, что верхнюю границу гистограммы можно рассматривать как статистический аналог плотности распределения наблюдаемой случайной величины. Однако, гистограмму рекомендуется применять на предварительном этапе анализа статистических данных.
В методе гистограмм неизвестная плотность распределения приближается кусочно-постоянным графиком. Если плотность p(x)- достаточно гладкая, то, как известно, такие функции лучше приближать кусочно-линейными функциями. Итак, полигон частот это ломаная, которая строится так: если построена гистограмма, то ординаты, соответствующие средним точкам интервалов, последовательно соединяют отрезками прямых. Построенный таким образом кусочно-линейный график также является статистическим аналогом теоретической плотности.
Приведем пример графической обработке данных эксперимента. Так, пусть в результате измерения некоторой величины получены следующие данные:
|
2 |
3 |
5 |
6 |
10 |
15 |
20 |
25 |
30 |
|
5 |
6 |
10 |
15 |
20 |
24 |
20 |
10 |
5 |
Для построения гистограммы область
значений случайной величины X
разобьем на равные интервалы. Поскольку
область значений величины Х находится
в промежутке [2, 30], то нам удобнее будет
изображать гистограмму взяв в качестве
исходного промежутка множество [0, 30].
Это множество разобьем на 6 частей
точками 5, 10,15,20,25. Затем подсчитаем
![]() -(j=1,2,3,4,5,6)
– количество координат
попавших соответственно в промежутки
-(j=1,2,3,4,5,6)
– количество координат
попавших соответственно в промежутки
I1=[0, 5), I2=[5, 10), I3=[10, 15), I4=[15, 20), I5=[20, 25), I6=[25, 30].
Так в нашем
случае
![]() =11,
=11,
![]() =25,
=25,
![]() =20,
=20,
![]() =24,
=24,
![]() =20,
=20,
![]() =15.
Поскольку объем нашей выборки равен
=
=15.
Поскольку объем нашей выборки равен
=![]() =120
, то нам остается на каждом из интервалов
Ij построить прямоугольники с
высотой
=120
, то нам остается на каждом из интервалов
Ij построить прямоугольники с
высотой
![]() ,
где
,
где
![]() -
длина интервалов Ij.
-
длина интервалов Ij.
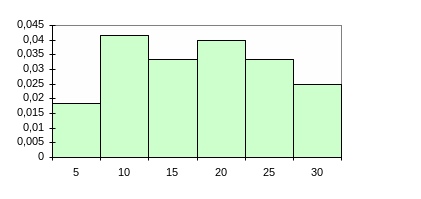
Выбрав подходящий масштаб по оси Оу мы получим следующую гистограмму:
В заключение рассмотрим плотности некоторых, часто встречающиеся, распределений:
Нормальное (два неизвестных
параметра):
|
Равномерное (два неизвестных
параметра):
|
Биномиальное (один
неизвестный параметр):
|
Пуассоновское (один
неизвестный параметр):
|