6 Определение случайного процесса и случайной функции. Характеристики случайных функций: мат. Ожидание, дисперсия и корреляционная функция

6.1 Определение случайного процесса и случайной функции

Случайной называется функция, которая в результате опыта принимает конкретный вид, заранее неизвестно, какой.

Случайная функция, аргументом которой является время, называется случайным процессом.

Пусть в результате опыта зафиксировано n реализаций случайной функции x_i, i=1,2,..,n.

Зафиксируем аргумент t на некотором значении t=t₀. При этом случайная функция Х(t) превращается в случайную величину, которая называется сечением случайной функции.

Случайная функция есть бесконечной системой случайных величин.

6.2 Характеристики случайных функций

Характеристиками случайных функций в общем виде являются функции!!!

1) Математическим ожиданием m_x(t) случайной функции X(t) является неслучайная функция аргумента t, равная для каждого значения аргумента математическому ожиданию соответствующего сечения.

2) Дисперсией случайной функции X(t) называется неслучайная функция, равная для каждого аргумента t дисперсии соответствующего сечения.

3) СКО случайной функции X(t) является корень из дисперсии.

4) Корреляционной функцией K_x(t, t′) называется неслучайная функция двух аргументов, равная для каждой пары аргументов корреляционному моменту соответствующих сечений.

Свойства корреляционной функции

1) Как правило, убывает при увеличении модуля разности | t-t′|.

2) Симметрична относительно аргумента.

3) Если t=t′, то корреляционная функция равна дисперсии случайной функции.

Размерность корреляционной функции равна х²(t). Корреляционная функция зависит от масштаба Х. Для устранения этого недостатка вводится понятие нормированной корреляционной функции.

Корреляционная матрица представляет собой приближенную аппроксимацию корреляционной функции, более точную при большем разбиении случайной функции на случайные величины.

При прибавлении к случайной функции неслучайного слагаемого ее мат. ожидание увеличивается на величину этого слагаемого, а корреляционная функция не изменяется.

При умножении случайной функции на неслучайную функцию φ(t) (или постоянную) ее мат. ожидание умножается на эту же функцию, а корреляционная функция умножается на множитель φ(t)* φ(t′).

Практика

1 Формулы полной вероятности и Байеса

1.1 Полная вероятность

Пусть событие А может произойти лишь после наступления одного из несовместных событий В_і, і=1,2,…,n, образующих полную группу. Тогда вероятность события А равна сумме произведений вероятностей событий В_i на соответствующую условную вероятность события А.

Расчетная формула полной вероятности:

Пример 1. В первой урне 4 черных и 2 белых шара, во второй — 6 черных и 5 белых, в третьей — 2 черных и два белых.

Найти вероятность того, что при извлечении шара из наудачу выбранной урны, шар окажется белым.

Решение. Событие А — извлечение белого шара из наудачу выбранной урны.

Событие В_i — выбор i-й урны.

Тогда вероятность каждого из событий В_i равняется .

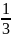Найдем вероятность события А:

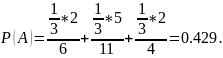
Пример 2. В первой коробке 20 деталей, из них 18 стандартных, во второй коробке 10 деталей, из них 9 стандартных. Из второй коробки наудачу взята одна деталь и переложена в первую.

Найти вероятность того, что наудачу извлеченная после этого из первой коробки деталь окажется стандартной.

Решение. Событие А — извлечение стандартной детали из первой коробки.

Событие В₁ — в первую коробку поместили стандартную деталь.

Событие В₂ — в первую коробку поместили нестандартную деталь.

Вероятность события В₁: .

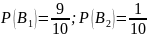Тогда вероятность события А: .
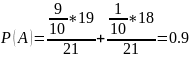