
- •60. Классификация линейных дифференциальных уравнений второго порядка с частными производными и приведение их к каноническому виду.
- •61. Вывод уравнения теплопроводности.
- •62. Задача Коши для уравнения колебаний струны. Формула Даламбера.
- •63. Решение первой краевой задачи для однородного уравнения колебаний струны методом разделения переменных.
- •64. Принцип максимума и теорема единственности решения первой краевой задачи для уравнения теплопроводности.
- •65. Теоремы единственности решения задачи Дирихле и задачи Неймана для уравнения Лапласа.
63. Решение первой краевой задачи для однородного уравнения колебаний струны методом разделения переменных.
Рассматривается
краевая задача utt=a2uxx,
0 < x
< l, t
> 0, (1)
u(0,t)=0,
u(l,t)=0, t > 0, (2)
u(x,0)=u0(x),
ut(x,0)=u1(x),
0
< x
< l.
(3) Решение
уравнения (1)
будем искать в виде u(x,t)=X(x)T(t). Подставляя
это выражение в уравнение (1),
получим a2X’’(x)T(t)=T’’(t)X(x).
Поделим обе части последнего равенства
на a2X(x)T(t).
Получим
![]() В уравнении (4)
левая часть есть функция переменной x,
а правая - функция переменной t,
следовательно, равенство (4)
может быть выполнено при всех x, t из
рассматриваемой области, лишь при
условии, что и левая и правая его части
на самом деле есть постоянные:
В уравнении (4)
левая часть есть функция переменной x,
а правая - функция переменной t,
следовательно, равенство (4)
может быть выполнено при всех x, t из
рассматриваемой области, лишь при
условии, что и левая и правая его части
на самом деле есть постоянные:
![]()
=
const. Знак минус здесь использован лишь
для удобства дальнейших записей. Таким
образом, для отыскания функций X(x), T(t)
получаем обыкновенные дифференциальные
уравнения
![]() Потребовав, чтобы функция удовлетворяла
не только уравнению (1),
но и граничным условиям (2),
получим граничные условия для функции
X:
Потребовав, чтобы функция удовлетворяла
не только уравнению (1),
но и граничным условиям (2),
получим граничные условия для функции
X:
![]() Задача (6),
(8)
называется задачей Штурма-Лиувилля.
Функция X, не равная тождественно нулю,
удовлетворяющая уравнению (6)
и граничному условию (8)
при некотором ,
называется собственной функцией задачи
Штурма-Лиувилля; соответствующее
значение параметра
называется собственным числом задачи
Штурма-Лиувилля. Собственные функции
и собственные числа рассматриваемой
нами задачи Штурма-Лиувилля мы найдем
в явном виде. Покажем сначала что
собственные числа этой задачи могут
принимать только положительные значения.
Действительно, если
< 0, то общее решение обыкновенного
дифференциального уравнения (6)
имеет вид X(x)=c1e-x+c2
e--x.
Граничные условия (8)
порождают систему линейных алгебраических
уравнений для параметров c1, c2:
c1+c2=0,
c1e-
L
+C2
e--
L=0
определитель которой равен e--
L
- e-
L
и очевидно отличен от нуля. Поэтому
рассматриваемая система имеет только
тривиальное решение: c1=c2=0,
следовательно задача (6),
(8)
при
> 0 может иметь только тривиальное
решение. Пусть теперь
= 0. Общее решение уравнения в этом случае
есть X(x)=c1x+c2.
Граничные условия (8)
вновь могут быть выполнены лишь при
c1=c2=0,
то есть и
= 0 не может быть собственным значением
задачи Штурма-Лиувилля. Остается принять,
что
< 0. В этом случае общее решение уравнения
(6),
записанное в тригонометрической форме,
имеет вид X(x)=c1cos x+c2sin x.
Удовлетворяя граничные условия (8),
получим c1=0, c2sinL=0.
Естественно, мы должны принять, что
c20,
но тогда sinL=0,
откуда получаем, что =n=((n)/L)2,
n=1,2,…. Этим значениям параметра
соответствуют нетривиальные решения
X(x)=c2Xn(x)=sin((n)/L)x
задачи (6),
(8).
Итак, n, c2Xn(x)
n=1,2,… - собственные числа и
соответствующие им собственные функции
задачи Штурма-Лиувилля. Естественно,
что собственные функции как решения
однородного уравнения определяются с
точностью до постоянного множителя. В
дальнейшем постоянную c2
удобно считать равной единице. Пусть
теперь Tn - общее
решение уравнения (7)
при
Задача (6),
(8)
называется задачей Штурма-Лиувилля.
Функция X, не равная тождественно нулю,
удовлетворяющая уравнению (6)
и граничному условию (8)
при некотором ,
называется собственной функцией задачи
Штурма-Лиувилля; соответствующее
значение параметра
называется собственным числом задачи
Штурма-Лиувилля. Собственные функции
и собственные числа рассматриваемой
нами задачи Штурма-Лиувилля мы найдем
в явном виде. Покажем сначала что
собственные числа этой задачи могут
принимать только положительные значения.
Действительно, если
< 0, то общее решение обыкновенного
дифференциального уравнения (6)
имеет вид X(x)=c1e-x+c2
e--x.
Граничные условия (8)
порождают систему линейных алгебраических
уравнений для параметров c1, c2:
c1+c2=0,
c1e-
L
+C2
e--
L=0
определитель которой равен e--
L
- e-
L
и очевидно отличен от нуля. Поэтому
рассматриваемая система имеет только
тривиальное решение: c1=c2=0,
следовательно задача (6),
(8)
при
> 0 может иметь только тривиальное
решение. Пусть теперь
= 0. Общее решение уравнения в этом случае
есть X(x)=c1x+c2.
Граничные условия (8)
вновь могут быть выполнены лишь при
c1=c2=0,
то есть и
= 0 не может быть собственным значением
задачи Штурма-Лиувилля. Остается принять,
что
< 0. В этом случае общее решение уравнения
(6),
записанное в тригонометрической форме,
имеет вид X(x)=c1cos x+c2sin x.
Удовлетворяя граничные условия (8),
получим c1=0, c2sinL=0.
Естественно, мы должны принять, что
c20,
но тогда sinL=0,
откуда получаем, что =n=((n)/L)2,
n=1,2,…. Этим значениям параметра
соответствуют нетривиальные решения
X(x)=c2Xn(x)=sin((n)/L)x
задачи (6),
(8).
Итак, n, c2Xn(x)
n=1,2,… - собственные числа и
соответствующие им собственные функции
задачи Штурма-Лиувилля. Естественно,
что собственные функции как решения
однородного уравнения определяются с
точностью до постоянного множителя. В
дальнейшем постоянную c2
удобно считать равной единице. Пусть
теперь Tn - общее
решение уравнения (7)
при
![]() =n: Tn(t)=ancos(a2n) t+bnsin(a2n) t,
или (после элементарных преобразований)
=n: Tn(t)=ancos(a2n) t+bnsin(a2n) t,
или (после элементарных преобразований)
![]() .
В силу определения функций Xn,
Tn
получаем, что функция
.
В силу определения функций Xn,
Tn
получаем, что функция
![]() при любых n=1,2,… и любых значениях
постоянных an, bn
удовлетворяет уравнению (1)
и граничным условиям (2).
Решение уравнения (1),
удовлетворяющее также и начальным
условиям будем разыскивать в виде
бесконечной суммы
при любых n=1,2,… и любых значениях
постоянных an, bn
удовлетворяет уравнению (1)
и граничным условиям (2).
Решение уравнения (1),
удовлетворяющее также и начальным
условиям будем разыскивать в виде
бесконечной суммы
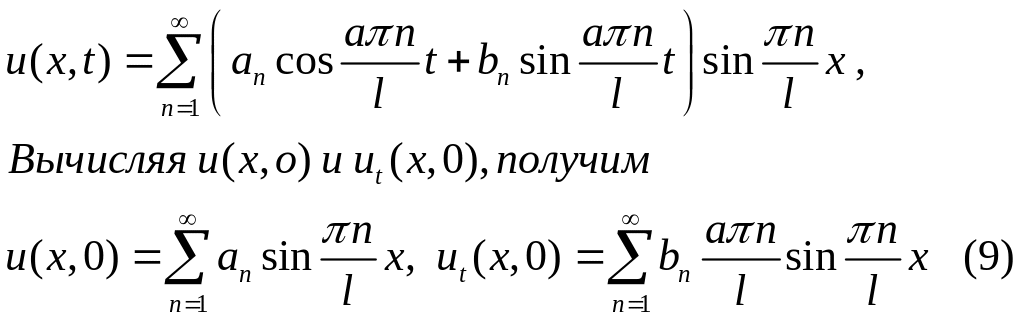 Предположим
теперь, что функции u0, u1
могут быть представлены в виде разложений
в ряд Фурье по синусам
Предположим
теперь, что функции u0, u1
могут быть представлены в виде разложений
в ряд Фурье по синусам
![]() Коэффициенты
Фурье вычисляются по известным из курса
математического анализа формулам
Коэффициенты
Фурье вычисляются по известным из курса
математического анализа формулам
![]() Сравнивая равенства (9)
и (10),
получаем, что начальные условия (3)
выполняются, если положить
Сравнивая равенства (9)
и (10),
получаем, что начальные условия (3)
выполняются, если положить
![]() Таким образом решение задачи (1)-(3)
построено. Следует однако отметить, что
это - формальное решение. При некоторых
условиях на функции u0, u1
можно показать, что ряд, определяющий
функцию u, а также ряды, получаемые по
членным дифференцированием этого ряда
дважды по x и по t, равномерно сходятся
при 0
x
l, t
0, и, следовательно, полученная нами
формула действительно определяет
решение задачи (1)-(3).
Таким образом решение задачи (1)-(3)
построено. Следует однако отметить, что
это - формальное решение. При некоторых
условиях на функции u0, u1
можно показать, что ряд, определяющий
функцию u, а также ряды, получаемые по
членным дифференцированием этого ряда
дважды по x и по t, равномерно сходятся
при 0
x
l, t
0, и, следовательно, полученная нами
формула действительно определяет
решение задачи (1)-(3).
