1, Модель парной регрессии

Линейная регрессия находит широкое применение в эконометрике в виде чёткой экономической интерпретации её параметров.

Линейная регрессия сводится к нахождению уравнения вида (1) или (2). Уравнение (1) позволяет по заданным значениям фактора х иметь теоретические значения результативного признака, подставляя в него фактические значения фактора х. Уравнение (2) рассматривает у как зависимую переменную, состоящую из двух составляющих:

1) неслучайную составляющую , где выступает как объясняющая (независимая) переменная, а и - параметры уравнения;

2) случайного члена - (возмущение)

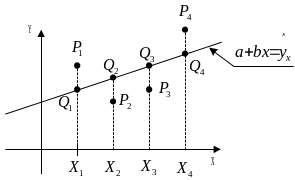
x	x1	x2	x3	x4
y	y1	y2	y3	y4

Если , то получатся точки .

Если , то получим точки .

Случайный член существует по ряду причин:

1) невключение объясняющих переменных (есть ещё другие факторы, влияющие на у), но измерить их невозможно (например, психологические);

2) агрегирование переменных (объединение некоторого числа микроэкономического соотношения);

3) неправильное описание структуры модели (временные ряды зависят не только от t, но и от t-1);

4) неправильная функциональная спецификация (не линейная, а какая-то другая);

5) ошибки измерения.

ε_i = сумма всех этих факторов.

Рассмотрим задачу определения параметров модели, то есть коэффициентов и - оценке параметров модели.

Оценки параметров линейной регрессии могут быть найдены разными методами, например можно построить поле корреляции, взять 2 точки и провести через них прямую.

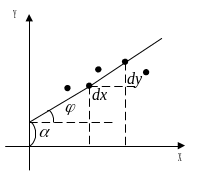
оценка параметра , то есть отрезок отсекаемой прямой на оси ;

, - угловой коэффициент прямой,

- оценка параметра .

Необходимо с самого начала признать, что мы не сможем рассчитать истинные значения и . Мы можем получить только оценки, и они могут быть или хорошими или плохими. Построение линии регрессии на глаз является достаточно субъективным.

Отрезок ε₁ (остаток), ε₂. Остатки должны быть min. .

Существует целый ряд критериев:

1. МНК min суммы квадратов отклонений.

2. Минимизируется сумма модулей отклонений.

3. Функция Хубера , где - «мера» с которой отклонение входит в функционал.

Рассмотрим достоинства и недостатки перечисленных функционалов.

1) сумма квадратов отклонений:

«+» лёгкость вычисления, хорошие статистические свойства, простота математических выводов делают возможным построить развитую теорию, позволяющую провести тщательную проверку различных статистических гипотез;

«-» чувствительность к выбросам;

2) сумма модулей отклонений:

«+» робастость, то есть нечувствительность к выбросам;

«-» сложность вычислительной процедуры, большим отклонениям надо придавать больший вес (лучше 2 отклонения по 1, чем одно 0 и 2), неоднозначность, то есть разным значениям параметра могут соответствовать одинаковые суммы модулей отклонений.

Функция Хубера является попыткой совместить достоинства двух первых функционалов.

Рассмотрим МНК:

Из множества линий регрессии на графике выбирается та, сумма квадратов отклонений была минимальной.

Чтобы найти min надо взять частные производные по и функции S и приравнять их нулю.

Получим систему нормальных уравнений для оценки параметров a и b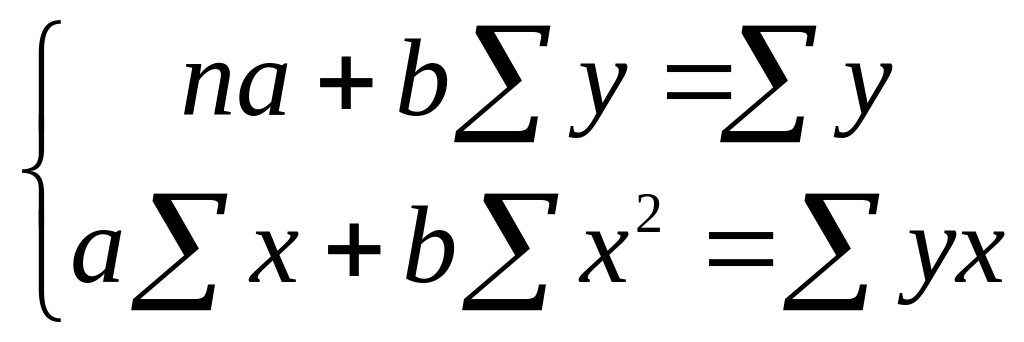. (3)

(3)

Решая систему (3) любым методом: исключение, Крамера (через определители), найдем оценки параметров a и b. МНК даёт самые точные несмещённые и эффективные оценки и .

Можно воспользоваться формулами: если 1 уравнение системы (3)

- ковариация признаков;

- дисперсия признака х.

Параметр b называется коэффициентом регрессии. Его величина показывает среднее изменение результата (у) с изменением фактора х на одну единицу. Зависимость между расходами на питание (у) и располагаемым личным доходом (х) за период 1959 по 1983 г. В США описывается уравнением регрессии.

, х увеличился на 1 единицу, а у на 0,093ед.

Х увеличился на 1 млрд $, то у (расходы на питание) возрастут на 93 млн $ (т. е. из 1 $ дохода 9,3 цента – на питание).

Параметр а, . Уравнение регрессии теряет смысл, «а» - не имеет экономического содержания. Интерпретировать можно только знак при параметре а. - относительное изменение параметра у, происходит медленнее, чем изменение фактора или вариации результата.

Коэффициенты вариации ; ;

Если , то ;

Если , то

Возможность чёткой экономической интерпретации коэффициента регрессии сделала линейное уравнение регрессии достаточно распространенным в экономических исследованиях.

Статистические свойства оценок метода наименьших квадратов.

Поскольку полученные оценки a и b коэффициентов линейной рег­рессии опираются на статистические данные и являются случайными величинами, то естественно установить свойства названных оценок; как случайных величин. Более того, не выяснив этих свойств, невоз­можно сделать обоснованные выводы относительно качества и надеж­ности полученных оценок. Необходимо, в частности, определить такие их статистические характеристики, как математическое ожидание и дисперсия. К желательным свойствам оценок относятся также несмещенность и состоятельность. Далее, если бы удалось установить вид распределения (плотности распределения) оценок, можно было бы по­строить доверительные интервалы для истинных значений параметров регрессии (т. е. получить интервальные оценки коэффициентов) и реа­лизовать процедуры проверки гипотез относительно их значений. Важ­ную роль играет также изучение статистических свойств остатков оце­ненной регрессии.

Все эти задачи можно решить, основываясь на некоторых правдопо­добных теоретических предпосылках (гипотезах) модели, выполнение которых на практике подлежит проверке с помощью специально разра­ботанных для этого статистических процедур.

Основные предпосылки РА ( ε_i – случайная величина, x_i – неслучайная величина):

Предположение относительно независимых переменных

В дальнейшем будем допускать, что х — детерминированная (не­случайная) величина, т. е. значения независимых переменных заранее известны. Данное предположение (предпосылка), к сожалению, на практике при моделировании реальных социально-экономических процессов часто не выполняется. Это связано с тем, что здесь в качест­ве независимых переменных часто выступают стохастические некон­тролируемые величины, такие как интенсивность потока покупателей (в одном из примеров главы 1) или рыночный индекс в рыночной мо­дели, который также является случайной величиной. При нарушении вышеупомянутой предпосылки ряд «хороших» свойств оценок сохра­няется (при некоторых условиях), но в отдельных случаях требуется корректировка модели (оценок).

Предположения относительно случайной составляющей модели

При выполнении предпосылки относительно переменной х стати­стические свойства оценок параметров и зависимой переменной, а так­же, остатков, целиком определяются вероятностными свойствами случайной составляющей регрессионной модели. Относительно слу­чайной составляющей в классическом регрессионном анализе предпо­лагают выполнение следующих условий, которые называются условия­ми Гаусса-Маркова и играют ключевую роль при изучении свойств оце­нок, полученных по методу наименьших квадратов:

1. Первое условие заключается в том, что математическое ожидание случайной составляющей во всех наблюдениях должно быть равно нулю. Формально это записывается так

М{ε_t} = 0, для всех t = 1,2,...,п.

Смысл этого условия заключается в том, что не должно быть систе­матического смещения случайной составляющей. В линейной регрес­сии систематическое смещение линии регрессии учитывается с помо­щью введения параметра смещения ε_i и поэтому данное условие можно считать всегда выполненным.

2. Дисперсия случайной составляющей постоянна для всех наблю­дений (т. е. не зависит от номера наблюдения). Это условие записыва­ется так:

D{ε_t}=M{ε_t²}=σ²,

где дисперсия σ² — величина постоянная.

Это свойство дисперсии ошибок называется гомоскедастичностью (однородностью) (запомните этот термин).

Выполнение условия гомоскедастичности при построении конкрет­ных эконометрических моделей необходимо проверять с помощью спе­циальных статистических процедур. Поскольку истинные дисперсии ошибок неизвестны, их можно лишь приближенно оценить на основе наблюдаемых (точнее, вычисляемых) значений остатков модели в каж­дом наблюдении. Таким образом, и свойство гомоскедастичности на практике проверяется (диагностируется) на самом деле для остатков мо­дели, а не для истинных ошибок, и может выполняться лишь прибли­женно. Если условие гомоскедастичности не выполнено (т. е. дисперсия ошибок не постоянна), то говорят, что имеет место условие гетероскедастичности (запомните этот термин). Понятия «гомоскедастичность» и «гетероскедастичность» являются ключевыми в эконометрике.

Графическая иллюстрация понятий «гомоскедастичность» и «гетероскедастичность»

Рис. 2.6а

Гомоскедастичность Рис.2.6б Рис. 2.6в

Гетероскедастичность Гетероскедастичные остатки

3. Случайные составляющие модели для различных наблюдений некоррелированы. Это условие записывается таким образом:

М{εi, εj}=0, для всех i≠j (i, j=1,2,…,n)

Выполнение данного условия означает отсутствие систематической (статистической) связи между значениями случайного члена в любых двух наблюдениях. Это свойство на практике также проверяется с по­мощью статистических процедур на основе анализа остатков модели.

Если оно нарушается, то процедура оценки параметров должна быть скорректирована.

4. Четвертое условие Гаусса-Маркова записывается так:

M{x_I, εj}=0, для всех i и j,

и означает, что объясняющие переменные и случайные составляющие некоррелированы для всех наблюдений. Ранее мы предположили, что объясняющая переменная в модели не является стохастической. В этом случае четвертое условие выполняется автоматически.

Регрессионная модель с детерминированными регрессорами, удовлетво­ряющая предпосылкам Гаусса-Маркова, называется классической регрес­сионной моделью.

Дополнительное предположение о нормальном распределении ошибок

При выполнении условий Гаусса-Маркова, оценки наименьших квадратов обладают такими свойствами, как несмещенность, состоя­тельность и оптимальность (эффективность). Однако, для построения доверительных интервалов и проверки гипотез относительно истинных значений параметров, необходимо дополнительное предположение о распределении случайной составляющей ε_i. В классическом регресси­онном анализе допускается, что эта составляющая распределена по нормальному закону и тогда модель называют классической нормальной линейной регрессией. (1-4) достаточно, а 5 необходимо для оценки точности уравнения регрессии.

Данное предположение является, пожалуй, наиболее спорным. Дело в том, что предположение о нормальности можно считать правдо­подобным, если значения случайной величины порождаются в резуль­тате воздействия большого количества независимых случайных факто­ров, каждый из которых не обязательно имеет нормальное распределе­ние. Примером такого воздействия является так называемое броуновское движение (хаотичное движение малых частиц в жидкости как результат совокупного воздействия на частицу — ударов, соударе­ния — большого количества молекул жидкости).

В экономических процессах распределения случайных величин, как правило, отличаются от нормального, поскольку механизм их по­рождения более сложный. Тем не менее, чаще всего именно нормаль­ное распределение используется в эконометрических исследованиях (как, впрочем, и в статистике). Это обусловлено следующими причинами. Во-первых, нормальный закон действительно часто достаточно хорошо (с приемлемой для практики точностью) аппроксимирует (приближенно описывает) распределение случайной составляющей. Во-вторых, что очень важно, на основе нормального распределения можно получить процедуры проверки гипотез и построения доверительных интервалов, удобные для расчетов и применения на практи­ке. В любом случае, не изучив базовые результаты (процедуры), осно­ванные на предположении нормальности, нельзя продвигаться на бо­лее высокий уровень изучения и применения более реалистичных моделей, не использующих эту предпосылку и позволяющих получать более точные результаты.

Замечание. Если случайные величины в модели распределены по нормальному закону, то из свойств некоррелированности в третьем и четвертом условиях Гаусса-Маркова следует и независимость соответ­ствующих случайных величин.

Оценкой модели является уравнение:

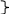
а - оценка они определяются МНК

b - оценка

Несмещенная оценка остаточной дисперсии учитывает воздействие факторов и ошибок неучтенных в модели, определяется с помощью дисперсии возмущения (ошибок) или остаточной дисперсии σ², - это выборочная остаточная дисперсия.

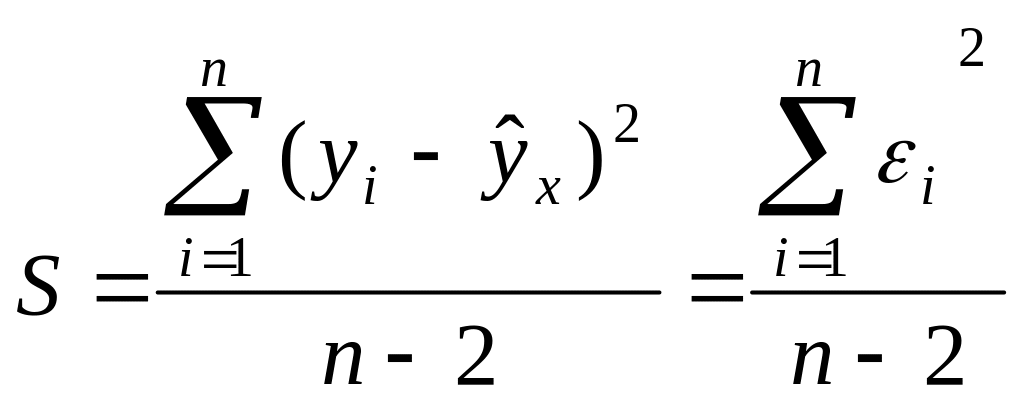
Являются ли оценки a, b и s² наилучшими выясняется по условиям Гаусса-Маркова: если регрессионная модель удовлетворяет предпосылкам 1-4, то оценки a и b имеют наименьшую дисперсию в классе линейных несмещенных оценок.

Свойства выборочных вариаций (дисперсий) и ковариаций.

Для дальнейшего изложения нам понадобится установить ряд пра­вил, которые можно использовать при преобразовании выражений, со­держащих выборочные вариации и ковариации.

Пусть а — некоторая постоянная, а х, у, z — переменные, прини­мающие в i-м наблюдении значения x_i,y_i,z_i,i=1,..., п (n — количество наблюдений). Тогда а можно рассматривать как переменную, значение которой в i-м наблюдении равно а, и

Соv(х, а) =

откуда следует свойство:

1. Cov(x, a) = 0.

Далее, нетрудно видеть, что имеют место равенства:

2. Cov(x, у) = Cov(y, х);

3. Cov(x, x) = Var(x).

Кроме того,

Cov(ax, y) = =

откуда следует свойство:

4. Cov(ax. у) = aCov(x, у).

Далее, имеем

Cov(xy,z) = =

так что можно сформулировать еще одно свойство:

5. Cov(x. у + z) =Cov(x, у) + Cov(x,z).

На основе вышеназванных свойств находим, что

6. Var(a)=0 ,

т. е. постоянная не обладает изменчивостью и

7. Var(ax)=a²Var(x).

Таким образом, при изменении единицы измерения переменной в раз, во столько же раз преобразуется и величина стандартного отклоне­ния этой переменной (напомним, что стандартное отклонение равно квадратному корню из дисперсии).

8. Var(x+a)=Var(x)

т. е. сдвиг начала отсчета не влияет на вариацию переменной.

Далее, имеем:

Var(x+y)=Cov(x+y,x+y)= Cov(x, х) + Cov(x, у) + Cov(y, x) + Cov(x, у).

Таким образом, доказано свойство

9.Var(x+y)=Var(x)+Var(y)+2Cov(x,y),

означающее, что вариация суммы двух переменных отличается от сум­мы вариаций этих переменных на величину, которая равна удвоенному значению ковариации между названными переменными.

Свойства остатков

Теперь установим почти очевидные соотношения, которые следуют из условии минимума критерия наименьших квадратов. Определим величину

ŷ_i=a +bx,

— оценку переменной у при оптимальных значениях коэффициентов регрессии и фиксированном значении х в i-ом наблюдении. Такую оценку называют прогнозом зависимой переменной. Тогда, очевидно, ошибка модели в i-ом наблюдении будет равна ε_i=y_i - ŷ_i и из условия следует, что

т. е сумма квадратов ошибок оценок переменной у (остатков модели) при оптимальных параметрах регрессии а и b равна нулю.

Далее, вытекает, что

т. е., при оптимальных параметрах регрессии ошибки ортогональны на­блюдениям независимой переменной.

Несмещенность МНК-оценок

Статистическая оценка некоторого параметра называется несме­щенной, если ее математическое ожидание равно истинному значению этого параметра.

Для случая парной линейной регрессии это означает, что опенки а и b будут несмещенными, если

М{а} = α,

M{b}=β.

Докажем это свойство. Используя правила преобразования выбо­рочных ковариаций, можно записать:

Cov(x, у) = Cov(x[a + βx + и]) =

= Cov(x, а) + Cov(x, βх) + Cov(x, и) = βVar(x) + Cov(x, и).

Применив формулу для коэффициента, а также полученное выше соотношение, составим выражение:

Далее, поскольку х — неслучайная величина, будем иметь:

и, таким образом, оценка b является несмещенной.

Несмещенность оценки а следует из цепочки равенств:

М{а}=

Замечание. Свойство несмещенности оценок можно доказать и при более слабой форме 4-го условия Гаусса-Маркова, когда х—случайная, но некоррелированная со случайной переменной ε, величина.

Состоятельность оценок

Свойство состоятельности оценок заключается в том, что при неог­раниченном возрастании объема выборки, значение оценки должно стремиться (по вероятности) к истинному значению параметра, а дис­персии оценок должны уменьшаться и в пределе стремиться к нулю. Дисперсии оценок коэффициентов регрессии определяются выраже­ниями:

;

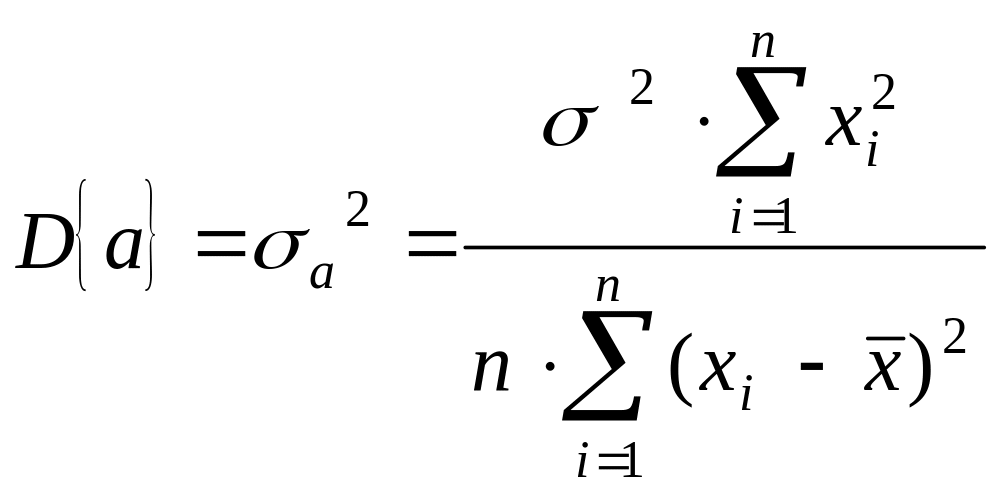Или, используя равенство , можно записать в виде:

Вывод: чем больше число наблюдений n, тем меньше будут дисперсии ошибок.

Эффективность (оптимальность) оценок

До сих пор мы говорили об оптимальности оценок в смысле мини­мума квадратичного критерия. Оказывается, что при выполнении условий Гаусса-Маркова они являются также оптимальными в смысле минимума дисперсии.

Оценка называется эффективной, если она имеет минимальную дис­персию по сравнению с другими оценками заданного класса.

Таким образом, оценки наименьших квадратов являются эффек­тивными, т. е. наилучшими в смысле минимума диспепсии, в классе всех линейных несмещенных оценок параметров.

Рассмотрим функции плотности вероятности и одиночного наблюдения и выборочного среднего.

Величина х считается распределённой. Распределения и симметрично относительно -теоретического среднего. Разница в том, что распределение - уже и выше. Величина , ближе к , чем значение единичного наблюдения, поскольку её случайная составляющая , есть среднее от чисто случайных составляющих в выборке и они как-бы «гасят» друг друга при расчёте среднего.

Вычтем из (1) (2):

, то есть оценка теоретической дисперсии зависит от (и только от) числа случайной составляющей наблюдений х в выборке. Поскольку эти составляющие меняются от выборки к выборке, так от выборки к выборке меняется и величина оценки .

Несмещённость.

Поскольку оценки являются случайными переменными, их значения лишь по случайному совпадению могут в точности равняться характеристикам генеральной совокупности. Обычно будет присутствовать определённая ошибка, которая может быть большой, или малой, положительной или отрицательной, в зависимости от чисто случайных составляющих величин х в выборке.

Желательно, чтобы оценка в среднем за достаточно длительный период была аккуратной. То есть математическое ожидание оценки = соответствующей характеристике генеральной совокупности. Такая оценка называется несмещённой. Если это не так, то оценка называется смещённой и разница, между её М. О. и соответствующей теоретической характеристикой генеральной совокупности называется смещением.

Полученная оценка – не единственно возможная несмещённая оценка . Рассмотрим выборку из всего двух наблюдений и . Любое взвешенное среднее наблюдений и было бы несмещённой оценкой, если сумма весов равна 1. Докажем, это. Рассмотрим обобщённую форму оценки:

,

то ,

z – несмещенная оценка.

Эффективность.

Несмещённость – желательное свойство оценок, но не единственное свойство. Ещё одна их важная сторона – это надёжность. Конечно, немаловажно, чтобы оценка была точной в среднем за длительный период. Пусть имеем две оценки теоретического среднего, рассчитанных на основе одной и той же информации. Поскольку функция плотности вероятности для В более «сжата», чем для А, с её помощью мы скорее получим более точное значение. Таким образом оценка В более эффективна. Эффективна та оценка, дисперсия которой min.

Противоречия между несмещённостью и минимальной дисперсией.

Для оценки желательна несмещённость и наименьшая возможная дисперсия. Эти критерии совершенно различны, и иногда они могут противоречить друг другу.

А – несмещённая

у В меньшая дисперсия.

Данный выбор зависит от обстоятельств. Если возможные ошибки вас не очень тревожат при условии, что за длительный период они «погасят» друг друга, то тогда выбираем А.

С другой стороны, если для вас приемлемы малые ошибки, но неприемлемы большие, то вам следует выбрать В.

Выбор определяется функцией потерь, стоимостью сделанной ошибки как функции её размера. Обычно выбирают оценку, дающую наименьшее ожидание потерь, и делается это путём взвешивания функции потерь по функции плотности вероятности.

Влияние увеличения размера выборки на точность оценок.

При увеличении n оценка становится более точной. В единичном эксперименте большая по размеру выборка необязательно даст более точную оценку, всегда может присутствовать элемент везения. Так как дисперсия , то она тем меньше, чем больше n.

Влияние увеличения размера выборки на распределение .

P = предел по вероятности.

Состоятельность.

Если предел по вероятности равен истинному значению характеристики генеральной совокупности, то эта оценка называется состоятельной. Таким образом, состоятельной называется такая оценка, которая даёт точное значение для большой выборки независимо от входящих в неё конкретных наблюдений.

Необходимо иметь в виду, что состоятельная оценка в принципе может на малых выборках работать хуже, чем состоятельная (иметь большее СКО) и поэтому требуется осторожность.