1.4 Способы вычисления вероятности

При решении последней задачи мы использовали данную величину вероятности попадания в цель при одном выстреле. Как определяется эта вероятность, будет показано в главе «Вероятность попадания и пора­жения цели».

Сейчас же рассмотрим общие принципы вычисления вероятности появления какого-либо события. В элементарном изложении их можно сгруппировать в следующие четыре способа.

а) Способ определения вероятности по вычисленной в результате опытов частоте события. Этот способ наиболее тесно связан с практикой, так как теория вероятностей изучает закономерности массовых случай­ных событий, обладающих устойчивой частотой. Рассмотренные выше свойства вероятности и примеры выявили соотношение вероятности и частоты события.

Стрелковая практика дает огромное число таких случайных собы­тий, которые обладают устойчивой частотой. Так, например, у одного и того же стрелка при многократном повторении одного упражнения число попаданий в цель (мишень) обычно изменяется незначительно; группа стрелков при многократном повторении одного и того же упражнения Курса стрельб дает процент выполнения, обычно, тоже довольно устой­чивый.

Сущность способа определения вероятности по частоте можно пока­зать на следующем примере.

В ходе тренировочных стрельб из пистолета на дальность 25 м по спортивной мишени № 5 сериями по 10 выстрелов одним из стрелков показаны следующие результаты (см. табл. 1).

Таблица № 1.

Результаты попаданий.

№№ серий	Результат стрельбы							Число попаданий в черный круг	Частота попаданий в черный круг
1	10x2	9x2	8x1	7x2	6x1	5x2	4x0	8	0,8
2	10x0	9x3 9х2	8x3	7x1	6x1	5x1	4x1	8	0,8
3	10х3 9х2		8x1	7x1	6x2 5x1		4x0	9	0,9
4	10x1	9x3	8x3	7x1	6x0	5x2	4x0	8	0,8
5	10x0	9x2	8x2	7x2	6x1	5x2	4x1	7	0,7
6	10x1	9x2	8x1	7x4	6x1	5x1	4x0	9	0,9
7	10x4	9x2	8x1	7x0	6x2	5x1	4x0	9	0,9
8	10x2	9x3	8x3	7x1	6x0	5x1	4x0	9	0,9
9	10x1	9x4	8x2	7x1	6x1	5х1	4x0	9	0,9
10	10x3	9x1	8x2	7x2	6x0	5x2	4x0	8	0,8

Из таблицы видно, что частота попадания в пределах круга 6 (в черный круг мишени) колеблется от 0,7 до 0,9. За вероятность попаданий этим стрелком в черный круг может быть принято среднее число 0,8. Тогда за вероятность промаха надо считать 0,2.

Чем больше было бы число проведенных опытов (в разбираемом нами примере - число серий), тем точнее была бы определена вероят­ность попадания в черный круг.

Вычисленная таким способом вероятность попадания не является верной для любого стрелка. Для начинающего, например, стрелка она будет, очевидно, меньшей, чем для мастера спорта. Следовательно, вы­числять вероятность попадания этим способом можно лишь для одного стрелка или для группы стрелков, имеющих примерно одинаковую под­готовку.

Рассмотренным способом вычисления вероятности события по часто­те его появления выработаны, например, нормы для определения кучно­сти отметок при наводке со станка на сокращенное расстояние (если точки отметок будут вмещаться в круг диаметром 3 мм - оценка кучно­сти «отлично» и т. д.); также выработаны оценки выполнения Курса стрельб для различных категорий стреляющих.

б) Способ определения вероятности по «отношению мер». Сущность этого способа объясним на следующем примере. Требуется определить вероятность попадания в грудную мишень, площадь которой 0,18 м². Пусть известно, что сердцевинные полосы рассеивания равны: Св = 0,7 м; Сб=0,6 м; мишень находится внутри сердцевины (рис. 5).

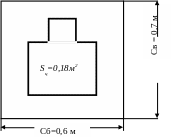
Р(Ф)=50%

Рис. 5. Вычисление вероятности по «отношению мер».

Чем больше площадь цели при данных условиях, тем больше пуль может попасть в мишень.

Считают приближенно, что внутри сердцевины рассеивание равномерно. Тогда в цель попадает во столько раз меньше пуль, чем в сердцевину, во сколько раз площадь цели меньше площади сердцевины.

Обозначим попадание в сердцеви­ну как событие А, попадание в цель - событие В. При условии, что вероят­ность попадания в сердцевину равна 0,5, вероятность попадания в цель равна

;

или 21,5%.

Определение вероятности попадания по способу «отношения мер» обосновывает применение так называемого коэффициента фигурности (Кф).

Кф - есть отношение площади мишени к площади описанного пря­моугольника. Понятно, что этот коэффициент можно применять лишь в том случае, когда рассеивание на площади прямоугольника можно счи­тать равномерным.

В общем случае для рассмотренного способа можно сказать, что если есть какая-то площадь, где частота события распределена равно­мерно и внутри этой площади находится вторая, где частота появления события пропорциональна её размерам, то вероятность события будет равна отношению размеров этих площадей.

Определение вероятности по «отношению мер» в стрелковой практи­ке применяется очень часто при решении задач на вероятность попада­ния и поражения цели.

в) Способ определения вероятности на основании подсчета равно­вероятных случаев. Этот способ основан на том, что вероятность появле­ния события равна отношению числа исходов испытания, благоприят­ствующих появлению интересующего нас события, к числу всех возмож­ных несовместных и равновероятных исходов события.

Как видно из определения, для применения этого способа необхо­димо убедиться в несовместности и равновероятности всех исхо­дов испытания. Это оказывается довольно сложно (особенно определе­ние равновероятности). Поэтому способ мало применим к решению за­дач в стрелковой практике, хотя в пособиях по стрельбе артиллерии и стрелковому делу он наиболее распространен для определения вероят­ности в примерах на шарах, кубиках, картах.

Пояснить определение вероятности по этому способу можно на сле­дующем примере. Предположим, в ящике находится пять одинаковых шаров, из которых два окрашены в красный цвет. Какова вероятность того, что вынутый на ощупь шар окажется красным?

В этом примере дано, что число исходов испытания, благоприят­ствующих появлению красного шара, равно двум. Число же всех возмож­ных несовместных событий при испытании равно пяти (равно числу всех шаров в ящике).

Вероятность того, что вынутый наугад шар окажется красного цве­та, равна отношению числа шансов, благоприятствующих появлению данного события, к числу всех равновероятных несовместных шансов, .

В этом примере легко можно убедиться в несовместности и равновероятности всех исходов испытания, т. к. в задаче было дано и общее число шаров, и число красных шаров. В большинстве же задач на опре­деление вероятности события из стрелковой практики это сделать очень трудно, а иногда и не представляется возможным. Как, например, под­считать, сколько шансов благоприятствует попаданию в цель при выст­реле? Понятно, что такие подсчеты неосуществимы и по этому способу вероятность попадания в цель определена быть не может.

Применяется этот способ в стрелковом деле при решении задач там, где приходится встречаться с равновероятными гипотезами (например, при обосновании правил стрельбы из орудий, минометов, пулеметов и т. д.).

г) Способ определения вероятности на основе известных вероятно­стей других событий. Этот способ можно объяснить на примере опреде­ления вероятности попадания хотя бы один раз при нескольких выстре­лах.

Пусть необходимо найти вероятность хотя бы одного попадания (P₁) при трех выстрелах, если известно, что вероятность попадания в цель при одном выстреле р=0,8.

При трех выстрелах из всех возможных исходов испытания нас не удовлетворяет сложное событие А, состоящее из трех промахов. Вероят­ность этого события Р(А) = (1-р)³ - по правилу умножения. Но сумма вероятностей событий, составляющих полную систему, равна 1. В нашем примере полную систему событий можно рассматривать как систему, состоящую из двух событий хотя бы одного попадания и двух про­махов.

Следовательно, вероятность хотя бы одного попадания P₁=1-Р(А), где Р(А) - вероятность трех промахов.

Итак, P₁ = 1-(1-р)³; Р₁= 1-(1-0,8)³ = 1-0,2³ = 0,992.

Очевидно, что при четырех выстрелах P₁ = 1 - (1-р)⁴, а при n выстре­лах

P₁=1-(1-р)ⁿ.

Эта формула показывает вероятность появления события хотя бы один раз при n испытаниях. Она же показывает вероятность поражения цели при n выстрелах, если для поражения достаточно одного попадания.

Так, вероятность поражения цели определена на основе известной вероятности другого события - вероятности попадания в цель при одном выстреле.

Все рассмотренные четыре способа определения вероятности приме­нимы к решению огневых задач. Как и когда применять каждый из них, надо решать, исходя из конкретных условий задачи.

Рассматривая способы определения вероятности, следует указать, что бывают случаи, когда вычисленная теоретически вероятность не оп­равдывается на практике. Например, расчетами может быть найдено, что вероятность попадания в мишень равна 0,9. Между тем, многочислен­ные стрельбы показывают, что в мишень попадает только 0,8 всех вы­пущенных пуль. Значит, вероятность высчитана неправильно, не учтены все причины, влияющие на ее величину. Так, очень часто, рассчитывая вероятность попадания, не учитывают ошибки в прицеливании, вид огня (одиночный, короткими или длинными очередями и т. д.), положение стрелка при стрельбе и т. п. и получают, поэтому неверный результат.

Влияние указанных причин на вероятность попадания теоретически еще изучено не полностью. Поэтому нельзя обосновывать условия упраж­нений Курса стрельб только знанием величин табличного рассеивания. Условия этих упражнений выработаны многолетней практикой и много­численными опытными стрельбами.

Практика (опыт) всегда показывает правильность или неправиль­ность теоретических расчетов, подсказывает новые пути решения, ста­вит новые вопросы. Так, в последние годы практика поставила перед теорией задачу исследования вопросов влияния на вероятность попада­ния длины очереди при стрельбе автоматическим огнем, ошибок в прице­ливании, положении для стрельбы и ряд других вопросов рассеивания при стрельбе автоматическим огнем.

В заключение рассмотрения способов расчета вероятности приведем примеры задач на определение вероятности появления событий.

Пример 1. Вероятность попадания в окоп гранатой АГС-17 при одном выстреле р=0,1. Какова вероятность хотя бы одного попадания в цель при четырех выстрелах?

Решение. Р₁=1-(1-р)ⁿ; Р₁ =1-(1-0,1)⁴; Р₁ = 0,3439 или примерно 34%.

Пример 2. Две БМП-2 ведут одновременно огонь по БЗО против­ника. Вероятность попадания в цель из первого БМП-2 p₁=0,2; из второ­го - р₂=0,4. Какова вероятность поражения цели, если БМП-2 произведут по одному выстрелу? (Для поражения цели достаточно одного попа­дания).

Решение, Р₁ =1-q₁ ·q₂, где q₁ - вероятность промаха 1-го БМП-2, равная 0,8; q₂ - вероятность промаха 2-гo БМП-2 равная 0,6.

Р₁ =1-0,8·0,6 =1-0,48 =0,52 или 52%.

Пример 3. При стрельбе из пистолета по мишени № 5 (спортивной) для данного стрелка попадание в черный круг достоверно. Какова веро­ятность того, что при одном выстреле он выбьет не менее 8 очков, если вероятности выбить 10, 9, 7, 6 очков соответственно равны: Р(10)=0,15; Р(9) =0,25; Р(7) =0,2; Р(6) =0,2.

Решение. 1) Вероятность попадания в восьмерку равна

Р(8)=1-[Р(10)+Р(9)+Р(7)+Р(6)];

Р(8) =1-(0,15+0,25+0,20+0,20)=1-0,8=0,2.

2) Вероятность выбить не менее 8 очков равна сумме вероятностей

Р(10)+Р(9)+Р(8), т. е. 0,15+0,25+0,20=0,6 или 60%.