- •Раздел . Интегральное исчисление
- •1. Неопределённый интеграл Первообразная
- •Неопределённый интеграл и его свойства
- •Основные методы интегрирования
- •1. Непосредственное интегрирование (метод разложения).
- •2. Метод замены переменной
- •Метод интегрирования по частям
- •4. Интегрирование рациональных выражений Дробно-рационалъные функции.
- •Раздел . Интегральное исчисление
- •1. Определённый интеграл Задачи, приводящие к понятию определённого интеграла
- •Определённый интеграл как предел интегральной суммы
- •Основные свойства определённого интеграла
- •Формула Ньютона – Лейбница
- •Вычисление определенного интеграла
Определённый интеграл как предел интегральной суммы
Обобщим рассуждения, проведенные при решении двух предыдущих задач о массе прямолинейного стержня и о площади криволинейной трапеции.
П







y
x
y = f(x)
f(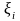 )
)
0
a
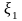
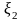 ……
……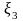 ………
……… b
b
 .
Через
.
Через
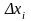 обозначим разность, которую условимся
называть длиной частичного отрезка
[xi-1,
xi].
обозначим разность, которую условимся
называть длиной частичного отрезка
[xi-1,
xi].
Рис. 3.
Образуем
сумму
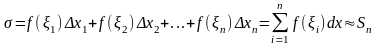 которую назовем
интегральной суммой для функции
f(x)
на [a,b]
соответствующей данному разбиению
[a,b]
на частичные отрезки и данному выбору
промежуточных точек
которую назовем
интегральной суммой для функции
f(x)
на [a,b]
соответствующей данному разбиению
[a,b]
на частичные отрезки и данному выбору
промежуточных точек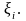
Определение
1.
Функция
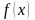 интегрируема на промежутке
,
если при любых разбиениях
интегрируема на промежутке
,
если при любых разбиениях
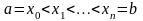 промежутка
,
таких, что
промежутка
,
таких, что
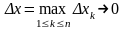 при произвольном выборе точек
при произвольном выборе точек
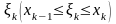 ,
сумма
,
сумма
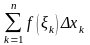 при
при
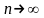 стремится к пределу S.
стремится к пределу S.
Предел
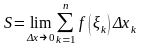 называют определенным интегралом
от функции
на промежутке
и обозначают
называют определенным интегралом
от функции
на промежутке
и обозначают
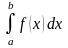 ,
т.е.
,
т.е.
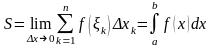
(2)
.Число a называется нижним пределом интеграла, b- верхним.
Промежуток называется промежутком интегрирования, x- переменной интегрирования.
Теорема 1. Если функция непрерывна на ,то интеграл существует.
Площадь
криволинейной трапеции, ограниченной
кривой
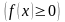 ,
прямыми
,
прямыми
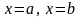 и осью x, вычисляется
с помощью интеграла
и осью x, вычисляется
с помощью интеграла
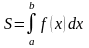 .
.
Определение
1. Если существует конечный предел
интегральной суммы (1) при
 ,
то этот предел называется определенным
интегралом от функции f(x)
по отрезку [a,b]
и обозначается следующим образом:
,
то этот предел называется определенным
интегралом от функции f(x)
по отрезку [a,b]
и обозначается следующим образом:
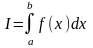 или
или
Основные свойства определённого интеграла
Пусть
дан интеграл

1.
Если
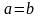 ,
то
,
то
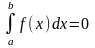 (по определению).
(по определению).
2.
Если
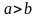 ,
то по определению
,
то по определению
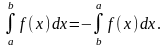
3.
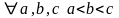
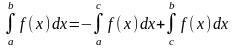
4.
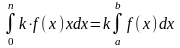
5.
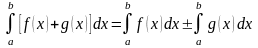
Формула Ньютона – Лейбница
(Основная формула интегрального исчисления)
Выведем
формулу для вычисления определенного
интеграла. Каждая из первообразных,
например F(x), для функции y = f(x)
отличается от первообразной Ф(х)
=
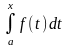 постоянным слагаемым
постоянным слагаемым
Ф(х) = F(x) + C.
Для нахождения значения С положим в последнем равенстве x = a.
Тогда
Ф(а)
=
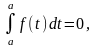 или F(a) + C = 0, откуда C
= - F(a).
или F(a) + C = 0, откуда C
= - F(a).
Значит, Ф(х) = F(x) - F(a).
При x=b
Ф(b)
=

Формула получила название формулы Ньютона – Лейбница.
Вычисление определенного интеграла
Вычисление
определенного интеграла
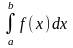 выполняется следующим образом, находим:
выполняется следующим образом, находим:
1)
неопределенный интеграл
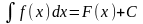 ;
;
2)
значение интеграла
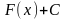 при
при
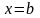 ,
т. е. вычисляем
,
т. е. вычисляем
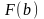 ;
;
3)
значение интеграла
при
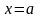 ,
т. е. вычисляем
,
т. е. вычисляем
 ;
;
4)
разность
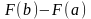 .
.
Процесс вычисления виден из формулы
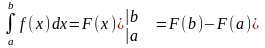 .
(6)
.
(6)
При вычислении определенного интеграла применяются следующие свойства определенного интеграла:
1) при перестановке пределов интегрирования знак определенного интеграла меняется на противоположный;
2) постоянный множитель подынтегрального выражения можно выносить за знак определенного интеграла:
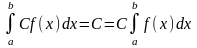 ;
(7)
;
(7)
3) определённой интеграл алгебраической суммы функций равен алгебраической сумме определённых интегралов этих функций:
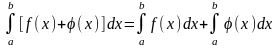 (8)
(8)
Пример
1. Вычислить интеграл
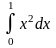
Пример
2. Вычислить
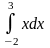 .
.
Пример
3. Вычислить
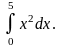
Пример
4. Вычислить определённый
интеграл
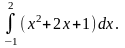
Пример
5. Вычислить
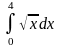 .
.
Пример
6.
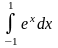 .
.
Пример
7.
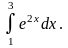
Пример
8.
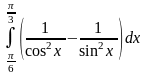 .
.
Пример 9. Вычислить площадь, ограниченную графиком функции у = х3, осью х и прямыми х = 1 и х = 3 (рис. 7)
Замена переменной и формула интегрирование по частям
в определённом интеграле
Замена переменной
Пример
1.
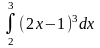
Пример
2.
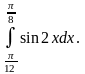
Пример
3.
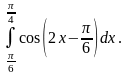
Пример
4.
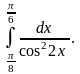
Интегрирование по частям
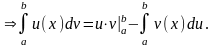
Пример
1. Найти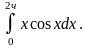
Пример
2. Вычислить
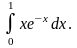
Пример
3. Вычислите
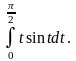
Вычисление площадей плоских фигур.
Определение определенного интеграла как предела интегральной суммы позволяет получить различные формулы для нахождения площадей, длин и объемов геометрических объектов.
П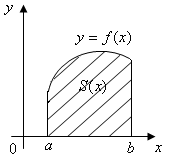 усть
дана функция
усть
дана функция
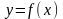 ,
,
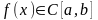 ,
,
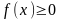 .
Рассмотрим определенный интеграл от
этой функции. С геометрической точки
зрения определенный интеграл – это
площадь под кривой
.
Рассмотрим определенный интеграл от
этой функции. С геометрической точки
зрения определенный интеграл – это
площадь под кривой
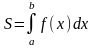 .
(11)
.
(11)
Рис.1.
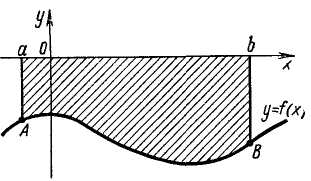
Площадь
S находится по формуле:
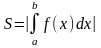 или
или
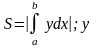 находится из уравнения кривой.
находится из уравнения кривой.
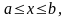
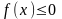 )
и двумя прямыми x =
a и x
= b (рис.2).
)
и двумя прямыми x =
a и x
= b (рис.2).
Рис. 2.
Пусть функция принимает как положительные, так и отрицательные значения, тогда площадь можно найти по формуле:
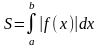 (12)
(12)
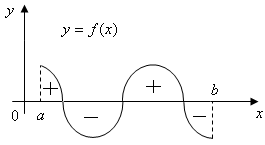
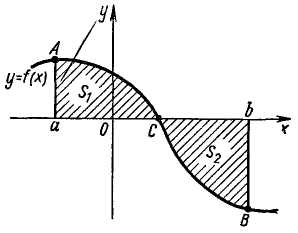
Рис. 2.
Пусть
дана функция
,
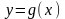 ,
где
,
где
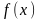 ,
,
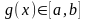 ,
,
,
,
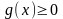 .
Тогда площадь ограниченная этими линиями
определяется по формуле
.
Тогда площадь ограниченная этими линиями
определяется по формуле
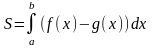 ,
(13)
,
(13)
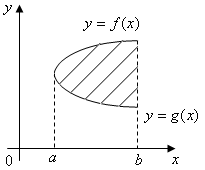
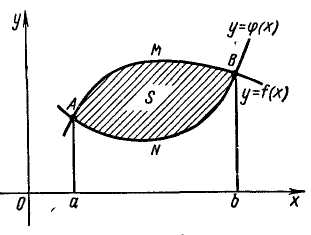
Рис. 5
Рис. 4.
Пример 1. Вычислить площадь, ограниченную графиками функций: