
- •Раздел . Интегральное исчисление
- •1. Неопределённый интеграл Первообразная
- •Неопределённый интеграл и его свойства
- •Основные методы интегрирования
- •1. Непосредственное интегрирование (метод разложения).
- •2. Метод замены переменной
- •Метод интегрирования по частям
- •4. Интегрирование рациональных выражений Дробно-рационалъные функции.
- •Раздел . Интегральное исчисление
- •1. Определённый интеграл Задачи, приводящие к понятию определённого интеграла
- •Определённый интеграл как предел интегральной суммы
- •Основные свойства определённого интеграла
- •Формула Ньютона – Лейбница
- •Вычисление определенного интеграла
2. Метод замены переменной
Этот метод называют также методом подстановки. Он является одним из наиболее эффектных и распространенных примеров интегрирования, позволяющих во многих случаях упростить вычисления интеграла.
Пусть требуется найти интеграл
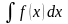
первообразная которого неизвестна, но известно что она существует. В этом случае можно попытаться сделать такую замену переменной, чтобы интеграл стая табличным. Для обоснования такого подхода к интегрированию рассмотрим теорему.
Пример
1. Найти
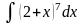 .
.
Пример
2.
Найти интеграл
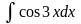 .
.
Пример
3. Найти интеграл
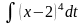
Метод замены переменных является одним из основных методов вычисления неопределенных интегралов. Даже в тех случаях, когда мы интегрируем каким либо другим методом, нам часто приходится в промежуточных вычислениях прибегать к замене переменных. Успех интегрирования зависит в значительной степени от того, сумеем ли мы подобрать такую удачную замену переменных, которая упростила бы данный интеграл. По существу говоря, изучение методов интегрирования сводится к выяснению того, какую надо сделать замену переменной при том или ином виде подынтегрального выражения.
Метод интегрирования по частям
Пусть
функции
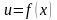 и
и
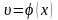 непрерывно дифференцируемые на некотором
интервале. Имеет место тождество:
непрерывно дифференцируемые на некотором
интервале. Имеет место тождество:
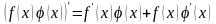 .
.
Известно, что дифференциал произведения двух функций u(x), v(x) вычисляются по формуле:
d (uv) = udv + vdu
Интегрируя
обе части, получим формулу интегрирования
по частям
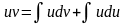 или
или
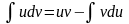 Эта формула
называется формулой интегрирования по
частям.
Эта формула
называется формулой интегрирования по
частям.
Пример
1. Найти интеграл
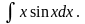
Пример
2. Вычислить интеграл
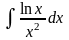 .
.
4. Интегрирование рациональных выражений Дробно-рационалъные функции.
Определение
1.Функция вида
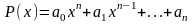 ,
,
где
,
 ,
,
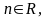 a0,a1,...tan
любые числа,
a0,a1,...tan
любые числа,
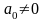 называется целой
рациональной функцией.
называется целой
рациональной функцией.
Определение 2. Функция являющаяся частным двух целых рациональных функций называется дробно-рациональной функцией
R(x)
=
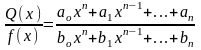
Если т<n, дробь называется правильной, если т>n дробь называется неправильной.
Пусть n< m дробь неправильная, тогда разделив числитель на знаменатель, получим
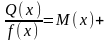
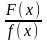 ,
,
где М(х) – многочлен, а - правильная дробь.
Пример
1. Представить
неправильную дробно- рациональное
выражение
 в виде правильной дроби.
в виде правильной дроби.
Раздел . Интегральное исчисление
1. Определённый интеграл Задачи, приводящие к понятию определённого интеграла
Многие задачи естествознания и техники получили решение благодаря одному из основных понятий математического анализа - определенному интегралу. Нахождение площадей, ограниченных кривыми, длин дуг, объемов, работы, пути, скорости, моментов инерции и т.д., сводится к его вычислению. Рассмотрим некоторые задачи, приводящие к понятию определенного интеграла.
Задача
о площади криволинейной трапеции.
Дана плоская фигура, ограниченная
графиком функции
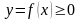 и отрезками прямых
и отрезками прямых
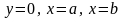 .
Функция
.
Функция
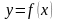 определена, непрерывна и неотрицательна
в промежутке
определена, непрерывна и неотрицательна
в промежутке
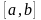 .
Вычислить площадь S
полученной фигуры
.
Вычислить площадь S
полученной фигуры
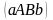 ,
называется криволинейной трапецией.
,
называется криволинейной трапецией.
