Глава 1

Вписанные и описанные многоугольники

43

Теорема 3 (о точке пересечения серединных перпендику­ляров к сторонам треугольника). Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

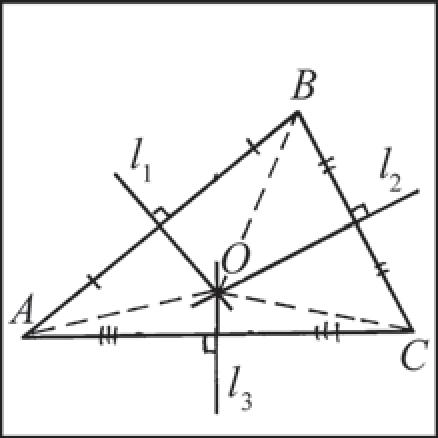
Д о к а з а т е л ь с т в о. Пусть l₁, l₂ и l₃ — серединные перпенди­куляры к сторонам AB, BC и AC треугольни­ка ABC соответственно (рис. 38). Докажем что серединные перпендикуляры l₁, l₂ и l₃ пересекаются в одной точке.

Рис. 38

1) Обозначим буквой O точку пересе­чения серединных перпендикуляров l₁ и l₂. То г д а по теореме о серединном перпендику­ляре справедливы равенства OA = OB (так как l₁ — серединный перпендикуляр к отрезку AB) и OB = OC (так как l₂ — серединный перпендикуляр к отрезку BC). Отсюда следует, что OA = OC.

2) Равенство OA = OC означает, что точка O равноудалена от вершин A и C. Значит, по теореме о серединном перпендикуляре точка O лежит на серединном перпендикуляре к стороне AC . Таким образом, все три серединных перпендикуляра l₁, l₂ и l₃ пересекаются в одной точке.

Теорема доказана.

Воспользуемся данной теоремой для доказательства свойства высот треугольника.

Те о р е м а 4 (о точке пересечения прямых, на которых лежат высоты треугольника). Прямые, на которых лежат высоты треугольника, пересекаются в одной точке.

уГ		В	F
	5к	tyy
л V^		ус
D

Д о к а з а т е л ь с т в о.

Рис. 39

1. Пусть ABC — произвольный тре­угольник и AA₁, BB₁ и CC₁ — его высоты (рис. 39). Докажем, что прямые, содержа­щие высоты треугольника, пересекаются в одной точке.

2. Проведем через вершины A, B и C прямые, параллельные соответственно сто­ронам BC, A C и AB. Пусть T, F и D — точки их пересечения.

Скачено с Образовательного

3. Докажем, что точки Л, 5 и С являются соответственно сере­динами сторон TD, TF и /Ю треугольника TFD. Например, докажем, что точка С — середина стороны DF. Так как четырехугольник ABCD — параллелограмм, то АВ = DC. Так как ABFC параллелограмм, то АВ = CF. Таким образом, DC = СF.

4. Аналогично доказывается, что AT = AD и TB = BF. По усло­вию АА₁ _LfiC, а по построению TD || ВС, следовательно, АА₁ _l_ TD. Аналогично, ВВ₁ _l_ TF и СС₁ _LZ)/\ Значит, прямые АА₁, ВВ₁ и СС₁ являются серединными перпендикулярами к сторонам треугольника TFD. Следовательно, они пересекаются в одной точке.

Теорема доказана.

Точка пересечения медиан, точка пересечения биссектрис и точка пересечения высот называются замечательными точками треугольника.

Заметим, что если треугольник остроугольный, то пересекаются в одной точке сами его высоты, а если треугольник тупоугольный, то пересекаются в одной точке прямые, на которых лежат высоты.