Основы исчисления высказываний
3.1.1. Основные определения
Определение. Под простым (элементарным) высказыванием будем понимать простое повествовательное предложение, которое может быть либо истинным, либо ложным.
Простые высказывания будем обозначать буквами латинского алфавита, прописными или строчными, быть может, с индексами. Как только простое высказывание получит такое буквенное обозначение, мы отождествим его с логической переменной из раздела II, которая может принимать одно из двух значений − И (истина) или Л (ложь). Буквы И и Л удобно заменять цифрами 1 и 0 соответственно, в дальнейшем, в основном, будем пользоваться цифровыми обозначениями. Но противоречие, формулу, тождественно равную 0, и тавтологию, формулу, тождественно равную 1, мы будем обозначать как символами 0 и 1, так и символами Л и И.
Из простых высказываний посредством логических связок составляются сложные высказывания. Логических связок всего пять: отрицание («не»), дизъюнкция («или»), конъюнкция («и», «а»), импликация («если то»), эквивалентность (эквивалентно», «тогда и только тогда»).
Эти пять логических
связок обозначаются символами ‾,
соответственно. Получив такое обозначение,
они отождествляются с пятью основным
логическим функциям из раздела II.
А всякое сложное высказывание, записанное как последовательность символов, состоящую из имен переменных, соединенных логическими связками, превращается в логическую формулу из раздела II.
Напомним правила составления формул.
Всякая переменная, быть может с индексами, это формула. Логические константы 0 и 1 это формулы.
Если
формула, то
и
это формулы.Если
и
формулы, то
,
− это формулы.Других формул нет.
По-прежнему, для
облегчения чтения, мы не будем использовать
символ &, предпочитая обозначать
конъюнкцию просто
.
Все, что говорилось о формулах в разделе II, полностью переносится в исчисление высказываний. В частности, для всякой формулы можно построить таблицу истинности, формулы можно преобразовывать в равносильные, всякую формулу можно преобразовать в ДНФ и КНФ, сохраняются правила вычисления значений формулы.
В исчислении
высказываний всякий набор значений
переменных формулы принято называть
ее интерпретацией.
Так что у всякой формулы, зависящей от
переменных
интерпретаций.
Тождественно истинная формула, равная 1 на всякой интерпретации, называется тавтологией и обозначается 1. Тождественно ложная формула, равная 0 на всякой интерпретации, называется противоречием и обозначается 0.
А теперь приведем примеры записи сложных высказываний формулами.
Записать формулами следующие высказывания.
Если верно, что, когда идет дождь, дороги мокрые, то также верно, что если дороги сухие, то дождя нет.
Он сказал, что придет, если будет хорошая погода.
Если будет сильный ветер, мы не пойдем на каток, а отправимся в музей.
Петров поедет либо в Москву, либо в Кострому, но не в оба города.
Если допоздна работать с компьютером и при этом пить много кофе, то утром просыпаешься в дурном расположении духа или с головной болью.
Он счастлив, если управляет автомобилем. Он счастлив, только если управляет автомобилем. Он счастлив тогда и только тогда, когда управляет автомобилем.
Решение.
Положим
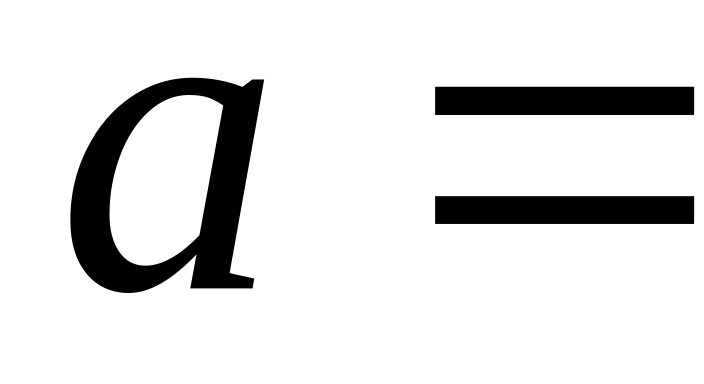«идет дождь»;
«дороги мокрые».
Тогда
.
В самом деле, импликация
выражает высказывание «если идет дождь,
то дороги мокрые»; импликация
соответствует высказыванию «если дороги
сухие, дождя нет» Эти импликации −
посылка и заключение импликации
высказывания 1.
А теперь преобразуем
формулу
,
используя известные равносильности.
.
Формула − это тавтология, тождественно истинная формула.
Составим также и таблицу истинности формулы (табл. 1).
Таблица 1
|
|
|
|
|
|
|
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
Если не раскрывать содержание высказываний и , то прочитать формулу можно так: «если верно, что из истинности следует истинность , то также верно, что из ложности следует ложность ». Мы показали, что такая формула остается логически истинной, если заменить в ней буквы и любыми высказываниями.
Пусть
«он придет»;
«будет хорошая погода». Тогда
.Обозначим: «будет сильный ветер»; «мы пойдем на каток»;
«мы отправимся в музей». Данное
высказывание записывается формулой
.
Знак конъюнкции не указан из соображений
лучшего чтения формулы.Если «Петров поедет в Москву»; «Петров поедет в Кострому», то данное утверждение передается формулой
,
ведь поездки взаимно исключают друг
друга.В этом примере обе возможности (как проснуться в дурном расположении духа, так и проснуться с головной болью) совместимы, к сожалению. Тогда если
«мне пришлось допоздна работать с
компьютером»,
«я проснулся утром в дурном расположении
духа»;
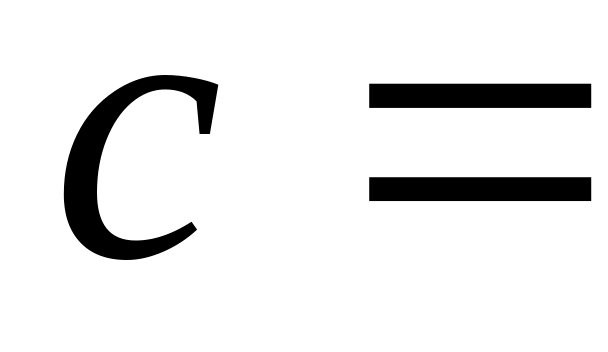«я проснулся утром с головной болью»,
то
.Пусть «он счастлив»; «он управляет автомобилем». В этом примере сформулированы три утверждения, выражающие соответственно достаточные, необходимые, необходимые и достаточные условия истинности некоторого события. Рассмотрим каждое из них.
В утверждении «он
счастлив, если управляет автомобилем»
сформулированы достаточные условия
счастья этого человека. Если он управляет
автомобилем, он наверняка счастлив, что
не исключает возможности ему быть
счастливым не только за рулем. Первое
утверждение записывается формулой
.
Преобразуем импликацию в равносильную
формулу.
.
Итак, если он несчастлив, он наверняка
не управляет автомобилем.
Высказывание «он
счастлив, только если управляет
автомобилем», означает необходимые
условия счастья. Если этот человек
счастлив, он, безусловно, за рулем. В
ином состоянии он всегда несчастлив.
Кроме того, управление автомобилем еще
не гарантирует счастье, все может быть.
Поэтому данное высказывание записывается
формулой
.
Наконец, в последнем
высказывании сформулированы необходимые
и достаточные условия его счастья. Он
счастлив, если и только если управляет
автомобилем. Следовательно, нужно
записать формулу
.
Пример преобразования формулы.
Рассмотрим следующее
высказывание: «если
и
невиновны, то
несомненно виновен. Допустим, что это
ложь. Какова же истина?
Решение.
Положим
«
виновен»,
«
виновен»,
«
виновен». Тогда исходное высказывание
записывается формулой
.
Если
,
то
.
Итак, все трое невиновны!