
Задание 3
Вычислить неопределенный интеграл |
||||
3.1. |
|
|
3.6. |
|
3.2. |
|
|
3.7. |
|
3.3. |
|
|
3.8. |
|
3.4. |
|
|
3.9. |
|
3.5. |
|
|
3.10. |
|
Интегрирование рациональной функции после выделения целой части сводится к интегрированию правильной рациональной дроби
![]()
где
![]() и
и
![]() - целые многочлены, причем степень
числителя
ниже степени знаменателя
.
Если
- целые многочлены, причем степень
числителя
ниже степени знаменателя
.
Если
![]()
где
![]() - различные действительные корни
многочлена
;
- различные действительные корни
многочлена
;
![]() - натуральные числа (кратности корней),
то справедливо разложение дроби
- натуральные числа (кратности корней),
то справедливо разложение дроби
![]() на простейшие
дроби:
на простейшие
дроби:
![]()
Для
вычисления неопределенных коэффициентов
![]() обе части тождества приводят к целому
виду, а затем приравнивают коэффициенты
при одинаковых степенях переменной
.
Можно также определять эти коэффициенты,
полагая в тождестве
равным подходяще подобранным числам.
обе части тождества приводят к целому
виду, а затем приравнивают коэффициенты
при одинаковых степенях переменной
.
Можно также определять эти коэффициенты,
полагая в тождестве
равным подходяще подобранным числам.
Пример 3. Вычислить неопределенный интеграл
![]()
Решение
Применим метод неопределенных коэффициентов. Так как подынтегральная функция есть правильная рациональная дробь (степень многочлена в числителе меньше степени многочлена в знаменателе), то приступим сразу к нахождению неопределенных коэффициентов. Для этого представим подынтегральную функцию в виде
![]()
Приведем выражение в правой части к общему знаменателю
![]()
![]()
Из равенства дробей следует равенство многочленов
![]()
Приравнивая
коэффициенты при одинаковых степенях
,
получаем систему для определения
неизвестных
![]() и
и
![]() :
:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ,
,
решая
которую, находим
![]()
Теперь мы можем представить подынтегральную функцию в виде суммы правильных рациональных дробей:
![]()
Следовательно:
![]()
![]() .
Первые четыре интеграла сводятся к
табличным
.
Первые четыре интеграла сводятся к
табличным
![]()
![]()
Для нахождения последнего интеграла воспользуемся рекуррентной формулой:
если
![]() ,
то
,
то
![]()
При
![]() интеграл
интеграл
![]() - табличный. Тогда
- табличный. Тогда
![]()
![]()
![]()
![]()
Ответ:
![]()
Задание 4
-
Вычислить неопределенный интеграл
4.1.
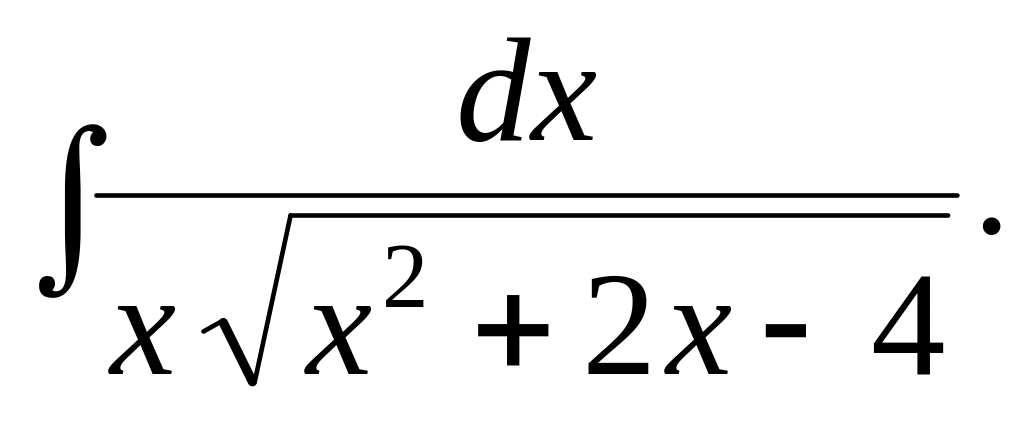
4.6.
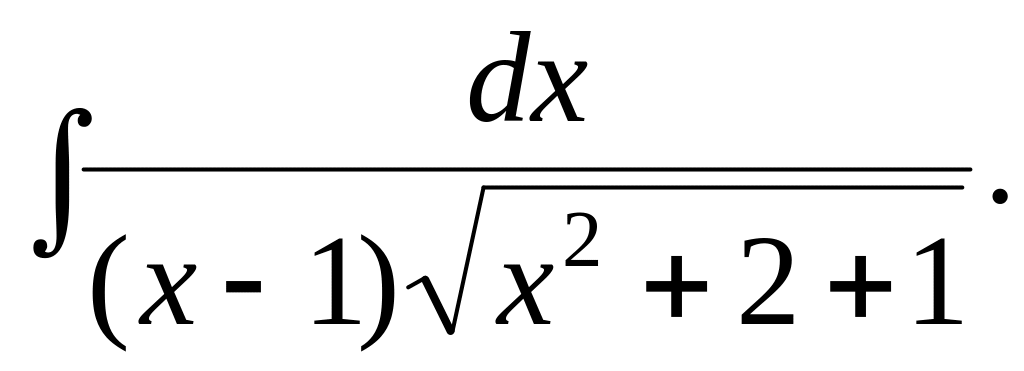
4.2.

4.7.
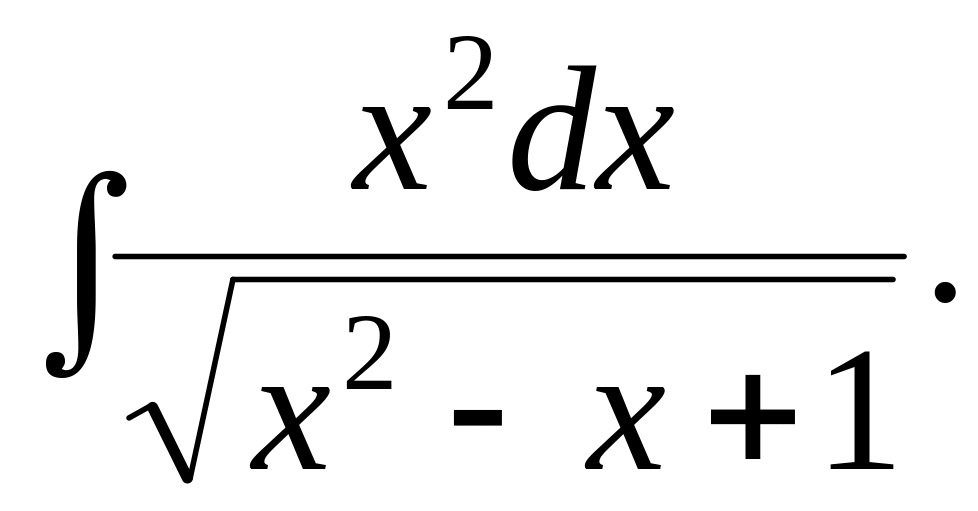
4.3.
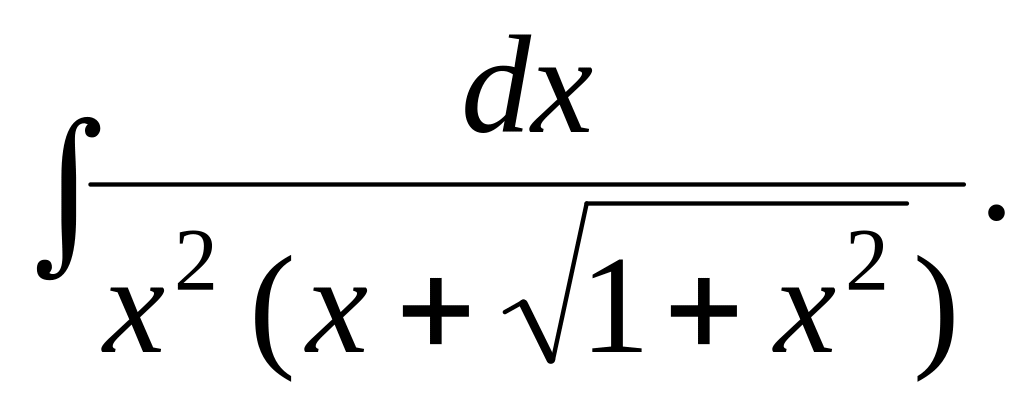
4.8.

4.4.
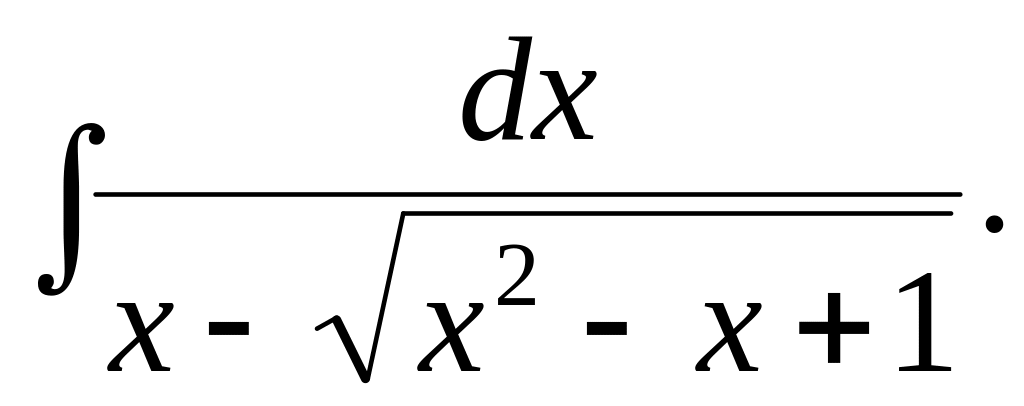
4.9.
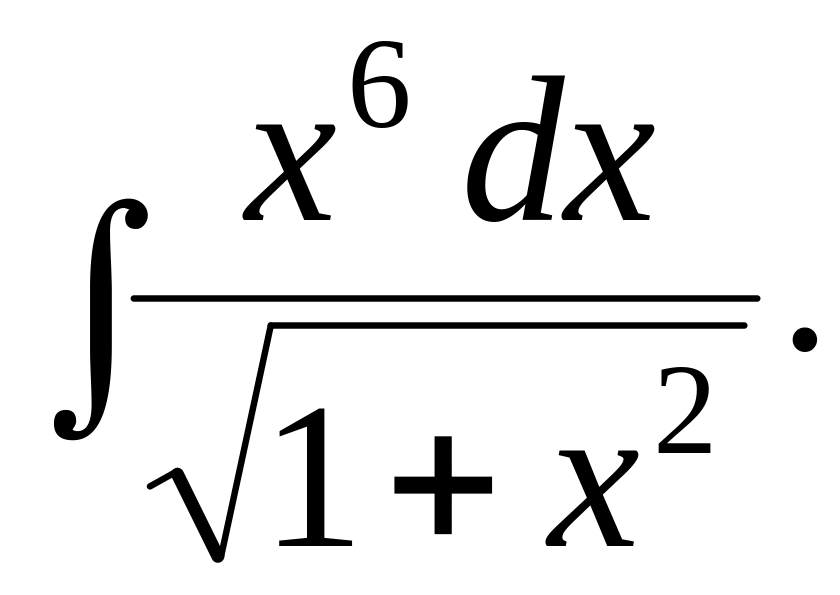
4.5.
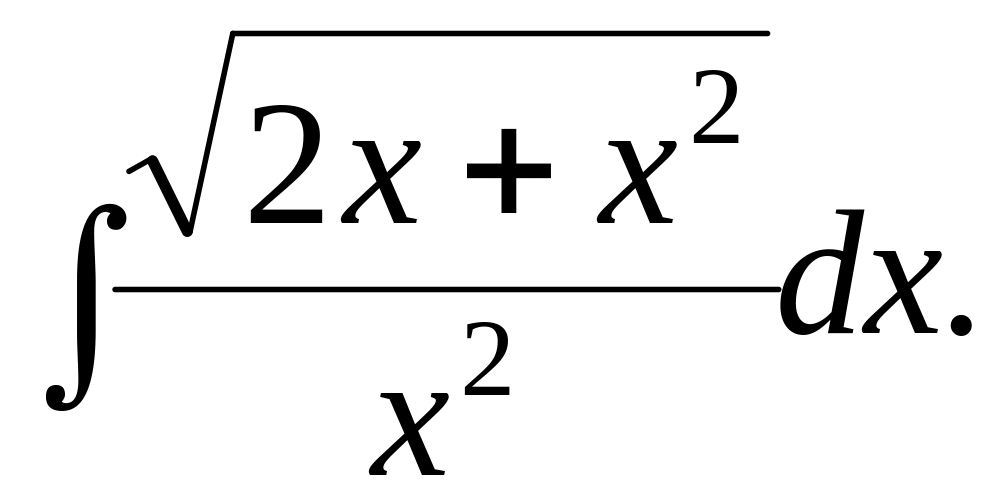
4.10.
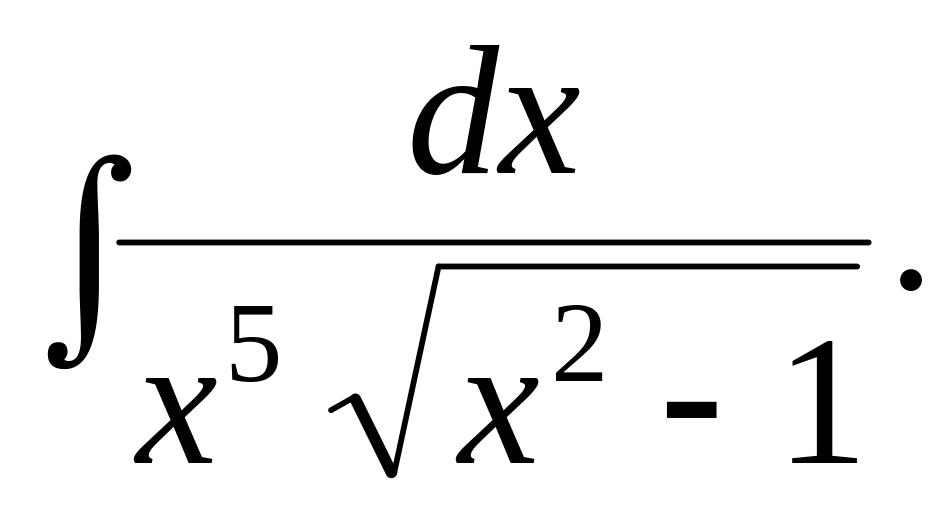
Пример 4. Вычислить неопределенные интегралы:
a)
![]() б)
б)
![]() в)
в)
![]()
Решение
а)
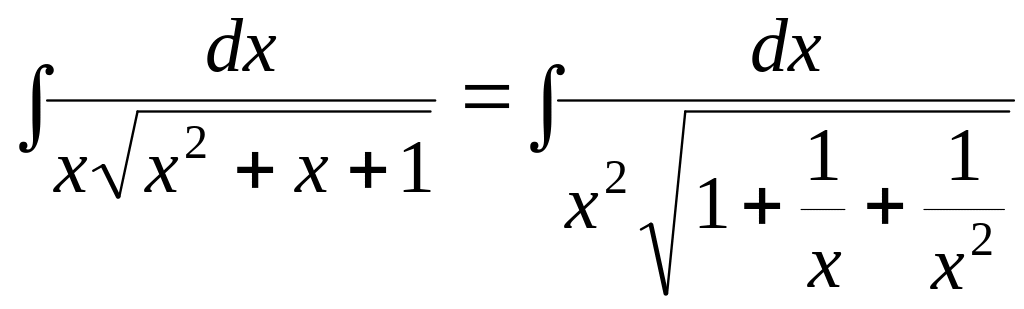 .
Обозначим
.
Обозначим
![]()
Отсюда
![]() .
Тогда интеграл примет вид
.
Тогда интеграл примет вид
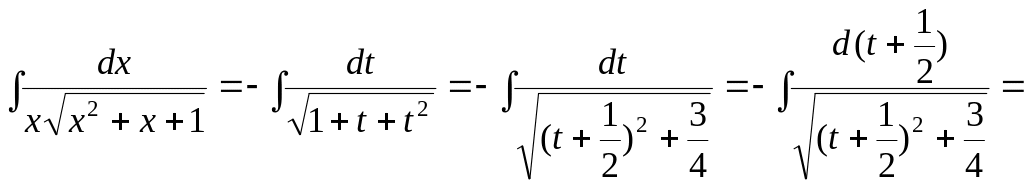
![]()
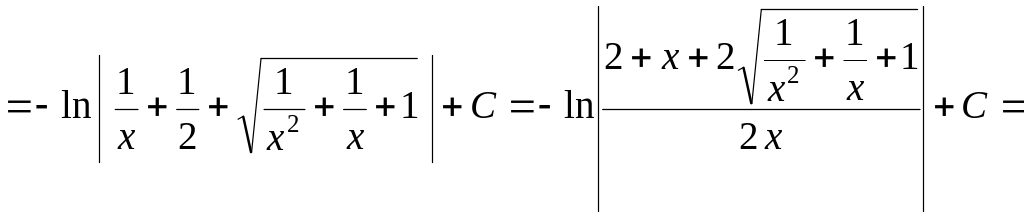
![]()
Ответ:
![]() ;
;
б)
в данном интеграле сделаем подстановку
![]() Отсюда
Отсюда
![]() при
этом
при
этом
![]() Исходный интеграл примет вид
Исходный интеграл примет вид
![]()
![]() Разложим
подынтегральную функцию в виде
Разложим
подынтегральную функцию в виде
![]() .
Коэффициенты
.
Коэффициенты
![]() и
найдем, используя метод неопределенных
коэффициентов (см. пример
3):
и
найдем, используя метод неопределенных
коэффициентов (см. пример
3):
![]()
Таким образом:
![]()
![]() где
где
![]()
Ответ:
![]() где
где
![]() ;
;
в) перепишем данный интеграл в виде
![]()
В общем случае интеграл
![]()
(где
![]() и
и
![]() - рациональные числа) называется
интегралом от дифференциального бинома,
который может быть приведен к
интегрированию рациональных функций
в трех случаях:
- рациональные числа) называется
интегралом от дифференциального бинома,
который может быть приведен к
интегрированию рациональных функций
в трех случаях:
Пусть - целое. Полагаем
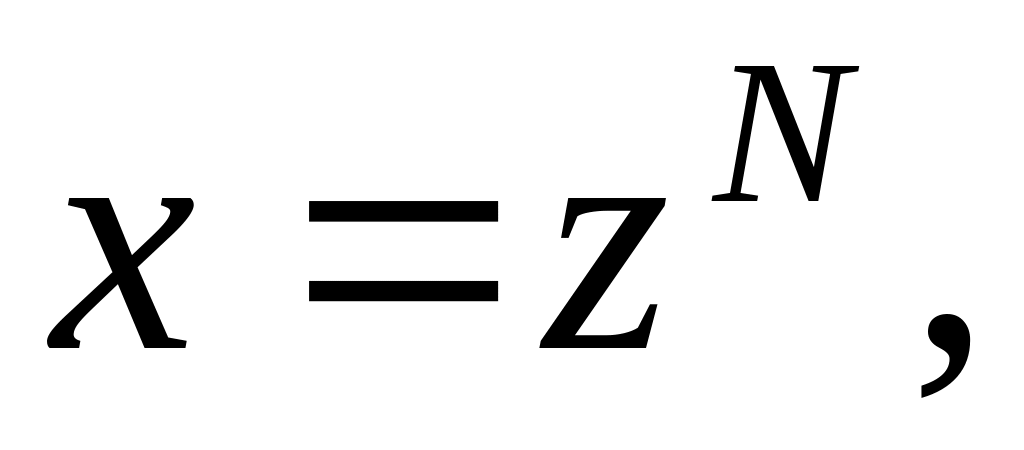 где
где
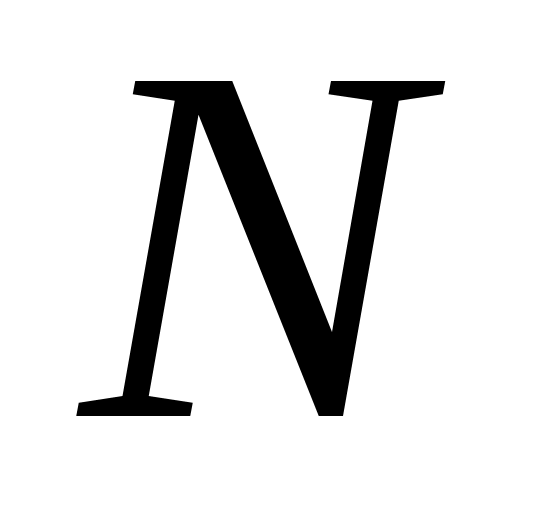 - общий знаменатель дробей
- общий знаменатель дробей
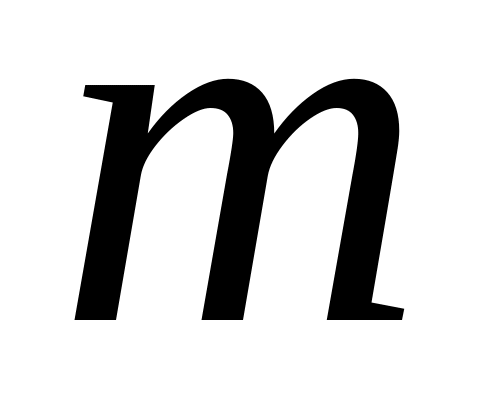 и
и
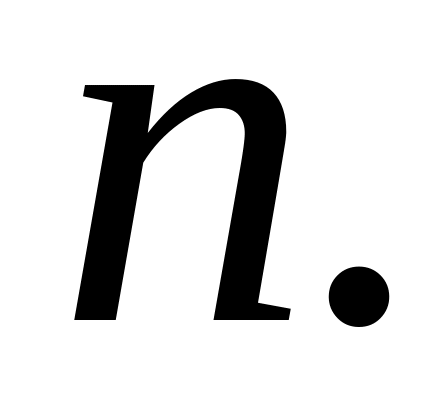
Пусть
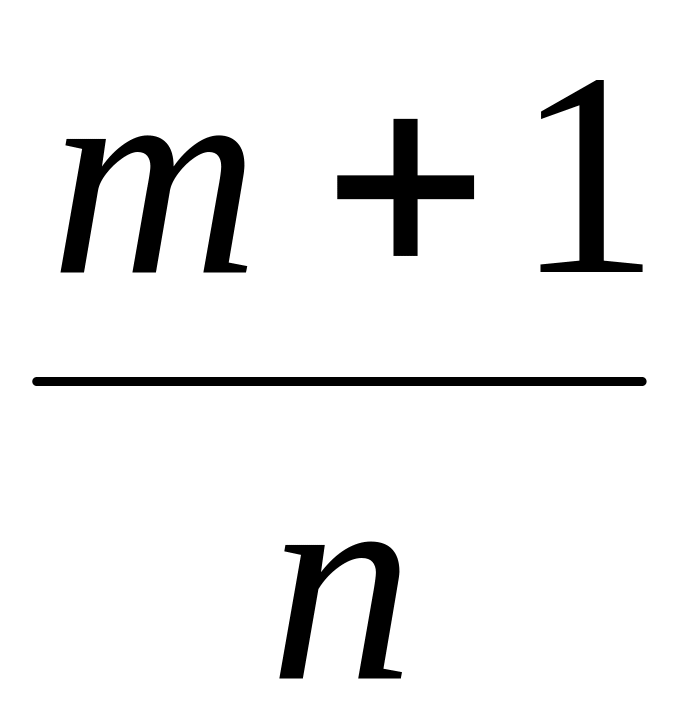 - целое. Полагаем
- целое. Полагаем
 где
-
знаменатель дроби
где
-
знаменатель дроби
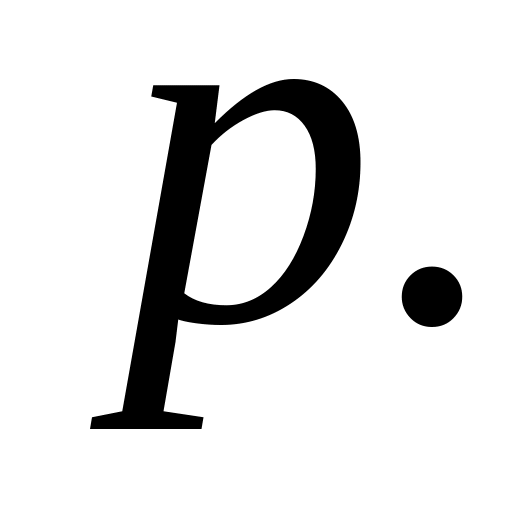
Пусть
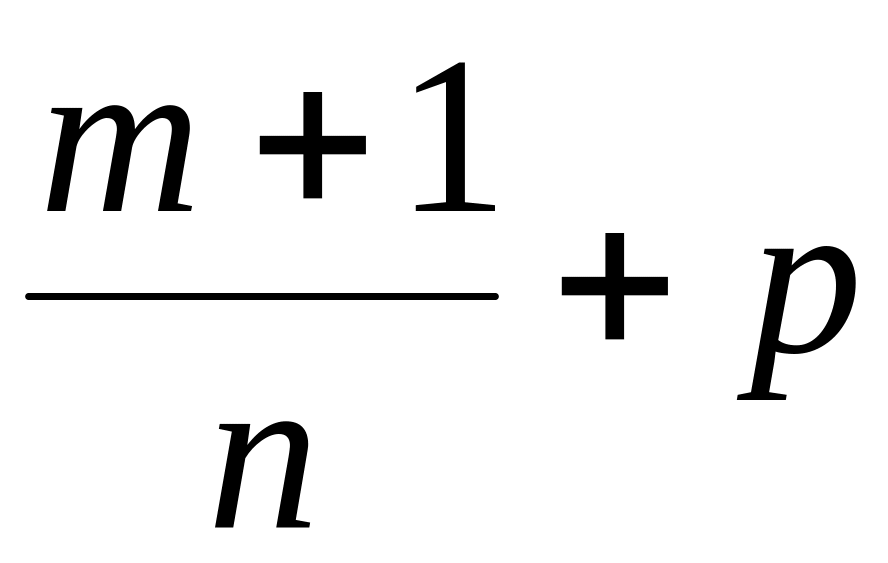 – целое. Применяем подстановку
– целое. Применяем подстановку
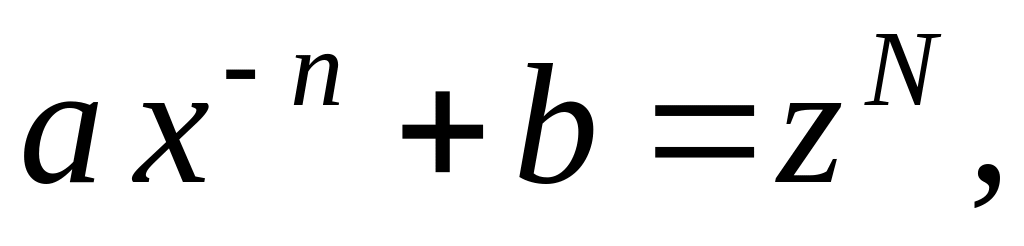 где
-
знаменатель дроби
где
-
знаменатель дроби
В
нашем случае
![]() Так как
Так как
![]() - целое, то используем подстановку для
II
случая:
- целое, то используем подстановку для
II
случая:
![]() Тогда
Тогда
![]() и
и
![]()
Исходный интеграл примет вид
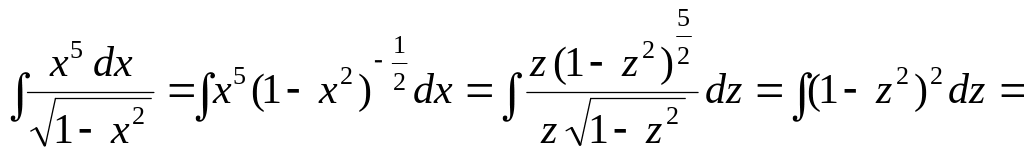
![]() где
где
![]()
Ответ:
![]() где
где
![]()
-
Задание 5
Вычислить неопределенный интеграл
5.1.

5.6.
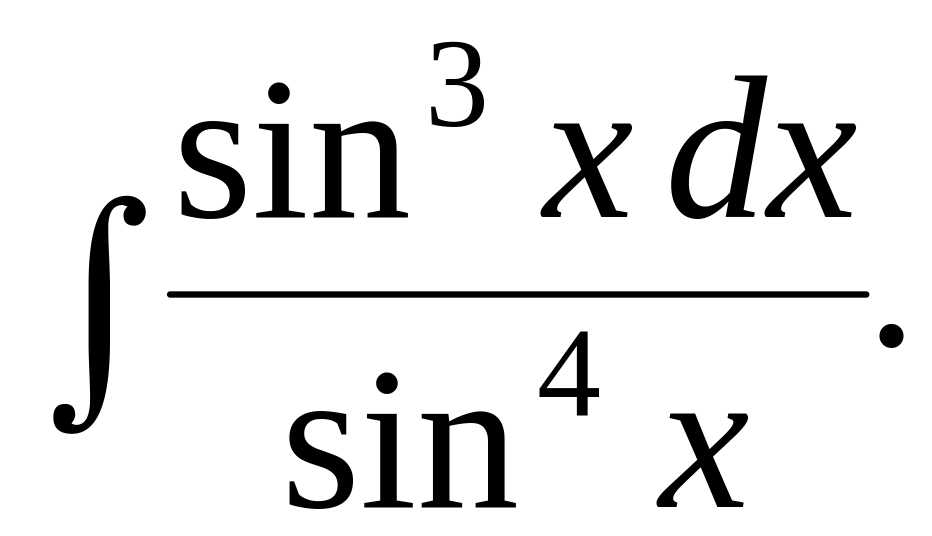
5.2.
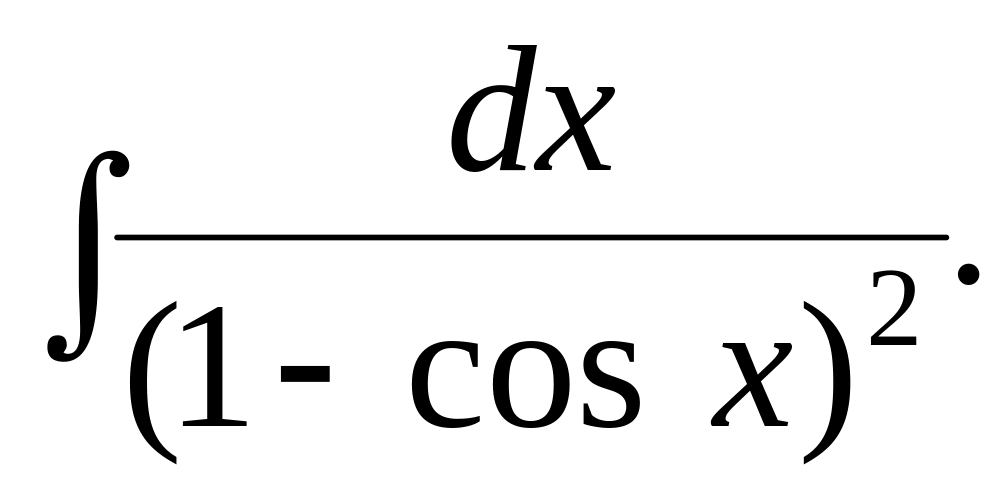
5.7.
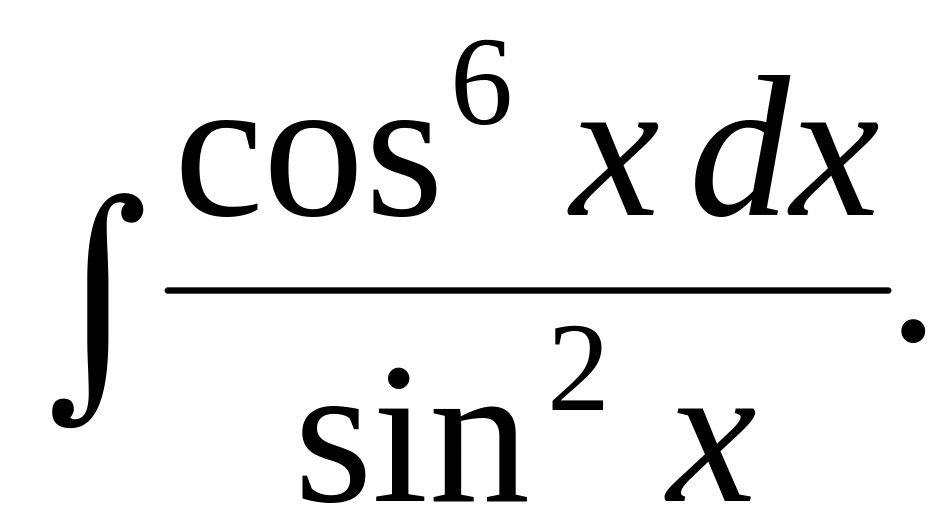
5.3.
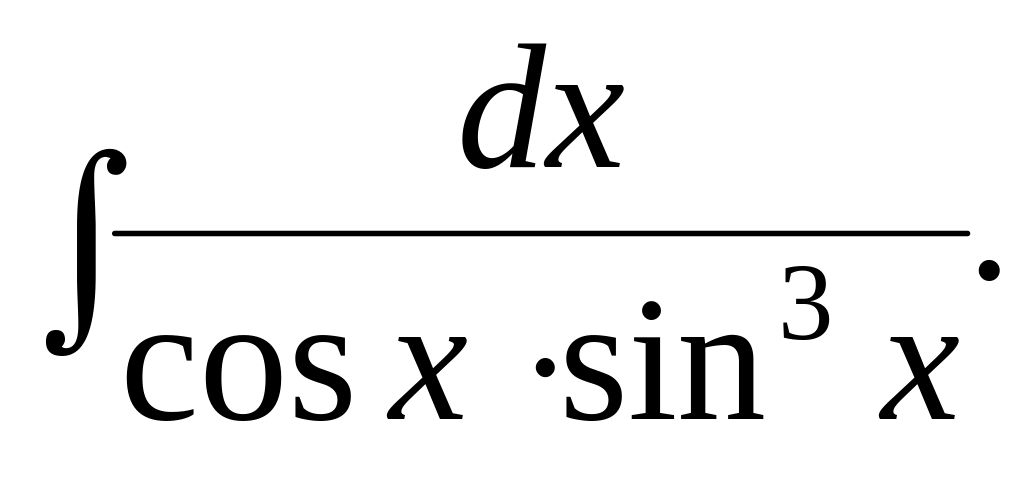
5.8.
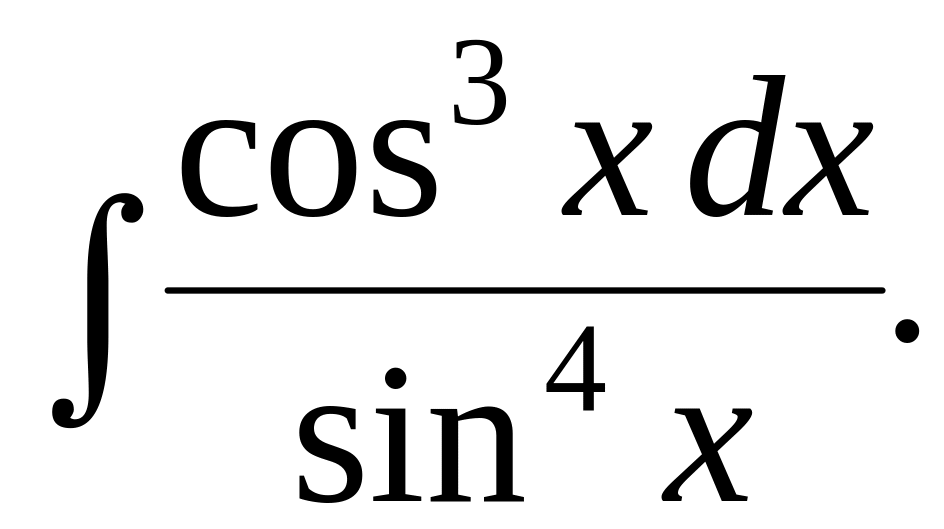
5.4.
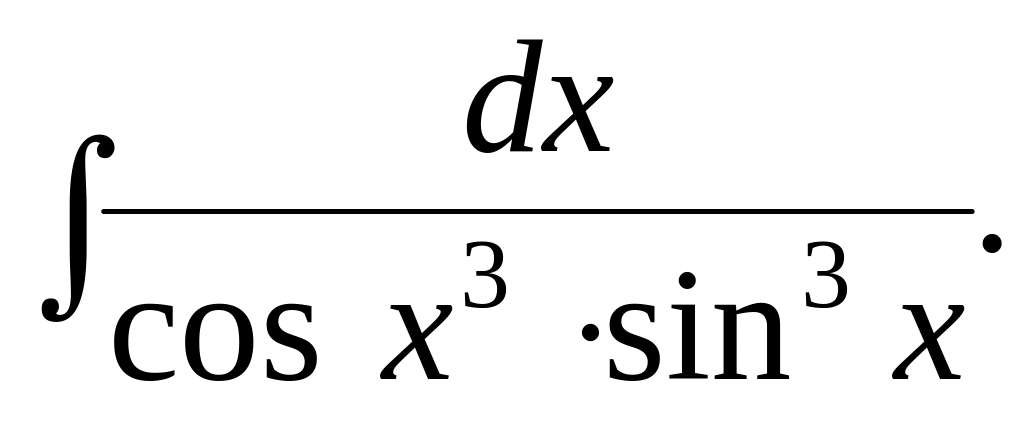
5.9.
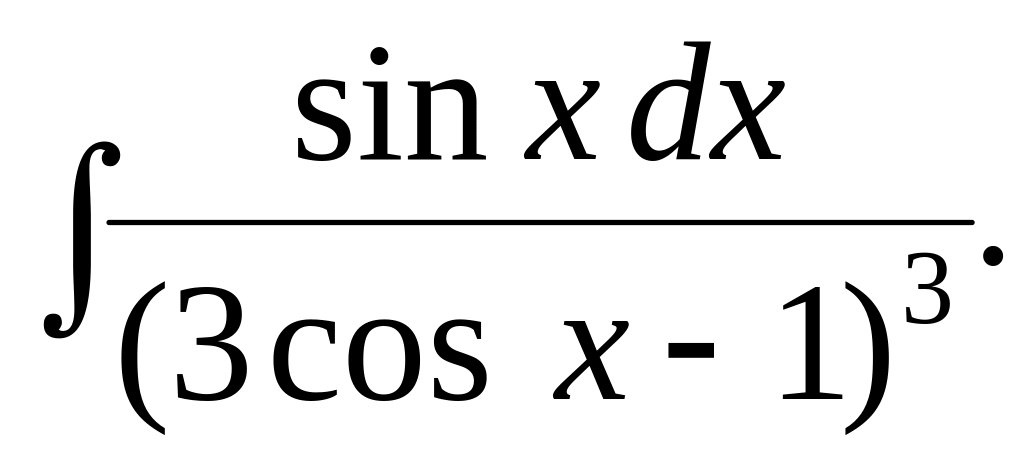
5.5.
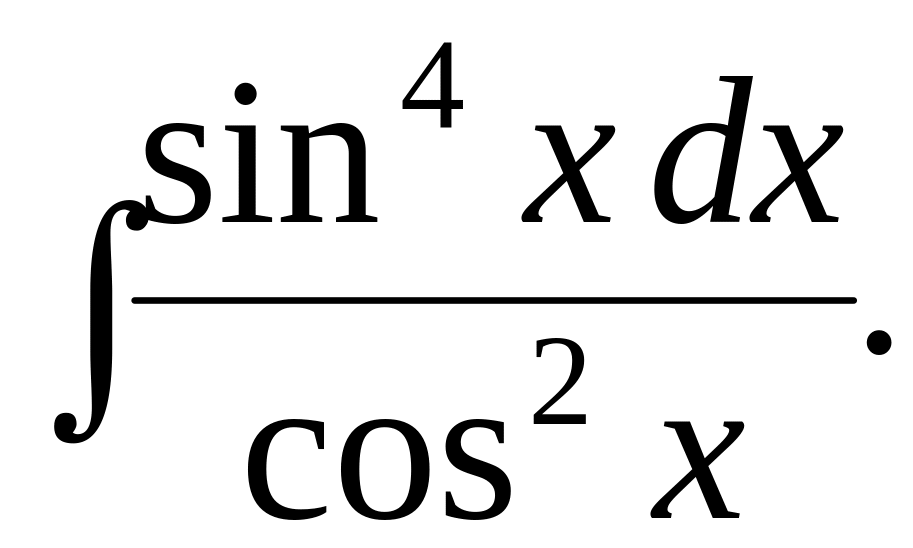
5.10.
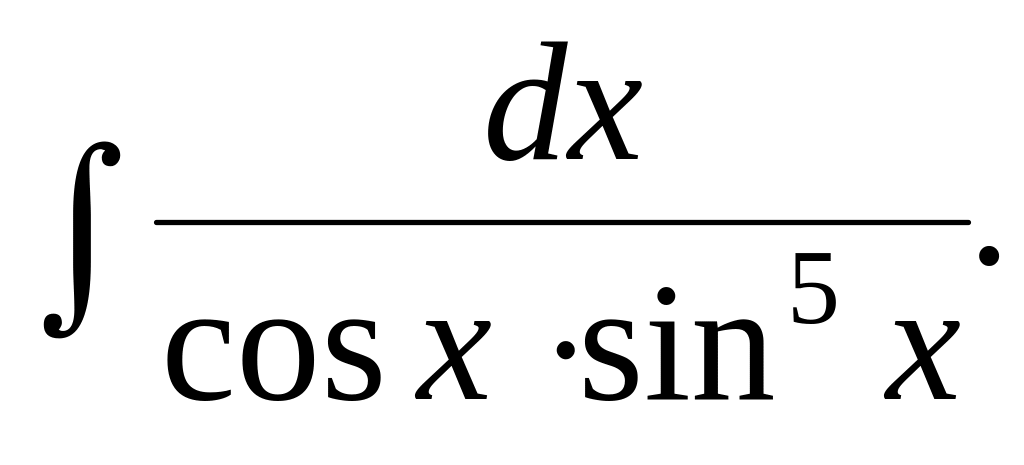
Интегралы
вида![]() ,
где в общем случае
,
где в общем случае
![]() – рациональная функция, приводятся к
интегрированию рациональных функций
с помощью универсальной подстановки
– рациональная функция, приводятся к
интегрированию рациональных функций
с помощью универсальной подстановки
![]() ,
при этом
,
при этом
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Эта подстановка ведет иногда к сложным
выкладкам. В некоторых случаях
подынтегральная функция приводится к
рациональной дроби более простым
способом:
.
Эта подстановка ведет иногда к сложным
выкладкам. В некоторых случаях
подынтегральная функция приводится к
рациональной дроби более простым
способом:
Если
 то применяется подстановка
то применяется подстановка
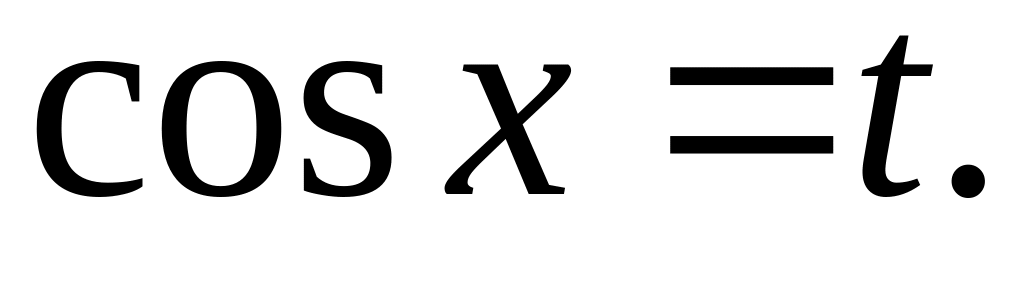
Если
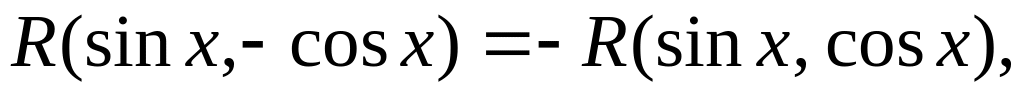 то применяется
подстановка
то применяется
подстановка

Если
 то применяется
подстановка
то применяется
подстановка
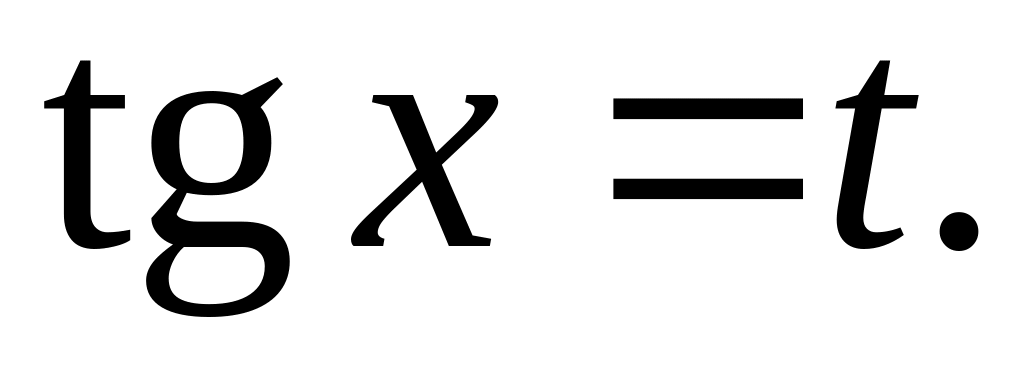
Пример
5. Найти интеграл
![]() .
.
Решение
Так как
![]() то, полагая
то, полагая
![]() ,
имеем
,
имеем

![]()
![]()
![]()
Ответ:
![]()
