
Тема: Повторение независимых испытаний Формула Бернулли
Пусть
эксперимент состоит в проведении
некоторого опыта, о котором можно
предположить, что или добились успеха
или нет. Т.е. эксперимент с двумя исходами:
А
и
![]() ,
которые называются «успехом» и «неуспехом»
соответственно.
,
которые называются «успехом» и «неуспехом»
соответственно.
Пусть
![]() ,
,
![]() .
.
Проведем п идентичных испытаний (независимых друг от друга). Построенная схема испытаний называется схемой Бернулли.
Ставится
вопрос: Какова вероятность того, что
![]() раз добьемся успеха? Обозначим искомую
вероятность
раз добьемся успеха? Обозначим искомую
вероятность
![]() .
.
Определение. Схемой Бернулли называется последовательность независимых (идентичных) испытаний с двумя исходами, имеющими неизменные вероятности (в каждом из испытаний).
Вероятность в схеме Бернулли вычисляется по формуле
![]() . (1)
. (1)
Формула (1) называется формулой Бернулли.
Отметим,
что вероятность
равна коэффициенту при
![]() в разложении бинома
в разложении бинома
![]() по степеням х.
В силу этого свойства совокупность
вероятностей
называется биномиальным законом
распределения вероятностей.
по степеням х.
В силу этого свойства совокупность
вероятностей
называется биномиальным законом
распределения вероятностей.
Пример: В помещении 6 электролампочек. Вероятность того, что каждая лампочка останется исправной в течение года, равна 0,7. Найти вероятность того, что в течение года придется заменить 2 лампочки.
Решение: А = «лампочка неисправна»
n = 6, m = 2, р =1 – 0,7 = 0,3; q = 0,7; p + q = 1,
![]() .
.
Ответ. 0,3241.
Если
требуется найти вероятность того, что
число появления события А
окажется в пределах от т1
до т2
(интервальная вероятность), обозначается
![]() или
или
![]() ,
то тогда в силу несовместимости событий
,
то тогда в силу несовместимости событий
![]() .
.
«Не
менее m
раз»
![]() .
.
«Хотя
бы 1 раз»
![]() .
.
Т.к.
все возможные несовместимые между собой
исходы испытаний состоят в появлении
события А
0 раз, 1 раз, …, n
раз, то
![]() .
.
Наивероятнейшее число появления события а в схеме Бернулли
Вероятность с увеличением m сначала возрастает, затем достигает максимума и при дальнейшем росте m убывает.
Используя
неравенства
![]() ,
,
![]() и формулу Бернулли, получаем:
и формулу Бернулли, получаем:
![]() – наивероятнейшее
число появления события А
в схеме Бернулли.
– наивероятнейшее
число появления события А
в схеме Бернулли.
Границы
отличаются на единицу, так как
![]() .
.
Пример:
Если
![]() ,
то
,
то
![]() ,
если
,
если
![]() ,
то
,
то
![]() .
.
Теоремы Пуассона и Муавра – Лапласа
При
больших значениях n
и m
вычисление
по формуле Бернулли превращается в
технически сложную задачу, следовательно,
возникла потребность в асимптотических
формулах как для
,
так и для
![]() .
.
Локальная теорема Муавра-Лапласа
При больших m и n в схеме Бернулли имеет место следующая формула
![]() ,
где
,
где
![]() .
.
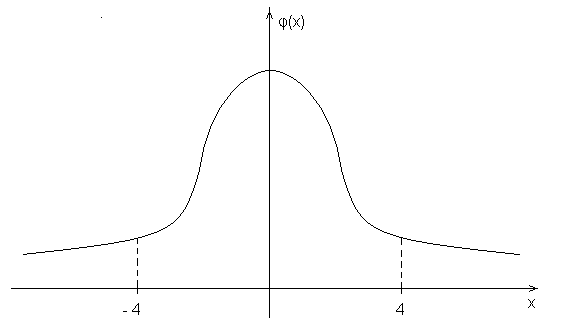
Рис.1.
График функции
![]() .
.
Для
функции
![]() есть таблицы значений для x[0;4],
есть таблицы значений для x[0;4],
![]() при
при
![]() .
Функция
четная, т. е.
.
Функция
четная, т. е.
![]() .
.
Чем больше разница между ожидаемым m и средним np, тем меньше вероятность.
Пример: Вероятность отказа каждого прибора при испытании равна 0,2. Приборы испытываются независимо друг от друга. Найти вероятность отказа 15 приборов при испытании 120 приборов.
Решение: А = «прибор отказал»
п =120; т = 15; р = 0,2; q = 1 – 0,2 = 0,8.

Ответ.
![]() 0,01.
0,01.
Интегральная теорема Муавра-Лапласа
При больших n, m1, m2 в схеме Бернулли
![]() ,
где
,
где
![]() .
.
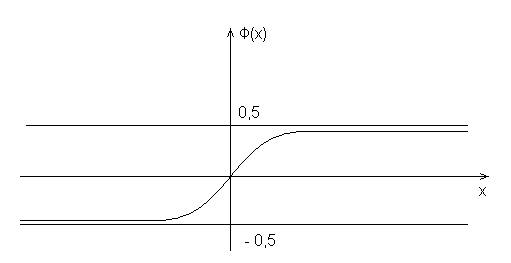
Рис.2.
График функции
![]() .
.
Функция – нормированная функция Лапласа.
![]() – нечетная,
т.е.
– нечетная,
т.е.
![]() ,
значения функции имеются в таблицах.
При
,
значения функции имеются в таблицах.
При ![]()
![]() .
.
Пример: Вероятность отказа каждого прибора при испытании равна 0,2. Приборы испытываются независимо друг от друга. Найти вероятность отказа от 10 до 25 приборов при испытании 100 приборов.
Решение: А = «прибор отказал»
п
=100;
![]() ;
;
![]() ;
р
= 0,2; q
=
1 – 0,2 = 0,8.
;
р
= 0,2; q
=
1 – 0,2 = 0,8.
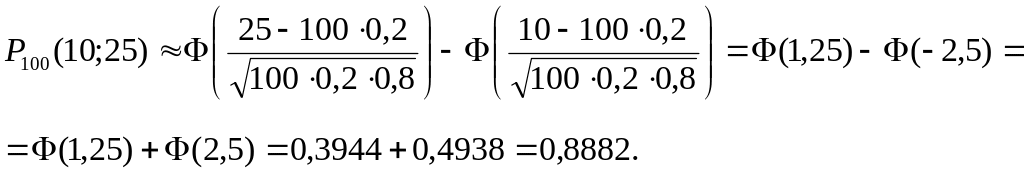
Ответ. 0,8882.
В задачах часто будет интересовать интервал, симметричный относительно np.
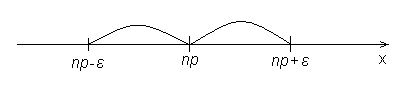
![]() .
.
Рассмотрим
частоту появления события
![]() и пусть интервал значений появления
события в схеме Бернулли симметричен
относительно np.
Тогда
и пусть интервал значений появления
события в схеме Бернулли симметричен
относительно np.
Тогда
![]() ,
где
,
где
![]() .
.
