1.3. Задачи

1. Пусть А и В- линейные операторы, действующие из Х в . Показать, что оператор С=А+В является линейным.

2. Показать, что сложение операторов обладает следующими свойствами:

А+В=В+А,

(А+В)+С=А+(В+С).

3. Пусть А и В- линейные операторы. Показать, что оператор С=АВ является линейным.

4. Выяснить, какие из следующих операторов А, определенных путем задания координат вектора как функций координат вектора , являются линейными, и найти их матрицы в том же базисе, в котором заданы координаты вектора :

а)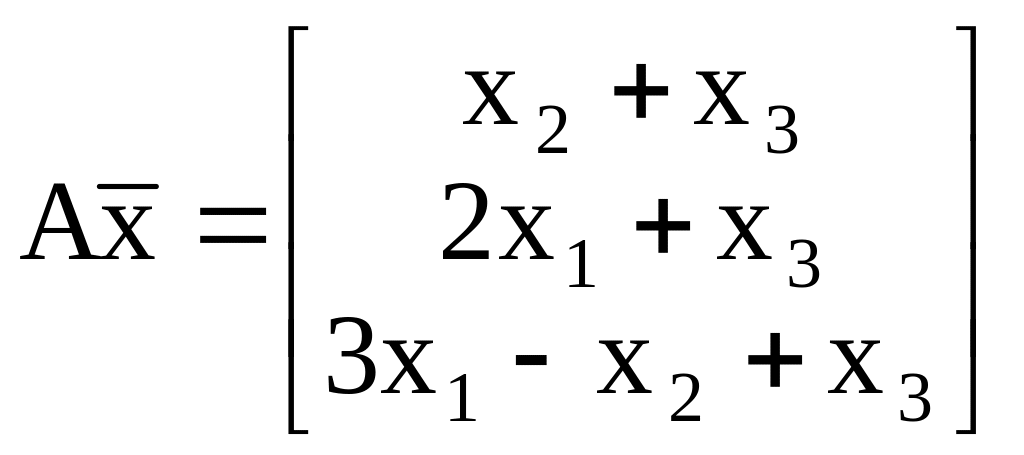 b) с)

5. Доказать, что существует единственное линейное преобразование трехмерного пространства, переводящее векторы соответственно в и найти матрицу этого преобразования в том же базисе, в котором заданы координаты всех векторов:

6. Линейное преобразование  в базисе , , имеет матрицу

Найти его матрицу в базисе , , .

7. Пусть оператор А в базисе имеет матрицу , оператор В в базисе имеет матрицу . Найти матрицу оператора А+В в базисе .

8. Доказать, что любое линейное преобразование А одномерного пространства сводится к умножению всех векторов на одно и то же число, т.е. .

9. Как изменится матрица линейного оператора, если в базисе поменять местами векторы и ?

2. Образ и ядро линейного оператора

Определение 1. Образом линейного оператора А называется множество всех элементов , представимых в виде , где .

Образ линейного оператора А является линейным подпространством пространства . Его размерность называется рангом оператора А.

Определение 2. Ядром линейного оператора А называется множество всех векторов , для которых .

Ядро является линейным подпространством пространства Х. Его размерность называется дефектом оператора А.

Если оператор А действует в ¤ -мерном пространстве Х, то справедливо следующее соотношение + = .

Оператор А называется невырожденным, если его ядро . Ранг невырожденного оператора равен размерности пространства Х.

Пусть - матрица линейного преобразования А пространства Х в некотором базисе, тогда координаты образа и прообраза связаны соотношением

.

Поэтому координаты любого вектора удовлетворяют системе уравнений

.

Отсюда следует, что ядро линейного оператора является линейной оболочкой фундаментальной системы решений данной системы.

2.1. Задачи

1. Доказать, что ранг оператора равен рангу его матрицы в произвольном базисе.

Вычислить ядра линейных операторов, заданных в некотором базисе пространства Х следующими матрицами:

2. 3.

4.

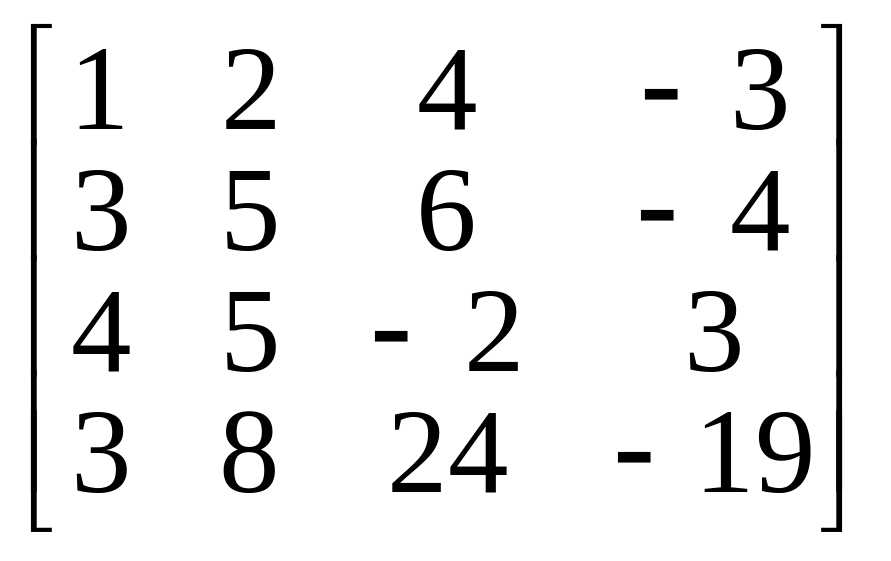
5. Доказать, что .

Вычислить ранг и дефект операторов, заданных следующими матрицами:

6. . 7. . 8. .

2. Собственные векторы и собственные значения линейного оператора

Рассмотрим линейный оператор А, действующий в - мерном пространстве Х.

Определение. Число  называется собственным значением оператора А, если , такой, что . При этом вектор называется собственным вектором оператора А.

Важнейшим свойством собственных векторов линейного оператора является то, что собственные векторы, соответствующие попарно различным собственным значениям линейно независимы.

Если - матрица линейного оператора А в базисе пространства Х, то собственные значения  и собственные векторы оператора А определяются следующим образом:

1. Собственные значения находят как корни характеристического уравнения (алгебраического уравнения -ой степени):

.

2. Координаты всех линейно независимых собственных векторов , соответствующих каждому отдельному собственному значению , получают, решая систему однородных линейных уравнений:

матрица которой имеет ранг . Фундаментальные решения этой системы являются вектор – столбцами из координат собственных векторов.

Корни характеристического уравнения называют также собственными значениями матрицы , а решения системы - собственными векторами матрицы .

Пример. Найти собственные векторы и собственные значения оператора А, заданного в некотором базисе матрицей

1. Для определения собственных значений составляем и решаем характеристическое уравнение :

.

Отсюда собственное значение , его кратность .

2. Для определения собственных векторов составляем и решаем систему уравнений :

Эквивалентная система базисных уравнений имеет вид

Поэтому всякий собственный вектор представляет собой вектор-столбец , где с – произвольная константа.