
- •Непосредственное интегрирование
- •Примеры решения задач
- •Метод замены переменной и формула интегрирования по частям
- •Примеры решения задач
- •Интегрирование рациональных дробей
- •Примеры решения задач
- •Интегрирование тригонометрических функций
- •Примеры решения задач
- •Интегрирование иррациональных функций
- •Примеры решения задач
- •Определённый интеграл
- •Примеры решения задач
- •Несобственные интегралы
- •Примеры решения задач
- •Приложения определённого интеграла
- •Примеры решения задач
- •Частные производные первого и высшего порядков. Дифференциал функции нескольких переменных.
- •Примеры решения задач
- •Производная сложной и неявно заданной функции нескольких переменных. Касательная плоскость и нормаль к поверхности
- •Примеры решения задач
- •Экстремум функции двух переменных
- •Примеры решения задач
- •Дифференциальные уравнения с разделяющимися переменными, однородные и сводящиеся к однородным уравнения
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Линейные уравнения первого порядка, уравнение Бернулли. Уравнение в полных дифференциалах
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Дифференциальные уравнения высших порядков. Уравнения, допускающие понижения порядка
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Линейные однородные и неоднородные уравнения с постоянными коэффициентами, метод вариации постоянной
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Линейные неоднородные уравнения с постоянными коэффициентами с правой частью специального вида
- •Примеры решения задач
- •Задачи для самостоятельного решения
Несобственные интегралы
Несобственными называются интегралы с бесконечными пределами (несобственные интегралы 1-го рода) и интегралы от неограниченных функций (несобственные интегралы 2-го рода).
Несобственные интегралы 1-го рода определяются следующим образом:
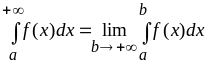 ;
;
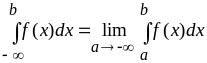 ;
;
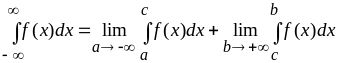 ,
,
где
![]() – произвольное число.
– произвольное число.
Эти интегралы называются сходящимися, если существуют конечные пределы в правых частях равенств. Если же указанные пределы не существуют или бесконечны, то соответствующие интегралы называются расходящимися.
Несобственные интегралы 2-го рода определяются следующим образом:
 ,
если функция
,
если функция
![]() имеет бесконечный разрыв при
имеет бесконечный разрыв при
![]() ;
;
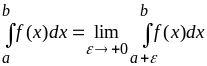 ,
если функция
имеет бесконечный разрыв при
,
если функция
имеет бесконечный разрыв при
![]() ;
;
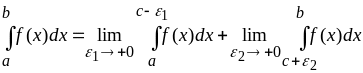 ,
если функция
имеет бесконечный разрыв в точке
,
если функция
имеет бесконечный разрыв в точке
![]() ,
,
![]() .
.
Критерии
сходимости
формулируются для интегралов вида
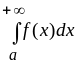 ;
для других несобственных интегралов
справедливы аналогичные утверждения.
;
для других несобственных интегралов
справедливы аналогичные утверждения.
1.
Если на промежутке
![]() функции
и
функции
и
![]() удовлетворяют условию
удовлетворяют условию
![]() ,
то из сходимости интеграла
,
то из сходимости интеграла
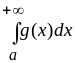 следует сходимость интеграла
,
а из расходимости
– расходимость
.
следует сходимость интеграла
,
а из расходимости
– расходимость
.
2.
Если функции
и
неотрицательны и существует предел
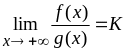 ,
,
![]() ,
то интегралы
и
одновременно оба сходятся или оба
расходятся.
,
то интегралы
и
одновременно оба сходятся или оба
расходятся.
В
качестве функции
сравнения
в случае
особенно удобно использовать функцию
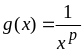 (
(![]() ),
а в случае интеграла
),
а в случае интеграла
 от неограниченной в окрестности точки
функции – функцию
от неограниченной в окрестности точки
функции – функцию
 .
Можно показать (см. лекции!), что интеграл
.
Можно показать (см. лекции!), что интеграл
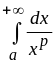 сходится при
сходится при
![]() и расходится при
и расходится при
![]() ,
а интеграл
,
а интеграл
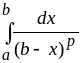 (как и интеграл
(как и интеграл
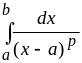 )
сходится при
)
сходится при
![]() и расходится при
и расходится при
![]() .
.
Примеры решения задач
Вычислить несобственные интегралы или установить их расходимость: а)
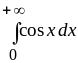 ;
б)
;
б)
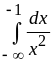 ;
в)
;
в)
 .
.
Решение.
а)
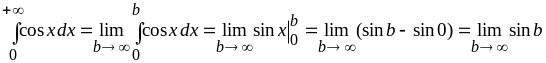
Такой предел не существует. Следовательно, несобственный интеграл расходится.
б)
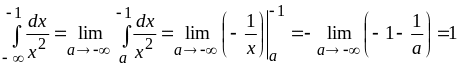 ,
,
т. е. несобственный интеграл сходится и его значение равно 1.
в) Подынтегральная функция – чётная, поэтому
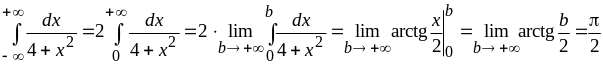
то
есть интеграл сходится и его значение
равно
![]() .
.
2.
Исследовать на сходимость интегралы:
а)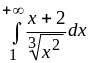 ;
б)
;
б)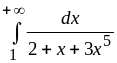 .
.
Решение.
а)
Здесь
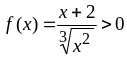 при
при
![]() ,
при этом
,
при этом
 .
Но интеграл
.
Но интеграл
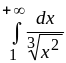 расходится (
расходится (![]() ).
Поэтому, согласно признаку сравнения
1, интеграл
расходится.
).
Поэтому, согласно признаку сравнения
1, интеграл
расходится.
б)
Здесь
 при
.
Рассмотрим функцию
при
.
Рассмотрим функцию
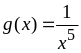 ,
интеграл от которой
,
интеграл от которой
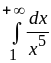 сходится (
сходится (![]() ).
А так как существует предел
).
А так как существует предел
 ,
то интеграл
также сходится (признак сравнения 2).
,
то интеграл
также сходится (признак сравнения 2).
3.
Вычислить несобственные интегралы или
установить их расходимость: а)
![]() ;
б)
;
б)
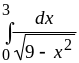 ;
в)
;
в)
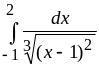 .
.
Решение.
а)
Подынтегральная функция
![]() в точке
неограниченна, поэтому
в точке
неограниченна, поэтому
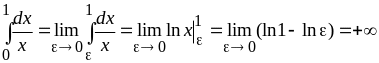 ,
,
т. е. несобственный интеграл расходится.
б) Подынтегральная функция терпит разрыв при . Поэтому
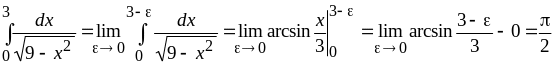 ,
,
т. е. интеграл сходится и его значение равно .
в) Подынтегральная функция терпит разрыв при . Поэтому
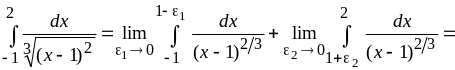
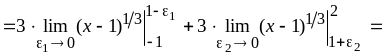
![]() ,
,
т. е. интеграл сходится.
4.
Исследовать на сходимость интегралы:
а) ;
б)
;
б)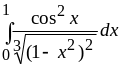 .
.
Решение.
а)
Подынтегральная функция
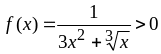 при
при
![]() и неограниченна в точке
,
при этом
и неограниченна в точке
,
при этом
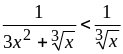 .
Но интеграл
.
Но интеграл
![]() сходится (
сходится (![]() ).
Поэтому, согласно признаку сравнения
1, интеграл
также сходится.
).
Поэтому, согласно признаку сравнения
1, интеграл
также сходится.
б)
Функция
 терпит бесконечный разрыв в точке
.
Перепишем её в виде
терпит бесконечный разрыв в точке
.
Перепишем её в виде
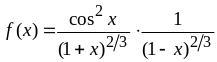 и сравним с функцией
и сравним с функцией
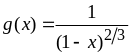 .
Интеграл
.
Интеграл
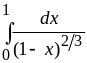 сходится (
).
Так как
сходится (
).
Так как
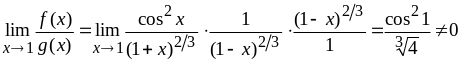 ,
,
то, согласно предельному признаку сравнения 2, интеграл также сходится.
Задачи для самостоятельного решения
Вычислить несобственные интегралы или установить их расходимость:
1.
 Ответ:
Ответ:
![]() .
.
2.
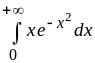 Ответ:
Ответ:
![]() .
.
3.
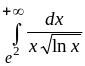 Ответ:
расходится.
Ответ:
расходится.
4.
 Ответ:
расходится.
Ответ:
расходится.
5.
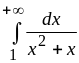 Ответ:
Ответ:
![]() .
.
6.
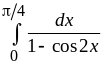 Ответ:
расходится.
Ответ:
расходится.
7.
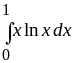 Ответ:
Ответ:
![]() .
.
8.
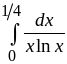 Ответ:
расходится.
Ответ:
расходится.
9.
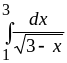 Ответ:
Ответ:
![]() .
.
10.
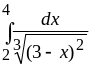 Ответ:
Ответ:
![]() .
.
Исследовать на сходимость интегралы:
1.
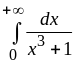 Ответ:
Ответ:
![]() .
.
2.
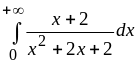 Ответ:
расходится.
Ответ:
расходится.
3.
 Ответ:
Ответ:
![]() .
.
4.
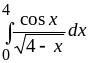 Ответ:
сходится.
Ответ:
сходится.
5.
 Ответ:
сходится.
Ответ:
сходится.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 8
