ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 1.
Непосредственное интегрирование
Функция
называется первообразной
для функции
,
если
или
.
Если функция
имеет первообразную
,
то она имеет бесконечное множество
первообразных, причём все первообразные
содержатся в выражении
,
где
– постоянная. Неопределённым
интегралом
от функции
называется совокупность всех её
первообразных. Обозначение:
.
Свойства неопределённого интеграла (правила интегрирования):
1°.
или
.
2°.
.
3°.
,
где
– постоянная.
4°.
.
5°.
Если
и
,
то
(инвариантность формулы интегрирования).
Таблица основных интегралов:
1.
(
)
.
2.
.
3.
4.
5.
6.
|
7.
8.
9
.
10.
|
.
.
.
.
.
.
.
.
11
.
12.
.
13.
.
14.
.
15.
.
16.
.
17.
.
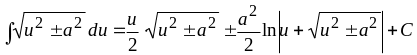Отметим,
что в приведённой таблице переменная
может обозначать как независимую
переменную, так и функцию от независимой
переменной (согласно свойству 5°).
При
сведении данного интеграла к табличному
часто используется приём подведения
функции под знак дифференциала по
формуле
,
например,
(здесь
– число),
(
),
,
,
и т. д. с тем, чтобы далее, в соответствии
со свойством 5°, воспользоваться
табличными интегралами.
Примеры решения задач
1.
Используя таблицу, найти следующие
интегралы: а)
;
б)
;
в)
;
г)
.
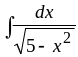Решение.
а)
Воспользуемся табличным интегралом 1
(
):
.
б) Аналогично находим:
.
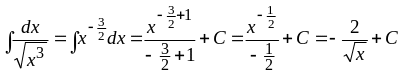в)
Используя табличный интеграл 11 (
),
находим:
.
г)
Подставляя
в табличный интеграл 14, получим:
.
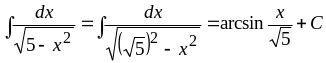2.
Используя таблицу и основные свойства
неопределённого интеграла, найти
интеграл: а)
;
б)
;
в)
;
г)
.
Решение.
а) Воспользуемся свойствами 3° и 4° неопределённого интеграла, а затем табличными интегралами 11, 2, 1:
.
б)
Почленно поделим числитель подынтегральной
дроби на знаменатель:
.
Отсюда
в) Преобразуем подынтегральную дробь:
.
Тогда с учётом табличных интегралов 1 и 12, имеем
.
г) Используем известные формулы тригонометрии, а также табличные интегралы 6 и 1:
.
3.
С помощью приёма подведения функции
под знак дифференциала найти интегралы:
а)
;
б)
;
в)
;
г)
.
Решение.
а)
Этот интеграл можно привести к табличной
формуле 2 (
):
.
б)
Здесь относительно переменной
получаем интеграл от степенной функции:
.
в)
Поскольку
,
то имеем:
.
г)
Так как
,
то
.
Задачи для самостоятельного решения
1.
Ответ:
.
2.
Ответ:
.
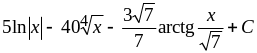3.
Ответ:
.
4.
Ответ:
.
5.
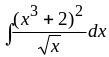Ответ:
.
6.
Ответ:
7.
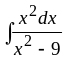Ответ:
.
8.
Ответ:
.
9.
Ответ:
.
10.
Ответ:
.
11.
Ответ:
.
12.
Ответ:
.
13.
Ответ:
.
14.
Ответ:
.
15.
Ответ:
.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 2
Метод замены переменной и формула интегрирования по частям
Замена переменной в неопределённом интеграле производится с помощью подстановок двух видов:
1)
,
где
– монотонная, непрерывно дифференцируемая
функция новой переменной
.
Формула замены переменной в этом случае
имеет вид:
;
2)
,
где
– новая переменная. Формула замены
переменной при такой подстановке:
.
Получающиеся после применения подстановки интегралы должны быть более удобны для интегрирования, чем исходные.
Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.
Интегрированием по частям называется нахождение интеграла по формуле
,
где
,
– непрерывно дифференцируемые функции
от
.
С помощью этой формулы нахождение
интеграла
сводится к отысканию другого интеграла
;
её применение целесообразно в тех
случаях, когда последний интеграл либо
проще исходного, либо ему подобен. При
этом за
берётся такая функция, которая при
дифференцировании упрощается, а за
– та часть подынтегрального выражения,
интеграл от которой известен или может
быть найден.
Укажем некоторые типы интегралов, которые удобно вычислять методом интегрирования по частям.
1.
Интегралы вида
,
,
,
где
– многочлен,
– число. Удобно положить
,
а за
принять все остальные сомножители.
2.
Интегралы вида
,
,
,
,
.
Удобно положить
,
а за
принять остальные сомножители.
3.
Интегралы вида
,
,
где
и
– числа. За
можно принять функцию
.