
- •4. Законы сохранения
- •4.1.Сохраняющиеся величины
- •4.2.Кинетическая энергия. Работа. Мощность.
- •4.3. Несколько примеров на вычисление работы.
- •Работа упругой силы
- •2) Работа гравитационной (или кулоновской) силы
- •Работа однородной силы тяжести.
- •4.3.Потенциальное поле сил. Консервативные силы.
- •4.4. Потенциальная энергия во внешнем поле сил.
- •4.5. Потенциальная энергия взаимодействия.
- •4.6. Закон сохранения энергии
- •4.7.Закон сохранения импульса
- •4.8. Соударение двух тел.
- •4.9. Закон сохранения момента импульса.
4.3. Несколько примеров на вычисление работы.
Работа упругой силы
 Работа
упругой силы
Работа
упругой силы
![]() ,
,
 где
где
![]() — радиус-вектор
частицы М
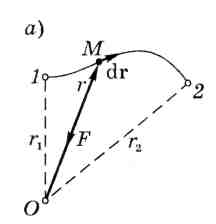
относительно точки О (рис. 4.3, а).
— радиус-вектор
частицы М
относительно точки О (рис. 4.3, а).
Переместим частицу М, на которую действует эта сила, по произвольному пути из точки 1 в точку 2.
Найдем сначала элементарную работу силы F на элементарном перемещении dr:
![]()
Скалярное
произведение
![]() где (
где (![]() )r
— проекция
на вектор
.
)r
— проекция
на вектор
.
Эта проекция равна
dr
— приращению модуля вектора
. Поэтому и
![]()
![]()
Теперь вычислим работу данной силы на всем пути, т. е. проинтегрируем последнее выражение от точки 1 до точки 2:
![]()
2) Работа гравитационной (или кулоновской) силы
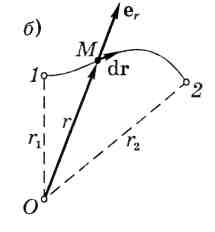
Пусть в точке О (рис. 4.3, б) находится неподвижный силовой центр — материальная точка, действующая на частицу М с силой F, которая как для гравитационного, так и для кулоновского взаимодействий может быть представлена в виде
![]()
где
![]() —
соответствующая
постоянная
—
соответствующая
постоянная![]() или
или
![]() ,
,
r — расстояние от точки О до частицы М,
еr — орт радиуса-вектора .
Элементарная работа этой силы на перемещение
![]()
Скалярное произведение
где ( )r — проекция на вектор . Эта проекция равна dr — приращению модуля вектора . Поэтому и
поэтому
![]()
Работа этой силы
на всем пути от точки 1 до точки 2
![]()
Работа однородной силы тяжести.
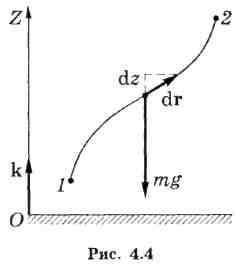
Запишем эту силу
в виде![]() ,
где
,
где
![]() —
орт вертикальной
оси Z,
положительное направление которой
выбрано вверх (рис. 4.4).
—
орт вертикальной
оси Z,
положительное направление которой
выбрано вверх (рис. 4.4).
Элементарная работа силы тяжести на перемещении :
![]()
Скалярное
произведение![]() ,
где
,
где![]() —
проекция на
орт
, равная dz — приращению координаты z.
Поэтому
—
проекция на
орт
, равная dz — приращению координаты z.
Поэтому
![]() и
и
![]()
Работа данной силы на всем пути от точки 1 до точки
![]() (4.5)
(4.5)
Рассмотренные силы интересны тем, что их работа, как видно из (4.3)-(4.5),
не зависит от формы пути между точками 1 и 2,
зависит только от положения этих точек.
Эта весьма важная особенность данных сил присуща, однако, не всем силам.
Например, сила трения этим свойством не обладает: работа этой силы зависит не только от положения начальной и конечной точек, но и от формы пути между ними.
4.3.Потенциальное поле сил. Консервативные силы.
Если частица в каждой точке пространства подвержена воздействию других тел, то говорят, что эта частица находится в поле сил.
Например,
вблизи поверхности Земли частица находится в поле силы тяжести.
В
 электрическом поле неподвижного
точечного заряда
электрическом поле неподвижного
точечного заряда
 на заряженную частицу действует поле,
характерное тем, что направление силы,
действующей на частицу в любой точке
пространства, проходит через неподвижный
центр (заряд
),
а величина силы зависит только от
расстояния до этого центра:
на заряженную частицу действует поле,
характерное тем, что направление силы,
действующей на частицу в любой точке
пространства, проходит через неподвижный
центр (заряд
),
а величина силы зависит только от
расстояния до этого центра:
 .
Такое поле
называется центральным
(рис.4.3).
.
Такое поле
называется центральным
(рис.4.3).
Если в каждой точке поля сила, действующая на частицу, одинакова по величине и направлению, поле называется однородным.
Силовое поле, которое можно описать с помощью функции такой, что
![]() (4.6)
(4.6)
называется потенциальным.
Функция называется потенциальной функцией или потенциалом.
Если поле не
изменяется со временем, оно называется
стационарным,
в этом случае
![]() .
.
Добавление к
функции
произвольной постоянной величины не
изменяет значений
![]() ,
вычисляемых по формулам (4.6) . Поэтому
потенциальная функция определяется с
точностью до произвольной аддитивной
постоянной. Однако при фиксированном
значении этой постоянной
становится однозначной функцией
координат и времени.
,
вычисляемых по формулам (4.6) . Поэтому
потенциальная функция определяется с
точностью до произвольной аддитивной
постоянной. Однако при фиксированном
значении этой постоянной
становится однозначной функцией
координат и времени.
Вектор с
компонентами
![]() ,
где
,
где
![]() -
скалярная функция координат, называется
градиентом
функции
и обозначается
-
скалярная функция координат, называется
градиентом
функции
и обозначается
![]() либо
либо
![]()
(![]() называется
оператором набла,
читается:
«набла фи» или «градиент фи»).
называется
оператором набла,
читается:
«набла фи» или «градиент фи»).
Из определения
градиента следует, что
![]() ,
,
поэтому в случае потенциального силового поля имеем:
![]() .
(4.7)
.
(4.7)
Работа силы, удовлетворяющей условию (4.7), равна
![]()
![]() ,
(4.8)
,
(4.8)
т.е. представляет
собой полный дифференциал функции
![]() .
.
Проинтегрировав выражение (4.8) по некоторой траектории от точки 1 до точки 2, получаем:
![]() .
(4.9)
.
(4.9)
Форма траектории, по которой осуществлялось интегрирование, была совершенно произвольной.
Таким образом, работа, совершаемая над частицей силами стационарного потенциального поля,
не зависит от пути, по которому двигалась частица,
определяется только начальным и конечным положениями частицы в пространстве.
работа таких сил на замкнутом пути равна нулю.
Силы, работа которых не зависит от пути, по которому частица переходит из одного положения в другое, называются консервативными. Следовательно, силы, действующие на частицу в стационарном потенциальном поле, являются консервативными.
Из независимости работы консервативных сил от пути вытекает, что работа таких сил на замкнутом пути равна нулю.
Ч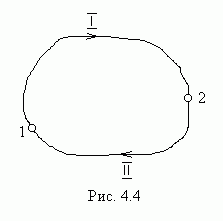 тобы
доказать это,
тобы
доказать это,
разобьем произвольный замкнутый путь (рис.4.4) на две части:
- путь 1, по которому частица переходит из точки 1 в точку 2,
- и
путь
![]() ,
по которому частица переходит из точки
2 в точку 1. При этом точки 1 и 2 выбраны
произвольно.
,
по которому частица переходит из точки
2 в точку 1. При этом точки 1 и 2 выбраны
произвольно.
Работа на всем замкнутом пути равна сумме работ, совершаемых на каждом из участков:
![]() .
(4.10)
.
(4.10)
Очевидно, работы
![]() и
и
![]() отличаются
только знаком. Действительно, изменение
направления движения на обратное
приводит к замене
на
-
,
поэтому значение интеграла
отличаются
только знаком. Действительно, изменение
направления движения на обратное
приводит к замене
на
-
,
поэтому значение интеграла
![]() изменяет знак на обратный.
изменяет знак на обратный.
Поэтому равенство
(4.10) можно записать в виде:
![]() .
.
Так как работа не
зависит от пути, то
=
-
,
и
![]() .
.
Кроме консервативных сил существуют неконсервативные силы. К ним относятся диссипативные силы, переводящие механическую энергию во внутреннюю.
Это силы
трения, сопротивления среды,
гироскопические силы, перпендикулярные скорости (сила Кориолиса, сила Лоренца), работа которых всегда равна нулю.
Для неконсервативных сил соотношение (4.7) не выполняется.
Д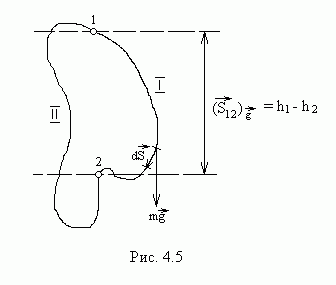 окажем,
что сила тяжести является консервативной.
окажем,
что сила тяжести является консервативной.
Эта сила в любой точке имеет одинаковые величину и направление – вниз по вертикали (рис.4.5).
Поэтому, независимо от того, по какому из путей 1 или II движется частица, работа определяется выражением:
![]()
Из рис.4.5 видно,
что проекция вектора
на направление
![]() равна разности высот
равна разности высот
![]() .
.
Тогда работа
![]()
Это выражение не зависит от пути, следовательно, сила тяжести консервативна.
Силы, действующие на частицу в центральном поле, также консервативны (рис.4.6).
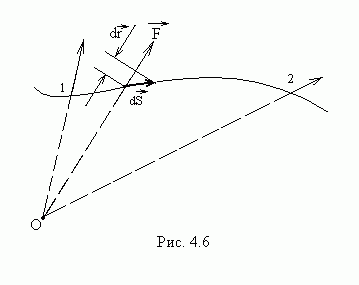 Элементарная
работа центральной силы на пути
равна
Элементарная
работа центральной силы на пути
равна
![]() .
.
Проекция
на направление силы в данном месте –
это проекция на направление радиуса-вектора
, она равна приращению расстояния частицы
до центра силового поля О:
![]() .
.
Работа на всем
пути
![]()
Это выражение
зависит только от вида функции
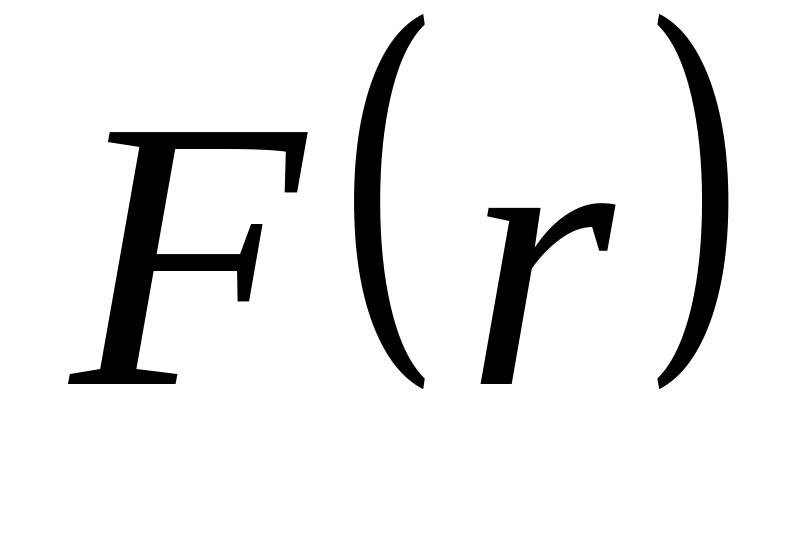 и от значений
и от значений
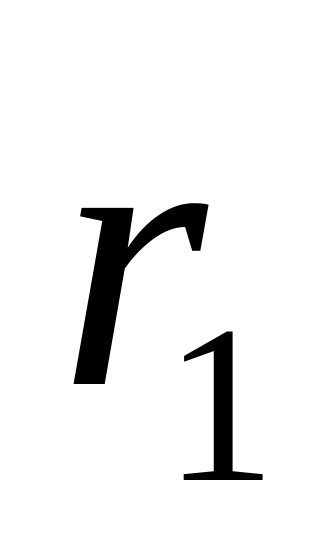 и
и
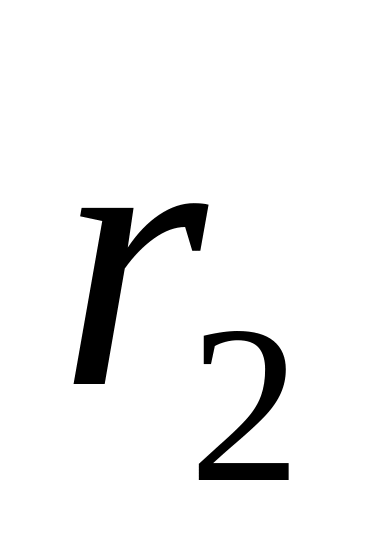 .
.
не зависит от вида траектории.
Следовательно, центральная сила консервативна.
