Геометрическое определение вероятности

Геометрическое определение вероятности является обобщением классического определения вероятности на случай, когда множество равновозможных исходов бесконечно.

Говорят, что случайный эксперимент удовлетворяет геометрическому определению вероятности, если:

• исходы эксперимента можно изобразить точками некоторой области , имеющей конечную меру ;

• можно считать, что попадание точки в любые области , имеющие одинаковую конечную меру , равновозможно и не зависит от формы и расположения внутри . При этом говорят, что точка равномерно распределена в области или бросается в область наудачу.

Согласно геометрическому определению вероятности вероятность попадания точки в любую область (событие ) пропорциональна ее мере и равна:

.

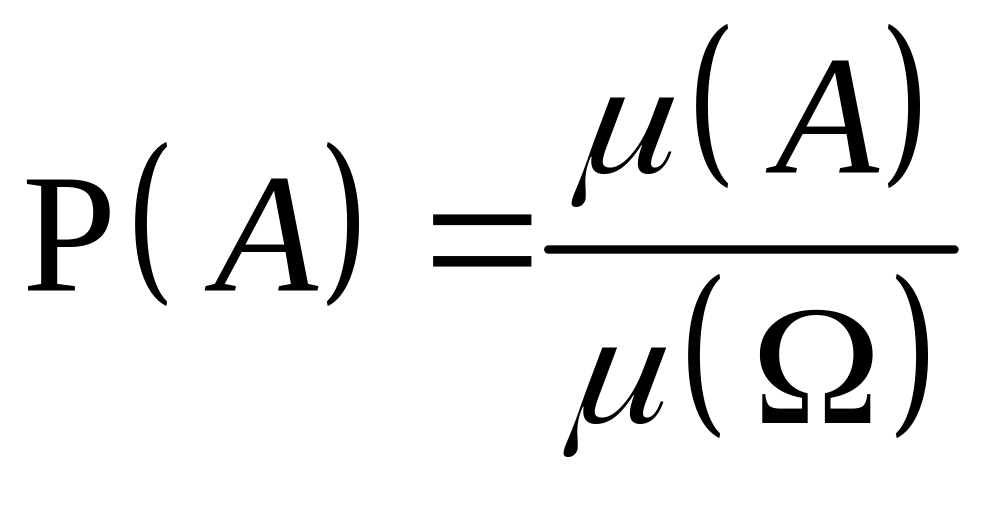В частности:

при под мерой понимается длина подмножества на прямой и

;

п

A

ри под мерой понимается площадь подмножества на плоскости и



;

п ри под мерой понимается объем подмножества на пространстве и

.

Из геометрического определения вероятности вытекают следующие свойства вероятности.

Следовательно, справедливы и свойства вероятности 4° – 7°, доказательство которых в классическом определении вероятности, основывалось только на свойствах 1° – 3°.

П

t₂

ример.

На обслуживающее устройство в промежутке времени равновозможно поступление двух заявок. Время обслуживания одной заявки равно . Если очередная заявка поступает в момент занятости устройства обслуживанием предыдущей, то она теряется. Найти вероятность потери заявки.

Решение. Обозначим t1, t2  моменты поступления заявок. Тогда Интересующее нас событие А имеет вид: . Поэтому (см. рисунок) .

T  t1 T 

Статистическое определение вероятности

Существует большой класс событий, к которым предыдущие определения вероятности не применимы из-за отсутствия равновозможности исходов. Статистическое определение вероятности позволяет приближенно находить вероятности любых случайных событий.

Для статистически устойчивого события А частота его появления в n случайных экспериментах при больших n сохраняет почти постоянную величину. Причём, для тех случаев, к которым применимы классическое и геометрическое определения вероятности, можно показать, что эта постоянная величина есть не что иное, как вероятность события А. Естественно предположить, что и в случаях, не сводящихся к классической и геометрической схемам, постоянная, около которой происходит колебание частоты события А, есть его вероятность . Многочисленные эксперименты подтверждают это.

Согласно статистическому определению вероятности за вероятность события А принимается частота при достаточно большом n:

.

Частота обладает всеми свойствами вероятности из предыдущих двух определений:

1. ;

2. ;

3. .

Однако, частота не совпадает с истинной вероятностью даже при очень больших n. Более того, если провести другую серию из n экспериментов, то значение частоты будет, вообще говоря, другим. Это означает, что колебание частоты около вероятности носит случайный характер. Поэтому приближенное равенство следует понимать, как приближённое равенство чисел, имеющее большую степень достоверности, но не абсолютно достоверное. Аналогично, и сходимость частоты к при n  , следует понимать не в смысле сходимости числовой последовательности, а в некотором специфическом смысле, учитывающем случайность (в теории вероятностей эта сходимость называется сходимостью по вероятности и мы с ней будем неоднократно иметь дело в дальнейшем).

Статистическое определение вероятности является универсальным, поскольку применимо к любым случайным экспериментам и связанным с ними случайным событиям. Недостаток этого определения состоит в том, что оно требует проведения большого числа экспериментов для получения результата.