ФЕДЕРАЛЬНОЕ АГЕНСТВО МОРСКОГО И РЕЧНОГО ТРАНСПОРТА
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ВОДНЫХ КОММУНИКАЦИЙ»
Васин А.В.
Интегральные уравнения.
Рекомендовано редакционно-издательским советом Санкт-Петербургского Государственного университета водных коммуникаций
Санкт-Петербург
2011 г.
УДК 517.7
ББК
Рецензенты
Кандидат физико-математических нау доцент Гулевич Н.М.
доктор технических наук, профессор Нырков А.П.
Васин А.В.
Интегральные уравнения: конпект лекций –СПб:СПБГУВК, 2011.-23 стр.
Учебно-методическое пособие содержит основной теоритический материал и конкретные примеры по дисциплине «Интегральные уравнения», и соответствует рабочим программам дисциплины, стандартам, указанной специальности, и может быть использовано при подготовке к экзамену студентами и преподавателями.
Предназначен для студентов четвертого курса (8-ой семестр) специальности 010501.65 «Прикладная математика и информатика».
УДК 517.7
ББК
Васин А.В, 2011
СПБГУВК, 2011
Интегральные уравнения Вольтерра
Основные понятия
Уравнение
где
–
известные функции, 
– искомая функция, 
– числовой параметр, называется линейным
интегральным уравнением Вольтерра 2-го
рода.
Функция
называется ядром
уравнения
Вольтерра. Если 
,
то уравнение (1) принимает вид
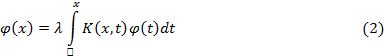
и называется однородным уравнением Вольтерра 2-го рода.
Уравнение
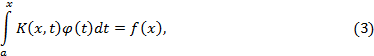
где
– искомая функция, называют интегральным
уравнением Вольтерра 1-го рода.
Не нарушая общности, можем считать
нижний предел 
равным нулю, что мы и будем предполагать
в дальнейшем.
Решением
интегрального уравнения (1), (2) или (3)
называют функцию
,
которая, будучи подставлена в это
уравнение, обращает его в тождество (по
).
Связь между линейными дифференциальными уравнениями и интегральными уравнениями Вольтерра
Решение линейного дифференциального уравнения
с
непрерывными коэффициентами 
(
при начальных условиях
может быть сведено к решению интегрального уравнения Вольтерра 2-го рода.
Покажем это на примере дифференциального уравнения 2-го порядка
Полагаем
Отсюда, принимая во внимание начальные условия (2’), последовательно находим
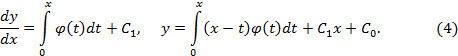
При этом мы использовали формулу
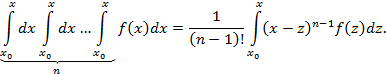
Учитывая (3) и (4), дифференциальное уравнение (1’) запишем так:
или
Полагая
приведем (5) к виду
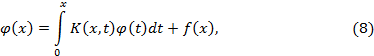
т.е. придем к интегральному уравнению Вольтерра 2-го рода.
Существование
единственного решения уравнения (8)
следует из существования и единственности
решения задачи Коши (1’) - (2’) для линейного
дифференциального уравнения с непрерывными
коэффициентами в окрестности точки 
И
наоборот, решая интегральное уравнение
(8) с 
и 
,
определенными по формулам (6) и (7), и
подставляя выражение, полученное для
,
в последнее из уравнений (4), мы получим
единственное решение уравнения (1’),
удовлетворяющее начальным условиям
(2’).
Задача 1. Составить интегральное уравнение, соответствующее дифференциальному уравнению
и начальным условиям
Решение. Полагаем
Тогда
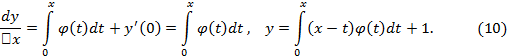
Подставляя (9) и (10) в данное дифференциальное уравнение, найдем
или
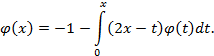
Резольвента интегрального уравнения Вольтерра
Определение резольвенты
Пусть имеем интегральное уравнение Вольтерра 2-го рода
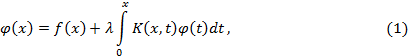
где
есть непрерывная функция при 
а 
непрерывна при 
.
Будем искать решение интегрального уравнения (1) в виде бесконечного степенного ряда по степеням :
Подставляя формально этот ряд в (1), получим
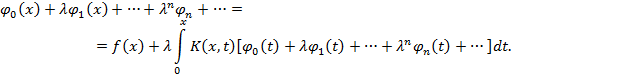
Сравнивая коэффициенты при одинаковых степенях , найдем
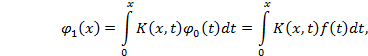
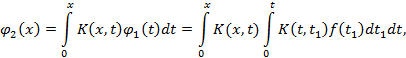
Соотношения
(3) дают способ последовательного
определения функций 
.
Можно показать, что при сделанных
предположениях относительно
и
полученный таким образом ряд (2) сходится
равномерно по
и
при любом
и 
и его сумма есть единственное решение
уравнения (1).
Далее, из (3) следует:
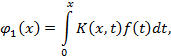
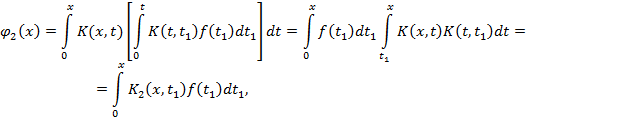
где
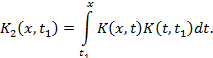
Аналогично устанавливается, что вообще
Функции
называются повторными
или итерированными
ядрами.
Они, как нетрудно показать, определяются
при помощи рекуррентных формул
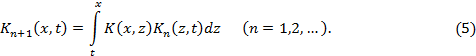
Используя (4) и (5), равенство (2) можно записать так:
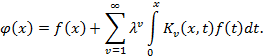
Функция
,
определяемая при помощи ряда
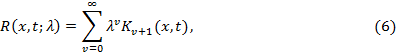
называется резольвентой (или разрешающим ядром) интегрального уравнения (1). Ряд (6) в случае непрерывного ядра сходится абсолютно равномерно.
Повторные ядра, а также резольвента не зависят от нижнего предела в интегральном уравнении.
Резольвента
удовлетворяет следующему функциональному
уравнению:
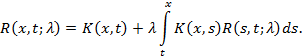
С помощью резольвенты решение интегрального уравнения (1) запишется в виде
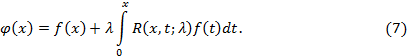
Нахождение резольвенты
Задача
2.
Найти резольвенту интегрального
уравнения Вольтерра с ядром 
.
Решение.
Имеем 
Далее, согласно формулам (5)
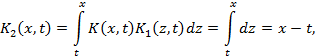
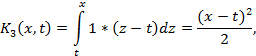
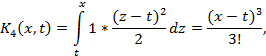
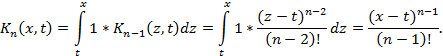
Таким образом, согласно определению
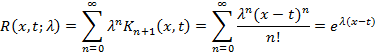
Соотношения
(3) дают способ последовательного
определения функций 
Можно показать, что при сделанных
предположениях относительно 
полученный таким образом ряд (2) сходится
равномерно по 
при любом 
и его сумма есть единственное решение
уравнения (1).
Далее, из (3) следует:
где
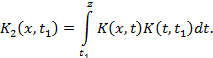
Аналогично устанавливается, что вообще
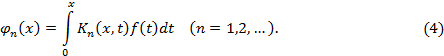
Функции называются повторными или итерированными ядрами. Они, как нетрудно показать, определяются при помощи рекуррентных формул
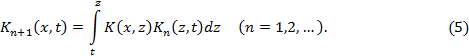
Используя (4) и (5), равенство (2) можно записать так:
