
ЛАБОРАТОРНАЯ РАБОТА 3 «Линейные групповые коды»
Цель работы: Исследовать построение и возможности корректирования линейных систематических групповых кодов.
Методика выполнения задания :
1.Выбор варианта.
j1 =ДАТА рождения – соответствует позиции ошибочного символа и равна mod n (cумма цифр) – для задания№1 и №3;
j2 = ГОД рождения– соответствует позиции ошибочного символа и равна mod n (cумма цифр) – для задания №2;
ВНИМАНИЕ n- количество информационных символов в задании
j3= Порядковый номер по списку - соответствует из варианту задания.
Лабораторная работа состоит из трех заданий.
Исходными данными являются:
для задания № 1 – информационное слово, производящая матрица G(n,k).\
для задания №2 – информационное слово, последовательность чисел;
для задания № 3 – информационное слово, код Хэмминга (n,k).
Выходные данные: показать процесс кодирования, декодирования и исправления одиночной ошибки для передаваемого информационного слова.
2.Теоретическая часть
По теореме Шеннона существует возможность вести передачу данных по каналу с помехами со сколь угодно малой вероятностью ошибки при подходящих процедурах кодирования и декодирования. Надежность передачи сообщений повышается за счет введения избыточности - слов, которые существуют, но не передаются. При этом каждому сообщению ставится в соответствие кодовое слово. Общая структура системы передачи данных приведена на рисунке.

Корректирующие свойства кода обычно описываются расстояниями между кодовыми словами. Вес Хемминга (кодовое расстояние) кодового слова определяется как число ненулевых компонентов данного кодового слова при использовании линейных кодов. Для обнаружения производимых искажений, которые изменяют в передаваемых кодовых блоках не более t символов, необходимо, чтобы никакие t-кратные искажения не переводили одно кодовое слово в другое, то есть необходимо, чтобы все кодовые слова находились друг от друга на расстоянии, большем t. Для исправления t-кратных ошибок необходимо, чтобы все кодовые слова находились на расстоянии, большем, чем (2*t+1). Задача построения кода сводится к выбору из множества всех кодовых слов подмножества разрешенных кодовых слов с заданным минимальным расстоянием Хемминга между ними.
3. Пример расчета
ЗАДАНИЕ 1.
Производящая матрица имеет вид:
 .
.
Определим комбинации корректирующего кода.
Для заданного числа информационных разрядов k = 4,число кодовых комбинаций равно N = 2k = 24 = 16.
1) 0000 5) 0010 9) 0001 13) 0011
2) 1000 6) 1010 10) 1001 14) 1011
3) 0100 7) 0110 11) 0101 15) 0111
4) 1100 8) 1110 12) 1101 16) 1111
Старшинство разрядов принимаем слева на право, в соответствии с их поступлением на вход декодера. Находим корректирующие разряды для каждого информационного слова, как результат суммирования по модулю два строк проверочной матрицы номера, которых совпадают с номерами единиц в информационных разрядах кода.
Например, для информационного слова I= [1001] кодовое слово имеет вид
 .
.
Строим код:
1) 0000 000 5) 0010 110 9) 0001 101 13) 0011 011
2) 1000 111 6) 1010 001 10) 1001 010 14) 1011 100
3) 0100 011 7) 0110 101 11) 0101 110 15) 0111 000
4) 1100 100 8) 1110 010 12) 1101 101 16) 1111 111
Декодирование по синдрому. Процесс декодирования осуществляется с помощью проверочной матрицы H. Для построенного (7, 4)-кода проверочная матрица имеет вид
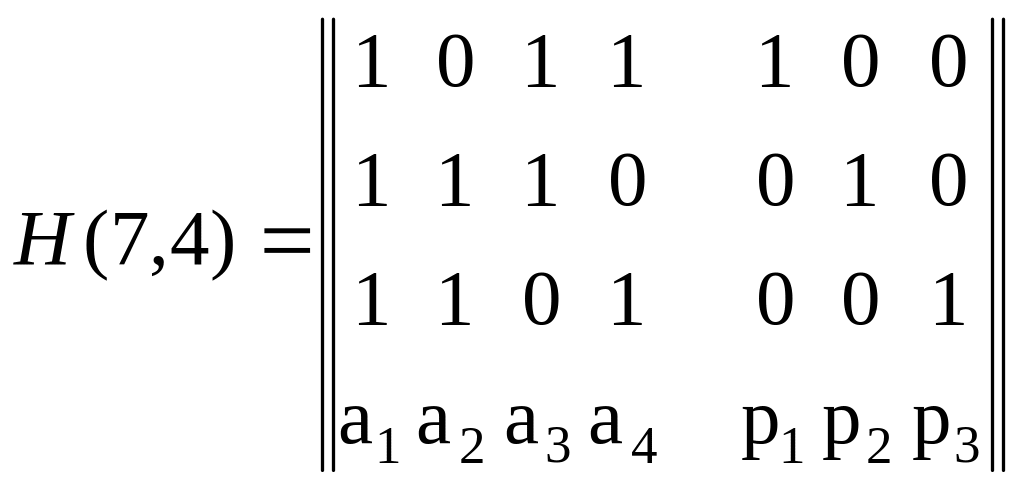 .
.
Строки проверочной матрицы определяют правила формирования проверок, позволяющие определить синдром ошибки.
 Пусть в процессе передачи произошла
ошибка во 2-м информационном разряде
Пусть в процессе передачи произошла
ошибка во 2-м информационном разряде
1 1 0 1 1 0 0 1
В соответствии с проверочной матрицей составляем проверочные векторы
p1a1a2a4 =S1 = 0110 = 0;
p2a1a2a3 =S2 = 0111 = 1 ;
p3a1a3a4 =S3 = 1101 = 1.
Синдром 011 показывает, что ошибка произошла во 2-м информационном разряде, который необходимо проинвертировать.
. ЗАДАНИЕ 2. (метод Хэмминга)
Построить код Хэмминга для передачи кодовой комбинации 1 1 0 1 1 0 1 1.
По заданной длине информационного слова (k = 8), используя соотношения вычислим основные параметры кода n и m.
m = [log2 {(k+1)+ [log2(k+1)]}]=[log2 {(9+1)+ [log2(9+1)]}]=4,
при этом n = k+m = 12, т. е. получили (12, 8)-код.
Определяем номера рабочих и контрольных позиции кодовой комбинации. Номера контрольных позиций выбираем по закону 2i .
Для рассматриваемой задачи (при n = 12) номера контрольных позиций равны 1, 4, 8.
При этом кодовая комбинация имеет вид:
b1 b2 b3 b4 b5 b6 b7 b8 b9 b10 b11 b12
к1 к2 1 к3 1 0 1 к4 1 0 1 1
. Определяем значения контрольных разрядов (0 или 1) путем многократных проверок кодовой комбинации на четность. Количество проверок равно m = n-k. В каждую проверку включается один контрольный и определенные проверочные биты.
Номера информационных бит, включаемых в каждую проверку определяется по двоичному коду натуральных n-чисел разрядностью - m.
Запишем проверочную матрицу H как ряд возрастающих чисел, начиная с 1.
H=
![]()
Количество разрядов m - определяет количество проверок на четность.
1) b1 b3 b5 b7 b9 а11 = b111111 =>
четная при b1=1
2) b2 b3 b6 b7 b10 b11 = b210101 =>
четная при b2=1
3) b3 b5 b6 b7 b12 = b31011=>
четная при b3=1
4) b4 b9 b10 b11 b12 = b41011 =>
четная при b4=1
Передаваемая кодовая комбинация: 1 2 3 4 5 6 7 8 9 10 11 12
1 1 1 1 1 0 1 1 1 0 1 1
Допустим, принято: 1 1 1 1 0 0 1 1 1 0 1 1
Для обнаружения и исправления ошибки составим аналогичные проверки на четность контрольных сумм, результатом которых является двоичное (n-k) -разрядное число, называемое синдромом и указывающим на положение ошибки, т. е. номер ошибочной позиции.
1) b1 b3 b5 b7 b9 b11 = 110111 =1
2) b2 b3 b6 b7 b10 b11 = 110101 =0
3) b3 b5 b6 b7 b12 = 10011 =1
4) b4 b9 b10 b11 b12 = 11011 =0
Вывод: синдром S = |1010|
Обнаружена ошибка: вектор ошибки E = | 0 0 0 0 1 0 0 0 |, указывает на ошибку в пятом разряде (обнаружена ошибка в позиции x5) . Для исправления ошибки необходимо инвертировать 5 -й разряд в кодовой комбинации.
