МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

Севастопольский национальный технический университет

Методические указания

к выполнению лабораторной работы

«ВЫЧИСЛЕНИЕ ОПРЕДЕЛЁННЫХ ИНТЕГРАЛОВ.

МЕТОД ТРАПЕЦИЙ »

по дисциплине «Вычислительные методы»

для самостоятельной работы студентов специальности

7.0914.01 «Системы управленияи автоматики»

Севастополь - 2003

В методических указаниях приведены описание лабораторной работы и варианты индивидуальных заданий к ней. Работа предназначена для приобретения практических навыков алгоритмизации и программирования на основе обобщённых квадратурных формул Ньютона-Котеса вычисления определенных интегралов. Работа ориентирована на применение метода трапеций и алгоритмических языков Паскаль и Си в среде операционной системы MSDOS.

Методические указания утверждены на заседании кафедры технической кибернетики, протокол № 8 от 16.06.2003

Методическое указание составил: ст. преп. Захаров В.В.

Рецензент: к.т.н., доцент Карапетьян В.А.

СОДЕРЖАНИЕ

1. Цель работы……………………..…………………..……………3

2. Обобщённые квадратурные формулы Ньютона-Котеса ….…..3

3. Метод трапеций ………………………………………………….5

4. Задание к работе………………………………….…..…….….…6

5. Оформление и содержание отчёта………………….…………...8

6. Контрольные вопросы…………………………….……………...9

7. Литература……………………………………….………………..9

Приложение 1…………………………………….……………….…...9

Приложение 2………………………………….…….………...……..11

1. Цель работы

1. Изучение численных методов вычисления определенных интегралов - обобщённых квадратурных формул Ньютона-Котеса.

2. Приобретение навыков алгоритмизации вычисления определенных интегралов на основе одной из обобщённых квадратурных формул Ньютона-Котеса - метода трапеций.

3. Приобретение навыков составления и применения подпрограмм вычисления определенных интегралов методом трапеций на языках Паскаль и Си.

2. Обобщённые квадратурные формулы ньютона-котеса

Настоящая работа посвящена реализации на ПК численных методов Ньютона-Котеса приближенного вычисления определённых интегралов

J = dx . (1)

и экспериментальному исследованию свойств этих методов. Вид подынтегральной функции f(x), а также значения нижнего a и верхнего b пределов интегрирования, определяются при проведении исследований вариантом индивидуального задания. Варианты заданий приведены в таблице раздела «Приложение 1». Там же для каждого варианта приведены формулы, определяющие в аналитическом виде первообразные F(x) на интервале [a,b] функций f(x). Знание первообразных позволяет при проведении экспериментов на ПК для заданного варианта f(x) вычислить точное значение интеграла (1)

J = dx = F(b) – F(a) (2)

и, сравнив его с полученными на основе нескольких методов Ньютона-Котеса приближенными значениеми интеграла (1), определить величины погрешностей этих методов.

Методы Ньютона-Котеса [1-3] относятся к интерполяционным численным методам вычисления определённых интегралов (методам численного интегрирования). Общая идея построения обобщённых квадратурных формул (обобщённых квадратур) методов Ньютона-Котеса состоит в следующем [1,2].

Интервал интегрирования [a,b] разбивается на n отрезков [x_i,x_i+1] точками x_i[a,b] , i=1,2,…,n+1 , при этом

x₁ = a ,

x₂ = x₁+h₁ , (3)

…………..

x_n+1 = x_n+h_n = b ,

где

h_i = x_i+1-x_i , i = 1,2,…,n (4)

длина i- го отрезка разбиения или шаг интегрирования. В результате интеграл (1) представляется суммой интегралов J_i на отрезках разбиения:

J = = 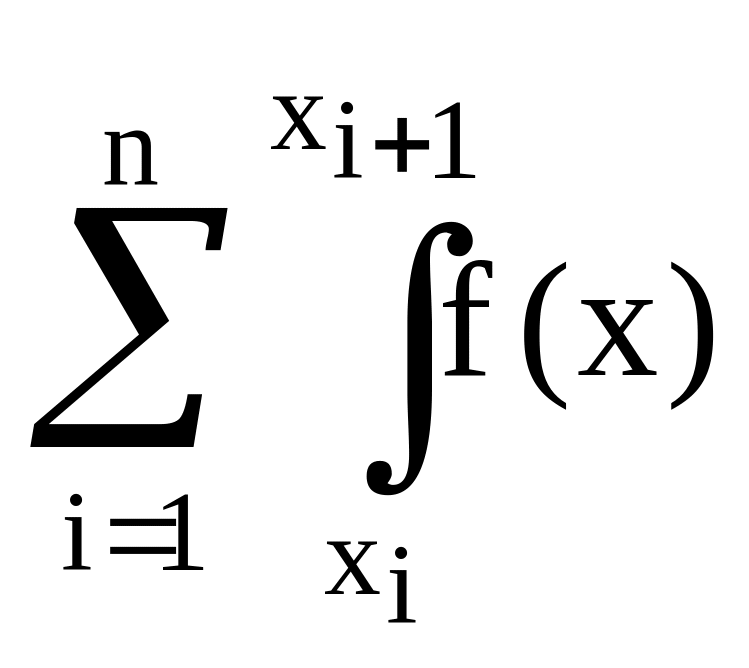dx . (5)

На каждом отрезке [x_i,x_i+1] подынтегральная функция f(x) заменяется интерполяционным полиномом (m-1)- вой степени, значения которого совпадают с значениями функции в m узлах интерполирования отрезка [x_i,x_i+1]. Число m определяет порядок метода. В качестве узлов интерполирования обычно выбираются точки x_i (3), либо середины отрезков [x_i,x_i+1]:

z_i = x_i +h_i /2 , i = 1,2,…,n . (6)

Далее интерполяционные полиномы интегрируются аналитически. В результате получаются приближенные формулы численного интегрирования, представляющие собой суммы значений подынтегральной функции в точках (3) и (или ) (5), умноженные на коэффициенты Котеса:

J  . (7)

Коэффициенты зависят только от шага интегрирования и порядка метода m.

Другой метод [3] получения обобщённых квадратур Ньютона-Котеса основывается на том, что приближённая формула (7) метода m - ого порядка позволяет вычислить точное значение интеграла (5) для подынтегральной функции f(x) суть полиномов по крайней мере до (m-1) - вой степени включительно. В качестве таких полиномов удобно взять полиномы вида:

f(x) = 1, (x-x_i) , (x-x_i)² ,…, (x-x_i)^m-1 ,

где i =1, 2,…, n . Тогда, приравнивая к нулю абсолютные погрешности вычисления на основе квадратур n интегралов J_i в (5)

E_i =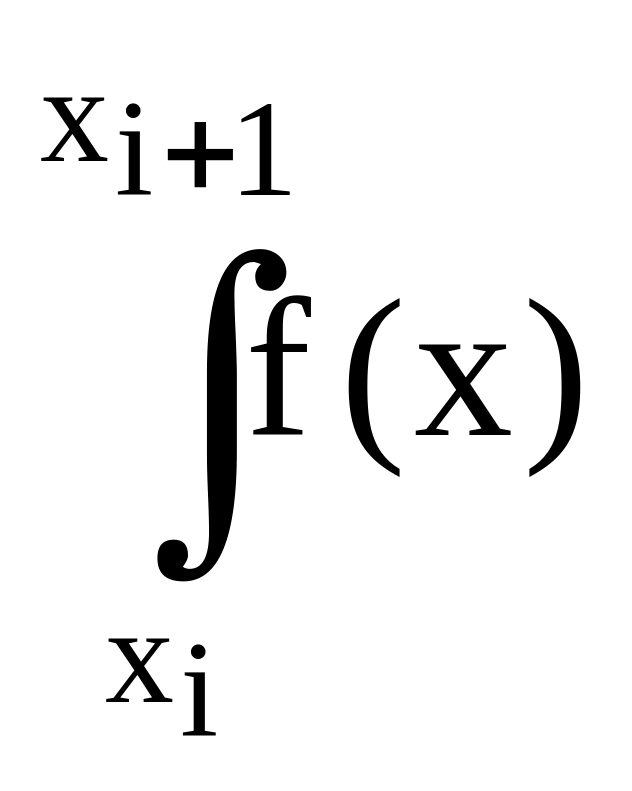 dx  , i = 1,2,…,n

для всех m представлений подынтегральной функции f(x) из (8), получают систему nm линейных алгебраических уравнений с nm неизвестными . При небольших значениях m её решение (искомые коэффициенты Котеса) легко находится аналитически, причём выбор больших значений m нецелесообразен по причине [1-3] снижения точности численного интегрирования.

Порядок метода m численного интегрирования не является однозначной характеристикой его точности. Точность квадратур обусловливается не только количеством m узлов итерполяции на отрезке [x_i,x_i+1] (степенью m-1 соответствующего интерполяционного полинома), но и способом их расположения на отрезке. Показано [1-3], что таким образом можно добится повышения степени полинома f(x), для которого квадратура дает точное значение интеграла, до степени 2m-3. Более адекватной характеристикой точности методов численного интегрирования является алгебраическая степень точности m_A метода. Число m_A равно максимальной степени полинома f(x), для которого квадратура точна. По величине m_A больше либо равна порядку метода m и зависит от расположении узлов интерполирования (3),(5).