- •5.1. Уравнение линии на плоскости
- •5.2. Уравнение поверхности и уравнения линии в пространстве
- •Виды уравнения прямой на плоскости
- •Неполные уравнения прямой. Уравнение прямой в отрезках.
- •Угол между двумя прямыми. Условия параллельности и перпендикулярности двух прямых.
- •Виды уравнения плоскости
- •Неполные уравнения плоскости. Уравнение плоскости в отрезках.
- •Пучки и связки плоскостей.
- •Прямая линия в пространстве
- •Условие принадлежности двух прямых к одной плоскости.
Неполные уравнения прямой. Уравнение прямой в отрезках.
Общее уравнение прямой (6.1) называется полным, если все его коэффициенты А, В и С отличны от нуля. Если хотя бы один из указанных коэффициентов равен нулю, уравнение называется неполным.
Рассмотрим все возможные виды неполных уравнений:
(1). С=0, уравнение Ах+Ву = 0 определяет прямую, проходящую через начало координат (поскольку координаты начала удовлетворяют этому уравнению).
(2). В=0, уравнение Ах+С=0 определяет прямую, параллельную оси Оу (поскольку нормальный вектор этой прямой n = (А, 0) ортогонален оси Оу).
(3). А = 0, уравнение Ву+С=0 определяет прямую, параллельную оси Ох (поскольку нормальный вектор этой прямой n = (0, В) ортогонален оси Ох).
(4). B = 0 и С=0, уравнение Ах = 0 определяет ось Оу (в самом деле, эта прямая параллельна оси Оу и проходит через начало координат).
(5). A = 0, С=0, уравнение Ву = 0 определяет ось Ох (ибо эта прямая параллельна оси Ох и проходит через начало координат).
Рассмотрим теперь полное уравнение прямой (6.1) и покажем, что оно может быть приведено к следующему виду:
 ,
(6.6)
,
(6.6)
называемому уравнением прямой в отрезках.
В самом деле, так как все коэффициенты А, В и С отличны от нуля, мы можем переписать уравнение (5.1) в виде
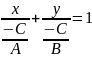
и затем положить
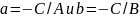 .
.
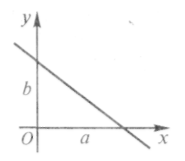
Замечание. В уравнении «в отрезках» (6.6) числа а и b имеют простой геометрический смысл: они равны величинам отрезков, которые отсекает прямая на осях Ох и Оу соответственно (отрезки отсчитываются от начала координат, см. рис.). Чтобы убедиться в этом, достаточно найти точки пересечения прямой, определяемой уравнением (6.6), с осями координат.
Уравнение прямой в форме «в отрезках» удобно использовать для построения этой прямой на чертеже.
Каноническое уравнение прямой. Любой ненулевой вектор, параллельный данной прямой, будем называть направляющим вектором этой прямой.
Задача: найти уравнение прямой, проходящей через заданную точку М1(х1,у1) и имеющей заданный направляющий вектор q = (l,m).
Точка М
(х, у) лежит
на указанной прямой тогда и только
тогда, когда векторы
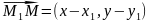 и q
= (l,m)
коллинеарны, т.е. тогда и только тогда,
когда координаты этих векторов
пропорциональны:
и q
= (l,m)
коллинеарны, т.е. тогда и только тогда,
когда координаты этих векторов
пропорциональны:
 (6.7)
(6.7)
Уравнение (6.7) и есть искомое уравнение прямой. Это уравнение называют обычно каноническим уравнением прямой.
Замечание.
В каноническом уравнении (6.7) один из
знаменателей l
или m
может оказаться равным нулю (оба числа
l
и
m
равняться
нулю не могут, поскольку вектор q
= (l,m)
ненулевой). Так как всякую пропорцию
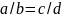 понимают как равенство
понимают как равенство
 ,
обращение в нуль одного из знаменателей
в (6.7) означает обращение в нуль и
соответствующего числителя. В самом
деле, если, например, l
= 0, то, поскольку m≠0,
из равенства
l(y-y1)
= m(х-х1)
заключаем, что х-х1=0.
,
обращение в нуль одного из знаменателей
в (6.7) означает обращение в нуль и
соответствующего числителя. В самом
деле, если, например, l
= 0, то, поскольку m≠0,
из равенства
l(y-y1)
= m(х-х1)
заключаем, что х-х1=0.
В заключение
запишем уравнение прямой, проходящей
через две заданные точки М1(х1,у1)
и М2(х2,у2)
(эти точки отличны друг от друга). Так
как за направляющий вектор такой прямой
можно взять вектор
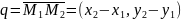 и прямая проходит через точку М1(х1,
у1),
то из канонического уравнения (6.6) получим
уравнение искомой прямой в виде
и прямая проходит через точку М1(х1,
у1),
то из канонического уравнения (6.6) получим
уравнение искомой прямой в виде
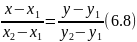
Параметрические уравнения прямой. Параметрические уравнения прямой получаются из канонического уравнения этой прямой. Примем за параметр t величину, стоящую в левой и в правой частях (6.7). Так как один из знаменателей (6.7) отличен от нуля, а соответствующий числитель может принимать какие угодно значения, то областью изменения параметра t является вся вещественная ось: -∞ < t < +∞.
Мы получим х - х1 = lt, у – у1 = mt или окончательно
x = x1 + lt, y = y1+ mt. (6.9)
Уравнения (6.9) и
есть искомые параметрические уравнения
прямой. Уравнения (6.9) допускают наглядную
механическую интерпретацию. Если
считать, что параметр t
— это время, отсчитываемое от некоторого
начального момента, то параметрические
уравнения (6.9) определяют закон движения
материальной точки по прямой линии с
постоянной скоростью
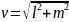 (такое движение происходит по инерции).
(такое движение происходит по инерции).
Прямая с угловым коэффициентом. Рассмотрим любую прямую, не параллельную оси Ох. Введем понятие угла наклона этой прямой к оси Ох. Предположим, что рассматриваемая прямая пересекает ось Ох в точке А (см. рис.). Возьмем на оси Ох произвольную точку М, лежащую по ту сторону от точки А, куда направлена ось Ох, а на рассматриваемой прямой произвольную точку N, лежащую по ту сторону от точки А, куда направлена ось Оу.
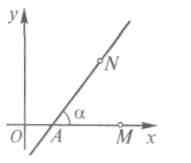
Угол
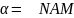 назовем углом наклона данной прямой к
оси Ох.
назовем углом наклона данной прямой к
оси Ох.
Если прямая параллельна оси Ох или совпадает с ней, то угол наклона этой прямой к оси Ох мы будем считать равным нулю.
Тангенс угла
наклона прямой к оси Ох
назовем угловым коэффициентом этой
прямой. Если обозначить буквой k
угловой коэффициент данной прямой, а
буквой α угол наклона этой прямой к оси
Ох,
то по определению можно записать
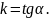
Замечание. Для прямой, параллельной оси Ох, угловой коэффициент равен нулю, а для прямой, перпендикулярной оси Ох, угловой коэффициент не существует (в последнем случае иногда говорят, что угловой коэффициент «обращается в бесконечность»).
Выведем уравнение прямой, проходящей через заданную точку М1(х1,у1) и имеющей заданный угловой коэффициент k.
Для этого докажем
сначала следующее утверждение: если
прямая не параллельна оси Оу и имеет
направляющий вектор q
=(l,m),
то угловой коэффициент этой прямой
равен
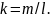
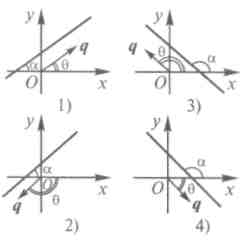
Пусть α — угол наклона прямой к оси Ох, а θ — угол наклона направляющего вектора q =(l,m) к оси Ох. Так как прямая может быть наклонена к оси Ох под острым или под тупым углом и ее направляющий вектор q может иметь два противоположных направления, то возможны четыре случая, изображенных на рисунке.
В случаях 1) и 3) θ = α и для проекций на оси вектора q справедливы формулы
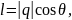
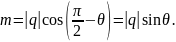
В случаях 2) и 4) θ = π-α и для проекций вектора q справедливы формулы
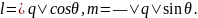
Таким образом, в
случаях 1) и 3)
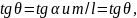 а в случаях 2) и 4)
а в случаях 2) и 4)
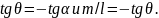
Поэтому, во всех
четырех случаях
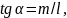 и утверждение доказано.
и утверждение доказано.
Для того чтобы
вывести уравнение прямой, проходящей
через заданную точку М1(х1,у1)
и имеющей заданный угловой коэффициент
k,
умножим обе части канонического уравнения
(6.7) на m
и учтем, что
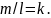
Получим искомое уравнение в виде
у-у1=k(х-х1). (6.10)
Если теперь обозначить через b постоянную b = у1-kх1, то уравнение (6.10) примет вид
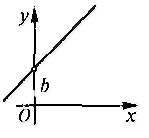
у = kх+b. (6.11)
Уравнение (6.11) называется уравнением прямой с угловым коэффициентом. В этом уравнении k обозначает угловой коэффициент данной прямой, a b представляет собой величину отрезка, отсекаемого данной прямой на оси Оу, начиная от начала координат. Чтобы убедиться в этом, достаточно рассмотреть совместно уравнение (6.11) и уравнение х = 0 оси Оу и найти координаты точки пересечения оси Оу и прямой (6.11): x=0, y = b (см. рис.).