УРАВНЕНИЕ ЛИНИИ НА ПЛОСКОСТИ. УРАВНЕНИЯ ПОВЕРХНОСТИ И ЛИНИИ В ПРОСТРАНСТВЕ

Лекция 5

Рассмотрим один из важнейших вопросов аналитической геометрии — вопрос об аналитическом представлении линии на плоскости и поверхности и линии в пространстве при помощи уравнений, связывающих их координат, а также простейшие задачи, связанные с таким аналитическим представлением. Приведем классификацию плоских линий и поверхностей. Докажем, что порядок алгебраической линии (и соответственно поверхности) не зависит от выбора декартовой прямоугольной системы координат.

5.1. Уравнение линии на плоскости

Предположим, что на плоскости заданы декартова прямоугольная система координат Оху и некоторая линия L. Рассмотрим уравнение, связывающее две переменные величины .

(5.1)

Определение. Уравнение (5.1) называется уравнением линии L (относительно заданной системы координат), если этому уравнению удовлетворяют координаты х и у любой точки, лежащей на линии L, и не удовлетворяют координаты х и у ни одной точки, не лежащей на линии L.

С точки зрения этого определения сама линия L представляет собой (в заданной системе координат) геометрическое место точек, координаты которых удовлетворяют уравнению (5.1)

Если в заданной системе координат урав­нение вида (5.1) является уравнением линии L, то говорят, что это уравнение определяет линию L.

Замечание. Нетрудно указать такое уравнение вида (5.1), которое либо определяет геометрический образ, отличный от того, что мы привыкли понимать под термином «линия», либо вообще не определяет никакого геометрического образа. Так, уравнение определяет на плоскости Оху лишь одну точку (0,0), а уравнение вообще не определяет никакого геомет­рического образа. Для того чтобы уравнение вида (5.1) опреде­ляло геометрический образ, отвечающий нашему привычному представлению о линии, следует подчинить функцию Ф(х,у) некоторым ограничениям (например, требова­нию однозначной разрешимости уравнения (5.1) относительно одной из переменных).

Пример. Уравнение

является уравнением окружности радиуса с центром в точке М₀(а, b). В самом деле, точка М(х, у) лежит на указанной окруж­ности тогда и только тогда, когда расстояние между точками М(х, у) и М₀(а, b) равно , т.е. тогда и только тогда, когда квад­рат расстояния между указанными точками ра­вен . Таким образом, координаты любой точки М(х,у), лежа­щей на указанной окружности, удовлетворяют уравнению (5.2), а координаты любой точки, не лежащей на указанной окружно­сти, не удовлетворяют уравнению (5.2).

Уравнение окружности радиуса с центром в начале коор­динат имеет более простой вид, а именно

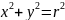(5.3)

Параметрическое представление линии. Для аналитического представления линии L часто бывает удобно выражать перемен­ные координаты х и у точек этой линии при помощи третьей вспомогательной переменной (или параметра) t:

(5.4)

где функции предполагаются непрерывными по па­раметру t в некоторой области изменения этого параметра.

Исключение из двух уравнений (5.4) параметра t приводит к рассмотренному выше уравнению вида (5.1).

Параметрическое представление линии на плоскости естествен­но возникает, если эту линию рассматривать как путь, пройден­ный материальной точкой, непрерывно движущейся по опреде­ленному закону. В самом деле, если переменная t представляет собой время, отсчитываемое от некоторого начального момента, то задание закона движения и представляет собой задание коор­динат х и у движущейся точки как некоторых непрерывных функ­ций времени t.

Пример 1. Установим параметрические уравнения ок­ружности радиуса с центром в начале координат. Пусть М(х, у) — любая точка этой окружности, а угол между радиу­сом-вектором ОМ и осью Ох, отсчитываемый против часовой стрелки (см. рис.). Очевидно, что

(5.5)

Уравнения (5.5) и представляют собой параметрические уравне­ния рассматриваемой окружности. Параметр t может принимать любые значения, но для того, чтобы точка М(х, у) один раз обо­шла окружность, следует ограничить область изменения пара­метра полусегментом . Заметим, что для исключения па­раметра t из уравнений (5.5) достаточно возвести в квадрат и сложить эти уравнения; мы получим при этом уравнение (5.3).

Замечание. Часто линию L определяют не уравнением (5.1), а разрешенным (например, относительно у) уравнением

y=f(x). (5.6)

Это уравнением представляет собой частный случай параметрического опре­деления этой линии (при x=t, у = f (t)).

Вид урав­нения линии L зависит не только от вида самой линии L, но и от выбора системы координат. Уравнение линии меняется как при переходе от одной декартовой системы координат к дру­гой, так и при переходе от декартовых к каким-нибудь другим координатам.

Если (5.1) представляет собой уравнение линии L относи­тельно декартовой прямоугольной системы координат Оху, то, чтобы получить уравнение той же линии L относительно другой системы координат, достаточно подставить в (5.1) на место х и у их выражения через новые координаты.

Так, например, линия L, определяемая в декартовой системе Оху уравнением (5.1), в полярной системе координат будет определяться уравнением

где введено обозначение Ф₁(ρ, φ) = Ф (ρ cos φ, ρsin φ).

Использование для определения некоторых линий недекарто­вых систем координат объясняется тем, что уравнение линии имеет при этом более простой вид.

В связи с аналитическим представлением линии возника­ют задачи двух типов. Задачи первого типа заключаются в изучении свойств линии при помощи заранее данного уравнения этой линии. Такое изучение проводится средствами математического анализа.

Задачи второго типа заключаются в выводе уравнения линии, зара­нее заданной геометрически (например, линии, заданной как гео­метрическое место точек, удовлетворяющих некоторым условиям).

Исходя из аналитического представления линий в декартовых прямоугольных системах координат, устанавливают следующую классификацию плоских линий.

Определение. Линия называется алгебраической, если в некоторой декартовой прямоугольной системе координат она определяется уравнением

(5.1)

в котором функция Ф (х, у) представляет собой алгебраический по­лином (сумму конечного числа слагаемых вида а_klх^kу^l, где к и l — целые неотрицательные числа, а_kl — некоторые постоянные).

Определение. Всякая неалгебраическая линия называется трансцендентной.

Определение. Алгебраическая линия называется линией по­рядка п, если в некоторой декартовой прямоугольной системе коор­динат эта линия определяется уравнением (5.1), в котором функция Ф (х, у) представляет собой алгебраический полином п-й степени.

Иными словами, линией п-го порядка называется линия, оп­ределяемая в некоторой декартовой прямоугольной системе ал­гебраическим уравнением степени п с двумя неизвестными.

Для корректности последних трех определений необхо­димо доказать следующее утверждение.

Теорема 5.1. Если линия в некоторой декартовой прямоугольной системе координат определяется алгебраическим уравнением сте­пени п, то эта линия и в любой другой декартовой прямоугольной системе координат определяется алгебраическим уравнением той же степени п.

Примером алгебраической линии второго порядка мо­жет служить окружность (уравнение (5.3) которой в некоторой декартовой прямоугольной системе является алгебраическим уравнением второй степени).

Замечание. Будем называть алгебраическую линию L распадающейся, если алгебраический полином Ф (х, у) степени п ≥ 2, стоящий в левой части уравне­ния этой линии, распадается на произведение Ф₁(х, у) · Ф₂(х,у) двух алгебраи­ческих полиномов Ф₁(х,у) и Ф₂(х,у) степеней к≥ 1 и п - к≥ 1, соответственно.

Из равенства Ф(х, у) = Ф₁(х, у) · Ф₂(х, у) очевидно, что координаты х и у точ­ки М удовлетворяют уравнению Ф(х,у) = 0 тогда и только тогда, когда эти коор­динаты удовлетворяют хотя бы одному из уравнений Ф₁(х, у) = 0 или Ф₂(х, у) = 0. Это означает, что линия L, определяемая уравнением Ф(х,у)=0, распадается на две линии: линию L₁, определяемую уравнением Ф₁(х, y) = 0, и линию L₂, определяемую уравнением Ф₂(х, у) = 0.

Так, линия четвертого порядка, определяемая уравнением

х⁴ + y⁴ + 2х²у² – 5x² - 5у² + 4 = (х² + у² - 1) (х² + у² - 4) = 0,

распадается на две окружности, определяемые уравнениями х² + у² - 1 =0 и х² + у² - 4 = 0.

Линия четвертого порядка, определяемая уравнением

х⁴ + у⁴ + 2x² у² - 2х²- 2у² + 1=(х² + у ²- 1)² = 0,

распадается на две «слившиеся» окружности, определяемые уравнением второго порядка х² + у² - 1 = 0. В отношении этой последней линии следует договориться, какое из чисел 2 или 4 мы будем понимать под ее порядком.

Важную роль в аналитической геометрии играет задача о нахождении точек пересечения двух произвольных линий L₁ и L₂, определяемых уравнениями Ф₁(х,y) = 0 и Ф₂(х,y) = 0, соответственно. Так как искомые точки пересечения в случае, если они существуют, должны одновре­менно лежать как на линии L₁, так и на линии L₂, то координаты этих точек должны удовлетворять каждому из уравнений Ф₁(х,y) = 0 и Ф₂(х,у) = 0.

Таким образом, для нахождения координат всех точек пересе­чения следует решить систему уравнений

Ф₁(х, у) = 0, Ф ₂(х,у) = 0. (5.7)

Каждое решение системы (5.7) определяет точку пересече­ния линий L₁ и L₂. Если система (5.7) не имеет решений, то линии L₁ и L₂ не пересекаются.

Так, для нахождения точек пересечения двух окружностей, определяемых уравнениями х² + у² = 1 и (х- 1)² + у² = 2, решаем си­стему уравнений

х² + у²-1=0, (х-1)²+у²-2 = 0. (5.8)

Вычитая из первого уравнения (5.8) вто­рое, получим 2х = 0, откуда х = 0. Вставляя это значение х в первое уравнение, най­дем, что у=±1. Получаем две точки пере­сечения М₁(0, 1) и М₂(0,-1) (см. рис. ).

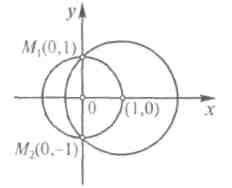
Замечание. Если L₁ и L₂ — две нераспадающиеся алгебраические линии порядков т и n со­ответственно и если одна из этих линий не содержится целиком в другой, то эти линии имеют не бо­лее чем т× п точек пересечения.