Діофантові рівняння

План

І. ВСТУП.

ІІ. ДІОФАНТОВІ РІВНЯННЯ.

ІІ.1 ЛІНІЙНІ ДІОФАНТОВІ РІВНЯННЯ.

ІІ.2 ВИВЕДЕННЯ ФОРМУЛ ЗАГАЛЬНОГО РОЗВ’ЯЗКУ ДІОФАНТОВОГО РІВНЯННЯ.

ІІІ. ЗНАХОДЖЕННЯ ЧАСТКОВОГО РОЗВ’ЯЗКУ ДІОФАНТОВОГО РІВНЯННЯ.

ІІІ.1 ЗНАХОДЖЕННЯ ЧАСТКОВОГО РОЗВ’ЯЗКУ ДІОФАНТОВОГО РІВНЯННЯ ЗА ДОПОМОГОЮ ЛАНЦЮГОВИХ ДРОБІВ.

ІІІ.2 ПРИКЛАДИ ЗНАХОДЖЕННЯ ЧАСТКОВОГО РОЗВ’ЯЗКУ ДІОФАНТОВОГО РІВНЯННЯ ЗА ДОПОМОГОЮ ЛАНЦЮГОВИХ ДРОБІВ.

ІІІ.3 ЗНАХОДЖЕННЯ ЧАСТКОВИХ РОЗВ’ЯЗКІВ ОКРЕМИХ ВИДІВ ДІОФАНТОВИХ РІВНЯНЬ.

IV. ЗАСТОСУВАННЯ ФОРМУЛ ДЛЯ ЗНАХОДЖЕННЯ НУЛЬОВОГО РОЗВ’ЯЗКУ ДІОФАНТОВОГО РІВНЯННЯ ДО РОЗВ’ЯЗУВАННЯ РІВНЯНЬ З ЦІЛОЮ І ДРОБОВОЮ ЧАСТИНАМИ.

V.ПРИКЛАДИ ЗАСТОСУВАННЯ АЛГОРИТМУ ЕВКЛІДА ДО РОЗВ’ЯЗУВАНЯ ДІОФАНТОВИХ РІВНЯНЬ.

ВИСНОВОК

Діофантові рівняння були названі по імені відомого грецького математика Діофанта, який жив у ІІІ або IV столітті до нашої ери . Про життя цього вченого ми майже нічого не знаємо, крім фактів описаних в арифметичній задачі, складеній у поетичній формі. Але його праці говорять про нього як про талановиту і цікаву людину. Окремі діофантові рівняння були відомі ще у давні часи. Загальні розв’язки рівняння були описані також у працях Евкліда. Формули, які дають цілі розв’язки рівняння з цілими числами,розглядалися також стародавніми індуськими математиками. Це говорить про те, що ця тема є важливою і цікавою.

Протягом навчання в гімназії ми систематично розв’язуємо рівняння – спочатку найпростіші, так звані лінійні рівняння, а потім квадратні – показникові, логарифмічні, тригонометричні не тільки з одним,а й з кількома невідомими, ознайомлюємось також із найпростішими системами рівнянь.

Така увага до рівнянь пояснюється не лише тим, що розв’язувати їх дуже цікаво. Хоча й цей аспект дуже важливий: пошуки розв’язку нестандартного рівняння розвивають кмітливість, виховують настирливість, збагачують досвід. Але головним є те, що рівняння здебільшого виникають як результат суто математичного пере формулювання і запису задач найрізноманітнішого змісту. Ї походження.

Зокрема, саме до рівнянь зводяться численні задачі з геометрії, фізики, хімії, математичного аналізу та інших галузей науки й практики. Саме ця обставина спонукала математиків насамперед займатися розробкою методів розв’язування різних типів рівнянь, і вона повністю виправдовує зусилля спрямованні на оволодіння цими методами.

Розв’язки деяких рівнянь – це вже не окремі числа, а впорядковані набори стількох чисел, скільки невідомих містить рівняння. Наприклад, упорядковані пари чисел (2;-1), (-π; ) є розв’язками рівняння х+2у=0 з двома невідомими, а впорядковані трійки чисел (1;1; ),(-3;4;-5) розв’язками рівняння з трьома невідомими. Як і у випадку рівнянь з одним невідомим, досить часто доводиться шукати не всі розв’язки рівняння: якщо ми знатимемо всі розв’язки, то після цього зможемо виявити серед них, які мають потрібну додаткову властивість. Проте насправді все значно складніше. Розглянемо, наприклад, рівняння з трьома невідомими х, у, z . Знайти всі його дійсні розв’язки дуже легко. Трійка дійсних чисел (а; в; с) тоді тільки буде розв’язком цього рівняння, коли с= або с , причому числа а, в – будь-які. Отже рівняння має безліч розв’язків, причому попереднє рівняння повністю описує множину всіх його розв’язків. Уявимо тепер, що нам треба знайти ті розв’язки (а; в; с) даного рівняння, у яких а, в і с – натуральні числа. Будемо називати їх коротко натуральними розв’язками. Задача ця виникає цілком природно, її можна, наприклад, тлумачити геометрично: знайти всі можливі прямокутні трикутники, у яких сторони вимірюються цілими числами. Зовсім не видно, проте, як для розв’язання цієї задачі можна використати наші знання про всі дійсні розв’язки рівняння. Можна, звичайно, сформулювати відповідь так: «Натуральними розв’язками даного рівняння будуть всі трійки а; в; , у яких а і в – довільні натуральні числа, але такі, щоб також було натуральним числом». Але таку відповідь аж ніяк не можна вважати прийнятною, бо це все одно що сказати: «Натуральними розв’язками рівняння будуть всі ті трійки (а; в; с), у яких а, в, с – натуральні числа, що задовольняють рівняння», тобто в неявній формі повторити умову.

Таким чином, задача відшукання натуральних розв’язків рівняння якісно відрізняється від задачі про відшукання всіх його дійсних розв’язків. Друга задача, як бачимо, досить проста, а розв’язання першої потребує певних зусиль і винахідливості.

Зауважимо, що розв’язування рівнянь у цілих (і, зокрема, натуральних) числах є однією з найстародавніших математичних задач. Уже на початку ІІ тисячоліття до н.е. вавилоняни вміли розв’язувати системи таких рівнянь з двома невідомими. Найбільшого розквіту ця галузь математики набула в Стародавній Греції. Основним джерелом для нас є «Арифметика» Діофанта (ІІІ до н.е.), де розглядаються різні типи рівнянь та систем з раціональними коефіцієнтами, розв’язки яких подаються у цілих (або раціональних) числах. Ці рівняння (та їх системи) називають діофантовими.

ІІ. ДІОФАНТОВІ РІВНЯННЯ

Діофантовими рівняннями називають алгебраїчні рівняння або системи алгебраїчних рівнянь з цілими коефіцієнтами, для яких треба знати цілі або раціональні розв’язки. При цьому число невідомих в рівняннях повинно бути не менше двох.

ІІ.1 ЛІНІЙНІ ДІОФАНТОВІ РІВНЯННЯ

Діофантові рівняння виду ах+bх=с, де а,b,с цілі числа, називають лінійними діофантовими рівняннями. Інколи їх називають діофантовими рівняннями першого степеня. Лінійні діофантові рівняння мають безліч розв’язків. Вони можуть бути відображені графічно або описані за допомогою формул.

Іі.2 виведення формул загального розв’язку діофантового рівняння

Загальний вид розв’язку діофантового рівняння має вигляд:

, де k € Z (1)

Розглянемо доведення формул (1)

Розглянемо діофантові рівняння ах+bх=с (2). Представимо його у вигляді y= x+ (3) і розглянемо лінійну функцію. Графіком цієї функції є пряма. Пряма що є графіком рівняння (3) нахилена до вісі ОХ під кутом тангенс якого дорівнює (мал. 1), а тангенс кута АРК дорівнює .

Нехай x₀ і y₀ є частковим розв’язком рівняння (2), а x_k і y_k довільний розв’язок цього рівняння. Розглянемо трикутник АВС, де АВ = y₀ - y_k, a BC=x_k - x₀ . Кут АСВ дорівнює куту АРК і відповідно тангенс кута АСВ дорівнює тангенсу кута АРК. У трикутнику АВС

tg кута АВС= = =

Де k € Z. Отримані формули (4) і є загальним розв’язком рівняння (2)

Мною розглянутий варіант коли пряма нахилена до вісі Ох під тупим кутом. Якщо кут нахилу гострий, то при виконанні аналогічних міркувань ми отримаємо ті самі результати.

Ііі. Знаходження часткового розв’язку діофантового рівняння

Розглянемо число і його ланцюговий дріб (a₀,a₁,…,a_n ).

Нескоротні дроби , , , … , є результатом похідних дробів порядку 1,2,…,n відповідно. Тоді для буде вірна формула

, де = останній похідний дріб до ланцюгового дробу, в яку розкладається дріб . Так як дроби і нескоротні, то P_n=aQ_n i aQ_n-1-bP_n-1=(-1)ⁿ . помноживши обидві частини на (-1)n маємо a((-1)nQn-1)+b((-1)n=qcPn-1)=c, таким чином пара чисел x0=(-1)ncQn-1, y0=(-1)n+1cPn-1 буде розв’язком рівняння (1).

Ііі.2 приклади знаходження часткового розв’язку діофантового рівняння за допомогою ланцюгових дробів

Приклад №1

Розв’язати рівняння в цілих числах 7х+12у=9 Знайдемо НСД(7;12)=1. Перевіримо умову 9М. Знайдемо нульовий розв’язок.

Для цього розглянемо дріб і розкладемо його в ланцюжковий дріб.

= =0+ =(0;1;1;2) Складемо всі підхідні дроби

На основі властивостей похідних дробів Pkqk-1 – Pk-1Qk=(-1)k-1 отримаємо 75-312-(-1)3; 75-312=-1‌ | (-9); 7(-45)+27 12 = 9.

Отже частковий розв’язок х₀=45 , у₀=27. Всі розв’язки можуть бути описані за допомогою формул

, де k€Z

Ііі.3 знаходження часткових розв’язків окремих видів діофантових рівнянь

Досить відомий варіант знаходження часткового розв’язку діофантового рівняння за допомогою ланцюжкових дробів. Цей метод досить відомий і простий, але вимагає багато нескладних розрахунків.

Розглядаючи перший варіант виведення формул загального розв’язку (2), описаний у цій роботі, можна запропонувати формули для знаходження часткових розв’язків окремих видів діофантових рівнянь.

Розглянемо на мал.1 трикутник АКР, де АК=у₀, КР=ОР – х_о Отже

tgАРК= = = = , де k€Z

Отже, у діофантовому рівнянні нульові розв’язки можна знайи за формулами (5)

Приклад №2.

Розв’яжіть діофантове рівняння

ax+by=c Знайдемо часткові розв’язки за формулами (5)

де k€Z →

Опишемо загальні розв’язки цього рівняння.

,де k€Z

Повернемося до мал.1. Розглянемо на ньому трикутник ДМА, де ДМ= – y, AД=х0, а кут МАД дорівнює куту АРК, отже

tg МАД= = = → 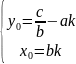, де k€Z. (6)

Отже, у діофантовому рівнянні нульовий розв’язок може бути знайдений за формулами (6).

Приклад №3

Знайдіть загальні розв’язки діофантового рівняння

11х+5у=15

Розв’язання

Знайдемо нульові розв’язки заданого рівняння за допомогою формул (4)

, де k€Z

Опишемо загальні розв’язки заданого рівняння за допомогою формул (4)

, де k€Z

Розглядають також лінійні діофантові рівняння з більшою кількістю невідомих. Якщо серед чисел а,в,с є принаймні два взаємно прості, то діофантове рівняння ах+ву=d–cz просто зводиться до рівняння з двома невідомими. Справді, припустивши, що взаємно простими є числа а та в дістанемо ах+ву=d–cz. Тоді для кожного цілого z ми матимемо нескінченне число розв’язків (х;у). При цьому елементи х₀ та у₀ частково розв’язку (х₀;у₀) виявляться функціями змінної z.

Якщо серед чисел а,в,с немає жодної пари взаємно простих, але найбільший спільний дільник усіх трьох чисел дорівнює 1, то для розв’язування ах+ву+cz=d поступають так. Нехай р – найбільший спільний дільник чисел а та в , тоді а=ра₁, в=рв₁ і задане рівняння набирає вигляду а₁х+в₁у= . Для того, щоб це рівняння мало розв’язки в цілих числах, необхідно, щоб дріб у його частині був цілим числом . Позначаючи d – cz = pn, матимемо: а₁х + в₁у = n , cz + pn = d , оскільки а₁ та в₁ взаємно прості, то х=х₀+в₁у=n, cz+pn=d. k€Z, причому х₀ та у₀ лінійно залежать від n. Оскільки с та р – теж взаємно прості, то рівняння cz+pn=d має розв’язки вигляду z=z₀+pn, n=n₀-cm, m€Z підставляючи значення n у формули для х та у, одержимо разом з формулою для z шукані розв’язки (x;y;z).

Приклад №4

Ров’язати в цілих числах рівняння 12х+15у+20z=181.

Розв’язання. Жодні два числа 12, 15, 20 не є взаємно простими, але найбільший спільний дільник усіх трьох чисел дорівнює 1. Отже, це рівняння має нескінченну кількість розв’язків у цілих числах. Запишемо його у вигляді 4x+5y= . Тоді 181-20z=3n. звідси маємо 20z+3n=181. Оскільки значення z₀=8 та n₀=7 задовольняють останнє рівняння, то z=8+3m, n=7-10m, m€Z. Отже, для визначення х,у,z дістаємо рівняння 4х+5у=7-20m. Одним із його розв’язків є х₀=3-5m, y₀=-1. Тому остаточно маємо: х=3-5m+5k, y=-1-4k, z=8+3m, де k€Z m€Z.

Ще одним прикладом діофантового рівняння є рівняння x²+y²=z² розв’язки якого є цілочисельними довжинами відповідно катетів та гіпотенузи у прямокутних трикутниках . Взаємно прості розв’язки цього рівняння знаходять за допомогою формул : x=m²-n², y=2mn, z=m²+n², де m,n – взаємно прості числа натуральні числа і m>n. Помножуючи кожен із цих розв’язків на натуральні числа k можна дістати всі розв’язки заданого рівняння .

Приклад №5

Знайти всі прямокутні трикутники з цілочисловими довжинами сторін, одна з яких дорівнює 1997.

Розв’язання. Сторони таких трикутників задовольняють співвідношення а²+в²=с² . Оскільки 1997 – просте число, то числа а,в,с мають бути попарно взаємно простими. Зрозуміло що 2mn≠1997. Якщо ж m²-n²=1997, то (m+n)(m-n)=1997, звідки m+n=1997, m-n=1. Отже, m=999, n=998, Якщо ж m²+n²=1997, то повним перебором по m€[1;р], де р=44 – ціла частина числа , знаходимо, що дану рівність при умові m>n задовольняють числа m=34, n=29. Отже, сторони шуканих трикутників є такими: 1997,2*999*998=1994004, 9992+9982=1994005 та 342 – 292 = 315, 2*34*29=1972, 1997.

Звичайно розв’язування діофантового рівняння значно спрощується, якщо його вдається звести до знаходження взаємно простих розв’язків. Наприклад, рівняння m²+n²=kmn при кожному фіксованому цілому k разом з парою (m;n) задовольняє також пара (mp;np), де р – довільне ціле число, і навпаки, якщо розв’язки m та n мають спільний дільник р, то після ділення обох цих чисел на р одержимо нову пару чисел, які теж є розв’язками даного рівняння. Якщо ж m та n – взаємно прості, то з рівняння випливає, що m² має ділитися на n, а n² на m. Зокрема, при натуральних m та n це можливо лише при m=n=1. Звідси одержуємо, що задане рівняння має розв’язки в натуральних числах лише при k=2. При цьому m=n , де n – довільне натуральне число.

Серед діофантових рівнянь другого степеня варто виділити рівняння вигляду х2-ky2=1, де k – довільне натуральне число. Зрозуміло, що пари (1;0) та (-1;0) є розв’язками даного рівняння при довільному k. Якщо k=n² , то дане рівняння можна записати у вигляді (x – ny)(x + ny)=1. Звідси х – ny=x+ny=±1, отже y=0. Інших цілочисельних розв’язків таке рівняння не має. При k ≠ n² можливі також інші розв’язки заданого рівняння. Оскільки разом з парою (х;у) його розв’язками є також пари (х;-у), (-х;-у), то обмежимося знаходженням розв’язків у натуральних числах . Для цього діємо таким чином. Запишемо дане рівняння у вигляді . Якщо (x₀;y₀) – один з його розв’язків, то (x₀+y₀ ) (x₀-y₀ )=1, а також (x₀+y₀ )²(x₀-y₀ )²=1. Оскільки останню рівність можна переписати у вигляді

(x₀+ky₀+2x₀y₀ )²(x₀+ky₀-2x₀y₀ )²

Звідки (x₀²+ky₀²)² – k(2x₀y₀)²=1 то пара (х1;у1) де х1=х20=ky20, y1=2x0y0, теж є розв’язком цього рівняння, причому х1>х0у1>у0. Аналогічно використовуючи співвідношення (x₀+y₀ )ⁿ(x₀-y₀ )ⁿ=1 , можна знайти нескінченну кількість розв’язків.

До того ж результату можна прийти і таким способом. Нехай (х0;у0) – один з розв’язків рівняння х2-ky2=1. Визначимо для натуральних n числа xn = x0xn-2+ky0yn-1, yn=y0xn-1+x0xn-1. Тоді x_n²+ky₀²=(x₀²+ky_0­y_n-1)²-k(x₀²+ky₀²)²-k(y₀x_n-1=x₀y_n-1)= =x²_n-1(x₀² - ky₀²)+ky²_n-1(ky₀²-x₀²)=x²_n-1 - ky²_{n-1 ­}.

Оскільки при n=1 маємо x²_n-1 - ky²_n-1 =1, то хвідси встановлюємо що при кожному натуральному n також справджується рівність x²_n-1 - ky²_n-1=1 .

Причому коли (х₀;у₀) – найменший розв’язок заданого рівняння у натуральних числах, то обома описаними вище способами одержимо всі розв’язки цього рівняння у натуральних числах. Подібними міркуваннями можна розв’язувати і деякі інші діофантові рівняння другого степеня.

Приклад №6

Скільки розв’язків у натуральних числах має рівняння х(х+1)=2у²? Розв’язання. Очевидно, що пара (1;1) є розв’язком даного рівняння . Покажемо, що коли х=а, у=b – розв’язок, то х=3а+4b+1, y=2a+3b+1 – також розв’язок.

Справді,(3а+4b+1)(3а+4b+2)-(3а+4b+1)²=

=9a²+12ab+6b+12ab+16b²+8b+3a+4b+2-2(4a²+9b²+112ab+4a+6b) =

=a²+a-2b²=a(a+1)-2b²=0

Оскільки 3a+4b+1>b , то множина розв’язків заданого рівняння у натуральних числах нескінченна.

Помноживши обидві частини рівняння із прикладу 3 на 4 , його можна було б записати у вигляді (2х+1)²-2(2у)²=1, а потім скористатися вище описаними методами для розв’язування рівняння вигляду t²-2z²=1. Звідси можна було б дістати також формули х=3а+4b+1, y=2a+3b+1. Пропоную читачам самостійно пересвідчитись, що разом із розв’язком х=а, y=b це рівняння задовольняють також числа x=a²+4a, (y=4a+2)b.

Як частковий випадок діофантових рівнянь можна розглядати рівняння, розв’язки яких пропонується знайти у простих числах. Звернемося до вже знайомого нам рівняння вигляду x² – ky²=1.

Приклад №7

Розв’язати у простих числах рівняння x² – 2y²=1.

Розв’язання. Зрозуміло, що х повинен бути непарним числом, тобто х=2р+1. Якщо y=2m+1,то x²-2y²=(2k+1)²-2(2m+1)²=4(k2+k+2m²2m)-1≠1. Отже, у повинен бути парним (і простим). Тому у=2. Легко пересвідчитись, що тоді х=3. Отже, х=3, у=2 – єдиний розв’язок заданого рівняння у простих числах.

Які ж загальні методи розв’язування діофантових рівнянь?

Насамперед, при розв’язуванні лінійного рівняння використовуємо подільність чисельника відповідного дробу на знаменник. Цей метод можна розглядати як частковий випадок методу остач, суть якого полягає в тому, що за наявності розв’язків у цілих числах остачі від ділення лівої та правої частини рівняння на одне і те ж натуральне число повинні бути однаковими. Наприклад, у прикладі були використані остачі від ділення на 2 для доведення непарності числа х та на 4 для доведення парності числа у.

Метод остач може бути використаний і при розв’язуванні інших рівнянь. Розглянемо приклади.

Приклад №8

Чи існують натуральні числа х,у які задовольняють рівняння х³-х=3у²+2003? Розв’язання. х3-х=(х-1)х(х+1). Отже, при цілих х ліва частина рівняння ділиться на 3 – як добуток трьох послідовних цілих чисел. Але 3у²+2003 при всіх цілих при діленні на 3 дає остачу 2. Тому задане рівняння не має розв’язків у натуральних числах.

Приклад №9

Знайти всі розв’язки рівняння 19х+97у=116z у натуральних числах.

Розв’язання. при натуральних z 2, права частина рівняння ділиться на 8. Оскільки 19=2*8+3, 97 = 12*8+3, а 32k при діленні на 8 дає остачу 1, 32k+1 – остачу 3, то 19х+97у при діленні на 8 може давати лише остачі 2 або 4. Отже, z 2. Оскільки далі, при х 2, у 2 виконуються нерівності 19х>116, 97у> 116, то х 2, у 2. Нарешті, легко перевірити, що трійка x=у=z=1 задовольняє дане рівняння, а, значить, є його єдиним розв’язком у натуральних числах.

При розв’язуванні прикладу 5 ми одержали рівняння вигляду m²+n²=1997. Для знаходження його розв’язків у натуральних числах було використано повний перебіг натуральних чисел з відрізка[1:44]. Отже, метод повного перебору теж заслуговує на увагу при поєднанні діофантових рівнянь. В окремих випадках він може поєднуватися з іншими методами. Зрозуміло, що такий метод застосований лише тоді, коли множини значень кожної з змінних є обмеженими і не надто об’ємними.

Для отримання розв’язків рівняння x2 – ky2=1 в одному із розглянутих вище способів був використаний розклад на множники.

Приклад №10

Знайти всі цілі числа х,у що є розв’язком рівняння x² – 4y²=1997.

Розв’язання. Запишемо задане рівняння у вигляді (х-2у)(х+2у)=1997. Оскільки 1997 – просте число, то приходимо до такої сукупності системи двох рівнянь.

х – 2у=1 х – 2у=1997 х – 2у=-1 х – 2у=-1997

х+2у=1997 х+2у=1 х+2у=-1997 х+2у=-1

З них відповідно знаходимо х=999;у=499, х=999;у=-499, х=-999; у=499, х=-999;у=499.

Звичайно, безпосередньому розкладу на множники можуть передувати тотожні перетворення. Розглянемо приклад Приклад №11.

Знайти всі натуральні числа х, у, що є розв’язком рівняння

ху – 3х + 5у =25.

Розв’язання. Задане рівняння можна записати у вигляді (х+5)(у-3)=10. Оскільки при натуральних х:х+5>5, а єдиним дільником числа 10, більшим за 5, є число 10, то х+5=10, у–3=1. Отже маємо єдиний розв’язок х = 5; у = 4.

Ще одним із методів розв’язування таких рівнянь є метод рекурентних формул.

У деяких випадках легко знайти один «очевидний», розв’язків ніяк не вдається відшукати. Та не завжди вони вони й існують. У таких випадках необхідно обґрунтувати єдність знайденого розв’язку. Умовно такий метод можна назвати методом єдності. Але при цьому, як правило, у кожному конкретному випадку доводиться проводити різні додаткові міркування, окремі з яких можна розглядати як як самостійні методи розв’язування діофантових рівнянь.

Приклад №12

Розв’язати у цілих числах рівняння x²+y²+z²-2x+4y-6z=-14.

Розв’язання. Перепишемо задане рівняння у вигляді (х-1)²+(у+2)²+(z-3)²=0.

Зрозуміло тепер, що х=1, у=-2, z=3 – єдиний розв’язок не лише в цілих, але й в дійсних числах.

Приклад №13

Знайти всі цілі числа x,y,z, що є розв’язком рівняння x³+3y³=9z³ .

Розв’язання. Очевидно, що трійка x=у=z=0 є розв’язком даного рівняння. Припустимо, що рівняння має інші цілочислові розв’язки. Тоді принаймні одне з чисел x,y,z відмінне віл нуля. Нехай р – найбільший спільний дільник чисел x,y,z. При цьому, якщо одне х цих чисел дорівнює нулю, то будемо вважати, що р – найбільший спільний дільник двох інших чисел. Два числа одночасно дорівнювати нулю не можуть, бо в такому випадку ми знову одержали б трійку x=у=z=0. Нехай x=px₁, y=py₁, z=pz₁. Тоді принаймні в одній парі чисел x₁, y₁, z₁ маємо два скорочення на р³ , що x₁³+3y₁³=9z₁³. Звідси x₁³, а за ним і х1 ділиться на 3. Отже, x₁=3x². Підставляючи це значення х в рівняння, після скорочення на 3 матимемо 9x₁³+y₁³+3z₁³. Аналогічним міркуванням встановлюємо, що y1=3y² i 3x₂³+9y₂³=z₁³. А тому z₁=3z². Отже, серед чисел x₁,y₁,z₁, немає жодної пари взаємно простих. Одержане протиріччя з припущенням доводить, що задане рівняння не має інших цілочислових розв’язків, крім x=у=z=0.

Такий метод доведення єдності розв’язку називається методом доведення від супротивного. Зауважимо, що він може бути використаний і для доведення відсутності розв’язків.