1. Последовательное соединение.

Выходной сигнал предшествующей системы является входным для последующей. Эквивалентная передаточная функция общей системы равна произведению передаточных функций систем, в нее входящих:

H(z) = H₁(z)H₂(z)...H_N(z).

Назад

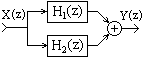
2. Параллельное соединение.

Сигнал подается на входы всех параллельно соединенных систем одновременно, выходные сигналы систем суммируются. Эквивалентная передаточная функция общей системы равна сумме передаточных функций систем, в нее входящих:

H(z) = H₁(z)+H₂(z)+...+H_N(z).

Назад

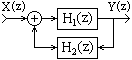
3. Соединение обратной связи.

Выходной сигнал первой системы подается на выход системы и одновременно на вход системы обратной связи, выходной сигнал которой суммируется, со знаком плюс или минус в зависимости от вида связи (отрицательной или положительной), с входным сигналом первой системы. Эквивалентная передаточная функция общей системы:

H(z) = H₁(z)/(1H₁(z)H₂(z)).

Назад

Схемы реализации систем.

По принципам структурной реализации систем различают следующие схемы:

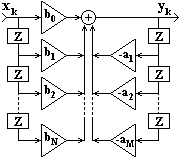
1. Прямая форма.

Реализуется непосредственно по разностному уравнению

y_k = b_nx_k-n - a_my_k-m,

или по передаточной функции

H(z) = b_nzⁿ /(1+ a_mz^m).

Пример прямой системы приведен на рис.

Назад

2. Прямая каноническая форма

содержит минимальное число элементов задержки.

v(k) = x(k) - a_mv(k-m), (9.6.1)

y(k) = b_nv(k-n). (9.6.2)

Граф реализации РЦС приведен на рисунке

Граф реализации РЦС приведен на рисунке

Назад

3. Каскадная (последовательная) форма.

Соответствует представлению передаточной функции в виде произведения:

H(z) =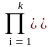 H_i(z).

H_i(z) - составляющие функции типа (1-r_iz)/(1-p_iz) при представлении H(z) в факторизованной форме, где r_i и p_i- нули и полюсы функции H(z). В качестве функций H_i(z) обычно используются передаточные функции биквадратных блоков - фильтров второго порядка:

H_i(z) = (b_0i+b_1iz+b_2iz²)/(1+a_1iz+a_2iz²).

Назад

4. Параллельная форма.

Используется много реже и соответствует представлению передаточной функции в виде суммы биквадратных блоков или более простых функций.

Назад

Обращенные формы.

Обращение графов выполняется путем изменения направления всех ветвей цепи, при этом вход и выход графа также меняются местами. Для ряда систем такая транспозиция позволяет реализовать более эффективные алгоритмы обработки данных. Пример обращения графа прямой канонической формы рекурсивной системы (с перестроением на расположение входа с левой стороны) приведен на рис.

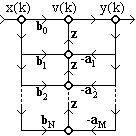
Назад

Понятие многомерного сигнала.

Многомерные сигналы представляют собой функции P независимых переменных при P>1. В общем случае, сигнал может быть непрерывным, дискретным или смешанным.

В общем случае, двумерный непрерывный сигнал представляет собой функцию, значения которой зависят от двух независимых переменных :

s(x,y) = sin(x²+y²), - < x,y <

Двумерный дискретный сигнал (цифровой массив):

s_n,m = s(nx,my), - < n,m <

Назад

Двумерный единичный импульс

(nx,my) = _n,m или единичный отсчет:

_n,m = 1, при n = m = 0.

= 0, при n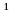 0, m 0.

_n,m = _n _m,

где _n, _m - одномерные единичные импульсы (импульсы Кронекера) по координатам n и m.

Назад

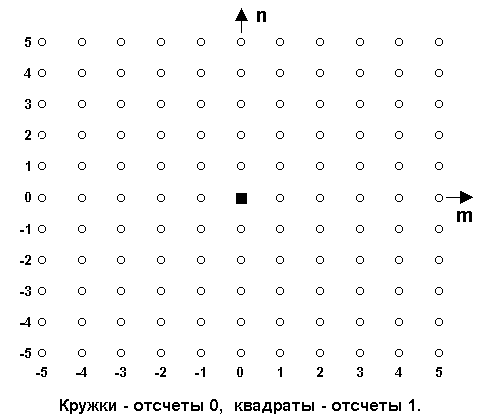
Двумерный линейный импульс

представляет собой последовательность единичных отсчетов по одной координате: s(n,m) = (n) или s(n,m) = (m).

На рис. 11.1.3 приведены два двумерных линейных импульса, первый - по координате m = 0: s(n,m) = (m), и второй импульс по координате n = 2: s(n,m) = (n-2).

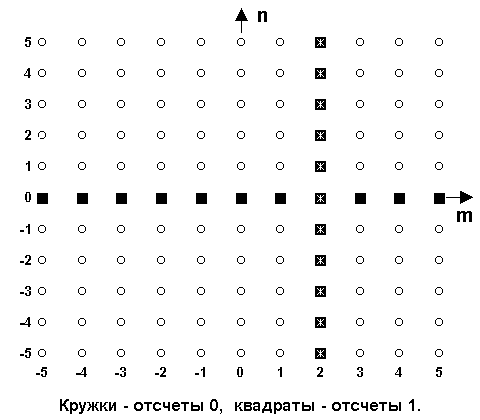
Назад

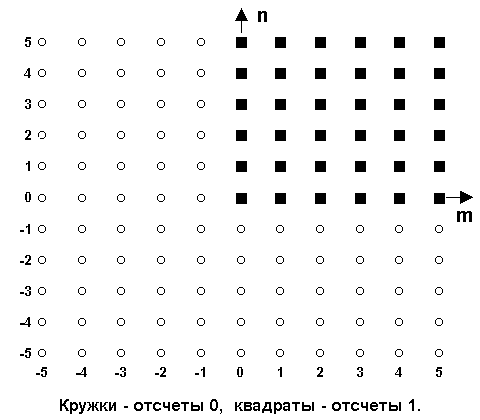
Двумерная единичная ступенька

u(n,m) определяется выражением:

u(n,m) = 1, при n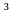 0 и m 0,

= 0, в остальных случаях.

u(n,m) = u(n) u(m),

Назад

Экспоненциальная последовательность:

s(n,m) = exp(jn₁+jm₂)

Назад

Разделимые последовательности.

Разделимой называют последовательность, которую можно представить в виде произведения одномерных последовательностей. Так, для двумерной разделимой последовательности:

s(n,m) = s(n) s(m).

Разделение возможно для немногих практических сигналов. Однако любое двумерное множество с конечным числом ненулевых отсчетов разлагается на конечную сумму разделимых последовательностей:

s(n,m) =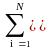 s_in(n) s_im(m),

где N- число ненулевых строк или столбцов массива.

Назад

Конечные последовательности

Важным классом сигналов являются последовательности конечной протяженности, для которых сигнал равен нулю вне определенной области, называемой опорной областью сигнала.

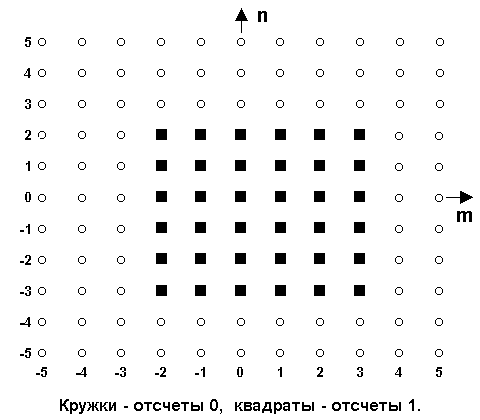
На рис. условно представлена двумерная последовательность конечной протяженности, значения которой отличны от нулевых только внутри ограниченной прямоугольной области -3 n 2, -2 m 3.

Назад

Периодические последовательности.

Двумерные последовательности могут быть периодическими, регулярно повторяющимися в пространстве. Последовательность, удовлетворяющая условиям:

s(n,m+M) = s(n,m),

s(n+N,m) = s(n,m),

обладает периодичностью в двух направлениях, по n и по m. Значения М и N называют интервалами периодичности. Прямоугольная форма области периода (наиболее удобна при обработке данных, но не является единственно возможной.

Общие условия периодичности:

s(n+N₁, m+M₁) = s(n,m),

s(n+N₂, m+M₂) = s(n,m),

D = N₁M₂ - N₂M₁ 0.

Упорядоченные пары (N₁,M₁) и (N₂,M₂) представляют собой смещения от отсчетов одного периода к соответствующим отсчетам других периодов и могут рассматриваться как векторы N и M, которые образуют области периодов в форме параллелограмма.

Назад

Базовыми операциями

в системах, комбинациями которых осуществляются преобразования, являются операции скалярного умножения, сдвига и сложения:

z(n,m) = c s(n,m),

z(n,m) = s(n-N,m-M),

z(n,m) = s(n,m)+u(n,m).

Обобщением скалярного умножения является пространственное маскирование:

z(n,m) = c_n,m s(n,m)

Назад

Линейные системы.

Система считается линейной при выполнении двух условий:

1. Пропорциональное изменение входного сигнала вызывает пропорциональное изменение выходного сигнала.

2. Суммарный сигнал двух входных последовательностей дает суммарный сигнал двух соответствующих выходных последовательностей.

Другими словами, если оператор Т[s(x,y)] описывает линейную систему и имеет место z(x,y) = Т[s(x,y)], q(x,y) = Т[u(x,y)], то Т[as(x,y)+bu(x,y)] = az(x,y)+bq(x,y).

Назад

Инвариантность к сдвигу.

Система инвариантна к сдвигу, если сдвиг входной последовательности приводит к такому же сдвигу выходной последовательности:

Т[s(n-N,m-M)] = z(n-N,m-M).

Линейность и инвариантность к сдвигу являются независимыми свойствами системы.

Назад

Импульсный отклик

на произвольно расположенный входной импульс, как следует из выражения (11.2.3), описывается выражением:

h_ij(n,m) = T[(n-n_i,m-m_j)].

Для частного случая i = j = 0 имеем:

h_o(n,m) = T[(n,m)].

Используя принцип инвариантности к сдвигу, получим:

h_ij(n,m) = h_o(n-i,m-j) = h(n-i,m-j), (11.2.4)

т.e. импульсный отклик на произвольно расположенный входной импульс равен сдвинутому импульсному отклику на входной импульс, расположенный в начале координат.

Назад

Двумерная свертка

z(n,m) = _k _l h(k,l) s(n-k,m-l),

двумерная свертка коммутативна, как и одномерная. бладает свойством ассоциативности (результат не зависит от порядка свертки). Эти свойства определяют и основное свойство двумерных линейных систем при их параллельном и/или последовательном соединении – результирующая система также является линейной.

Для упрощения символьного аппарата двумерную свертку обозначают индексом (_**):

z(n,m) = h(k,l) _** s(n-k,m-l).

Разделимые системы.

Если импульсный отклик системы может быть разделен:

h(k,l) = h(k) h(l), Система с таким откликом называется разделимой.

свертка принимает вид:

z(n,m) = _k h(k) _l h(l) s(n-k,m-l),

Назад

Специальные двумерные системы.

На практике используются также системы с несколькими входами и/или выходами.

Допустим, система имеет i-входы и j-выходы, линейна и инвариантна к сдвигу по переменной t. Если на i-вход системы поступает одномерный единичный импульс _i(t) при нулевых сигналах на остальных входах, то j-выходные сигналы будут импульсным откликом системы h_ij(t). При известном полном ансамбле значений h_ij для всех i-входов, для произвольной комбинации входных сигналов s_i(t) сигнал на j-выходе будет определяться выражением:

z_j(t) = _i _k h_ij(k) s_i(t-k).

Назад

Частотный отклик системы. =

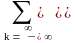
H(_x,_y) = h(k,l) exp(-jk_x-jl_y).

Сигнал представляет собой комплексную синусоиду с теми же значениями частоты, что и у входного сигнала, с изменением амплитуды и фазы за счет комплексного множителя H(_x,_y), который носит название частотного отклика (частотной характеристики) системы.

Назад

Импульсный отклик системы.

Обратным преобразованием Фурье с интегрированием в пределах одного периода из частотного отклика H(_x,_y) можно получить импульсный отклик системы:

h(k,l) = H(_x,_y) exp(jk_x+jl_y) d_xd_y.

Назад

Свойства двумерного преобразования Фурье.

1. Фурье-преобразования сигналов.

S(_x,_y) = _n _m s(n,m) exp(-jn_x-jm_y).

s(n,m) = S(_x,_y) exp(jn_x+jm_y) d_xd_y.

2. Теорема о свертке.

z(n,m) = h(n,m) _** s(n,m)  H(_x,_y) S(_x,_y) = Z(_x,_y).

3. Основные свойства Фурье-преобразования.

1) Линейность:

аs(n,m)+bz(n,m)  aS(_x,_y)+bZ(_x,_y).

2) Пространственный сдвиг:

s(n-N,m-M)  S(_x,_y) exp(-jN_x-jM_y).

4) Комплексное сопряжение:

х*(n,m)  S*(-_x,-_y).

5) Теорема Парсеваля:

_n _m |s(n,m)|² = |S(_x,_y)|² d_x d_y,

где левая часть уравнения представляет собой полную энергию дискретного сигнала s(n,m), a функция |S(_n,_m)|² - спектральную плотность энергии сигнала.

Назад

Прямоугольный растр дискретизации.

Из способов обобщения одномерной периодической дискретизации на двумерный случай наиболее простым является периодическая дискретизация в прямоугольных координатах:

s(n,m) = s_a(nx,my),

где x и y - горизонтальный и вертикальный интервалы дискретизации двумерного непрерывного сигнала s_a(x,y).

Дискретные преобразования Фурье:

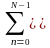
S(k,l) = 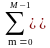s(n,m) exp(-jnk/N-jm2l/M),

S(k,l) = exp(-jn2k/N) s(n,m) exp(-jm2l/M),

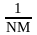
s(n,m) = 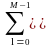S(k,l) exp(-jn2k/N-jm2l/M).

s(n,m) = exp(-jn2k/N) S(k,l) exp(-jm2l/M).

Выражения показывают, что двумерное ДПФ по прямоугольному растру дискретизации данных может вычисляться с помощью одномерных последовательных ДПФ.

Назад

Интерполяционный ряд восстановления двумерного сигнала.

Если непрерывный сигнал s_a(x,y) является сигналом с ограниченным спектром то, как и в одномерном случае, сигнал s_a(x,y) может быть восстановлен по дискретному сигналу с использованием двумерного аналога ряда Котельникова-Шеннона:

s_a(x,y) = _n _m s(n,m) .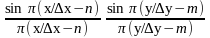

Назад

Произвольный растр дискретизации.

Произвольный растр дискретизации с линейно независимыми векторами 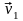= (v₁₁,v₂₁)^T и 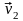= (v₁₂,v₂₂)^T, где T - индекс транспонирования. Координаты двумерного периодического множества отсчетов на плоскости (x,y):

x = v₁₁n + v₁₂m,

y = v₂₁n + v₂₂m.

С использованием векторных обозначений:

,

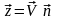где 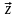= (x,y)^T, 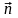=(n,m)^T, 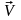=( | )- матрица дискретизации. При дискретизации непрерывного сигнала s_a(x,y) матрицей формируется дискретный сигнал:

s( )  s_a( ).

Назад

Двумерное интегральное преобразование Фурье

непрерывного сигнала по непрерывному вектору 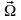= (₁,₂)^T:

S_a( ) = s_a( ) exp(-j ^T ) d , (11.4.6)

s_a( ) = S_a( ) exp(j ^T ) d , (11.4.7)

Данные интегралы являются двойными, поскольку дифференциалы d и d являются векторами.

Назад

Преобразование Фурье дискретного сигнала:

S(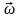 ) = _n s( ) exp(-j ^T ),

s( ) = S( ) exp(j ^T ) d .

где: = (_х,_у)^T .

Выражение s( ) может быть получено дискретизацией выражения s_a( )

s( ) = s_a( ) = S_a( ) exp(j ^T ) d .

После подстановки в это выражение значения = ^T, получаем:

s( ) = 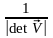S_a( / ^T) exp(j ^Т ) d .

В случае прямоугольной дискретизации:

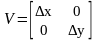, det = ху,

Назад

Интерполяция дискретных сигналов.

Уравнение восстановления непрерывной функции по ее дискретному варианту (многомерный аналог интерполяционного ряда Котельникова-Шеннона):

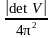
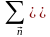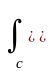s_a( ) = s( ) exp(j ^T ( - )) d .

s_a( ) = s( ) f( - ), (11.4.17)

где f(..) – интерполяционная функция:

f( - ) = exp(j ^T ( - )) d .

Назад

Прямоугольный и гексагональный растры дискретизации.

На практике для двумерных сигналов используют, как правило, только два варианта растров дискретизации - прямоугольный и гексагональный.

Прямоугольному варианту соответствуют диагональные матрицы дискретизации и периодичности

, det = ху

.

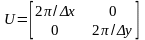Для гексагональной дискретизации, в частном случае при t = х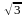 каждый отсчет располагается на равном расстоянии от шести ближайших отсчетов, при этом матрицы дискретизации:

, .

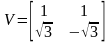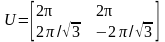Допустим, имеем сигнал с частотным спектром, ограниченным круговой областью частот _r:

S_a(_х,_у) = 0 при _х²+_у² > _r².

Круговая область частот вписывается без перекрытий в квадрат со стороной 2_r или в шестиугольник со стороной 2_r/ . Матрицы дискретизации:

_пр = , det = ²/_r²,

_гекс =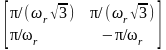 , det = 2²/(_r² ).

Поскольку плотность отсчетов пропорциональна 1/|det |, то отсюда следует, что для представления одного и того же сигнала гексагональный растр дискретизации требует на 13.4% меньше отсчетов по сравнению с прямоугольным. Эффективность "гексагональной" матрицы возрастает при увеличении размерности сигнала. Так, при 4-мерном сигнале для "гексагональной" матрицы требуется в 2 раза меньше отсчетов, чем для "прямоугольной".

Назад

Периодические последовательности.

Двумерная последовательность s(n,m) прямоугольно периодична, если

s_п(n,m) = s(n,n+M) = s(n+N,m)

для всех (n,m) при целочисленных значениях N и M. Минимальные значения N и M, при которых выполняется данное равенство, называют горизонтальным и вертикальным периодами функции s_п(..), которыми ограничивается прямоугольная область R_N,M главного периода, содержащая NM независимых отсчетов: 0 n N-1, 0 m M-1.

Последовательность s_п(n,m) с периодами N и M можно представить в виде конечной суммы (ряда Фурье) комплексных синусоид с кратными частотами:

s_п(n,m) =(1/NM) S_п(k,l) exp(j2nk/N+j2ml/M).

S_п(k,l) =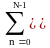 s_п(n,m) exp(-j2nk/N-j2ml/M).

Назад

Конечные последовательности.

Если s(n,m) представляет собой последовательность конечной протяженности, имеющей опорную область R_N,M, то периодическую последовательность s_п(n,m) с главным периодом R_N,M можно сформировать периодическим продолжением s(n,m):

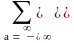
s_п(n,m) = s(n-aN,m-bM),

s(n, m) = s_п(n, m), (n, m) < R_N,M.

= 0, в остальных случаях.

Отсюда следует, что любой финитный сигнал может быть полностью определен своим периодическим продолжением и опорной областью.

Назад

Случайный процесс Х(t)

представляет собой функцию, которая отличается тем, что принимаемые ею значения в любые произвольные моменты времени по координате t являются случайными. Строго с теоретических позиций, случайный процесс X(t) следует рассматривать как совокупность временных функций x_k(t), имеющих определенную общую статистическую закономерность. При регистрации случайного процесса на определенном временном интервале осуществляется фиксирование единичной реализации x_k(t) из бесчисленного числа возможных реализаций процесса X(t). Эта единичная реализация называется выборочной функцией случайного процесса Сам случайный процесс в целом должен анализироваться с позиции бесконечной совокупности таких реализаций, образующих статистический ансамбль. Полной статистической характеристикой такой системы является N-мерная плотность вероятностей р(x_n;t_n).

Назад

Одномерная функция распределения вероятностей

(x,t_i) определяет вероятность того, что в момент времени t_i значение случайной величины X(t_i) не превысит значения x:

F(x,t_i) = P{X(t_i)≤x}.

P{a<X(t_i)≤b} = F(b,t_i) – F(a,t_i).

Назад

Одномерная плотность вероятностей

p(x,t) случайного процесса Х(t) характеризует распределение вероятностей реализации случайной величины Х(t_i) в произвольный момент времени t_i. Она представляет собой производную от функции распределения вероятностей:

p(x,t_i) = dF(x,t_i)/dx.

При известной функции плотности вероятностей вероятность реализации значения X(t_i) в произвольном интервале значений [a, b] вычисляется по формуле:

P(a<X(t_i)≤b) =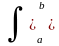 p(x,t_i) dx.

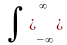p(x,t_i) dx =1.

Назад

Математическое ожидание

(mean value) представляет собой статистическое усреднение случайной величины X(t_i). Соответственно, функция математического ожидания является теоретической оценкой среднего значения случайного процесса по временной оси:

m_x(t)  M{Х(t)}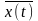 = x p(x;t) dx,

Математическое ожидание m_x(t) представляет собой неслучайную составляющую случайного процесса X(t).

Назад

Функция дисперсии

(variance) случайного процесса является теоретической оценкой среднего значения разности Х(t)-m_x(t), которая называется флюктуационной частью процесса:

D_x(t) = M{[Х(t)-m_x(t)]²} = M{X²(t)} - m_x²(t) = [ x(t)-m_x(t)]² p(x;t) dx

Назад

Функция среднего квадратического отклонения

(standard deviation) служит амплитудной мерой разброса значений случайного процесса по временной оси относительно математического ожидания процесса:

_x(t)= .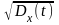

Учитывая последнее выражение, дисперсия случайной величины обычно обозначается индексом _x².

Назад

Корреляционные функции случайных процессов.

Двумерная плотность вероятностей p(x₁,x₂; t₁,t₂) определяет вероятность совместной реализации значений случайных величин Х(t₁) и Х(t₂) в произвольные моменты времени t₁ и t₂ и в какой-то мере уже позволяет оценивать динамику развития процесса.

Характеристикой динамики изменения двумерной случайной величины {X(t_i), X(t_j)} является корреляционная функция, которая описывает случайный процесс в целом:

R_X(t_i,t_j) = M{X(t₁) X(t₂)}.

По всему пространству значений случайного процесса X(t) корреляционная функция определяется выражением:

R_x(t_i,t_j) = x(t_i)x(t_j) p(x_i,t_j; x_i,t_j) dx_i dx_j

Назад

Автокорреляционная функция случайного процесса.

При анализе случайных процессов второй момент времени t_j удобно задавать величиной сдвига  относительно первого момента, который при этом может быть задан в виде координатной переменной:

R_Х(t,t+) = M{Х(t)Х(t+)}.

Назад

Ковариационная функция.

Представляет собой статистически усредненное произведение значений центрированной случайной функции X(t)-m_x(t) в моменты времени t_i и t_j и характеризует флюктуационную составляющую процесса:

K_Х(t_i,t_j) = (x(t_i)-m_x(t_i)) (x(t_j)-m_x(t_j)) p(x_i,t_j; x_i,t_j) dx_i dx_j

Назад

Свойства функций автоковариации и автокорреляции.

1. Максимум функций наблюдается при = 0. Это очевидно, т.к. при = 0 вычисляется степень связи отсчетов с собой же, которая не может быть меньше связи разных отсчетов.

2. Функции автокорреляции и автоковариации являются четными: R_X() = R_X(-).. Говоря иначе, моменты двух случайных величин X(t₁) и X(t₂) не зависят от последовательности, в которой эти величины рассматриваются.

3. При значения ФАК для сигналов, конечных по энергии, стремятся к нулю, что прямо следует из физического смысла ФАК. Это позволяет ограничивать длину ФАК определенным максимальным значением _max - радиусом корреляции, за пределами которого отсчеты можно считать независимыми.

4. Если к случайной функции X(t) прибавить неслучайную функцию f(t), то ковариационная функция не изменяется.

5. Если случайную функцию X(t) умножить на неслучайную функцию f(t), то ее корреляционная функция R_x(t₁,t₂) умножится на f(t₁)f(t₂).

6. При умножении функции случайного процесса на постоянное значение С значения ФАК увеличиваются в С² раз.

Назад

Взаимные моменты случайных процессов

дают возможность оценить совместные свойства двух случайных процессов X(t) и Y(t). Мера связи между двумя случайными процессами X(t) и Y(t) также устанавливается корреляционными функциями, а именно - функциями взаимной корреляции и взаимной ковариации. В общем случае, для произвольных фиксированных моментов времени t₁ = t и t₂ = t+:

R_XY(t,t+) = M{X(t)Y(t+)}.

K_XY(t,t+) = M{(X(t)-m_x(t))(Y(t+)-m_y(t+))}.

Взаимные функции являются произвольными функциями (не обладают свойствами четности или нечетности), и удовлетворяют следующим соотношениям:

R_xy(-) = R_yx(),

|R_xy()|²  R_x(0)R_y(0).

Назад

Статистическая независимость случайных процессов

определяет отсутствие связи между значениями двух случайных величин X и Y. Это означает, что плотность вероятности одной случайной величины не зависит от того, какие значения принимает вторая случайная величина. Двумерная плотность вероятностей при этом должна представлять собой произведения одномерных плотностей вероятностей этих двух величин:

p(x,y) = p(x) p(y).

Это условие является обязательным условием статистической независимости случайных величин. В противном случае между случайными величинами может существовать определенная статистическая связь. Как линейная, так и нелинейная. Мерой линейной статистической связи является коэффициент корреляции:

r_xy = [M{X·Y} – M{X)·M{Y}]/ .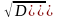

Значений r_xy могут изменяться в пределах от -1 до +1. В частном случае, если случайные величины связаны линейным соотношением x=ay+b, коэффициент корреляции равен ±1 в зависимости от знака константы а. Случайные величины некоррелированны при r_xy=0, при этом из выражения для r_xy следует:

M{X·Y} = M{X}·M{Y}.

Из статистической независимости величин следует их некоррелированность. Обратное не очевидно. Так, например, случайные величины x=cos  и y=sin , где  - случайная величина с равномерным распределением в интервале 0…2, имеют нулевой коэффициент корреляции, и вместе с тем их зависимость очевидна.

Назад

Нестационарные процессы.

В общем случае значения функций математического ожидания, дисперсии и корреляции могут быть зависимыми от момента времени t, т.е. изменяться во времени. Такие процессы составляют класс нестационарных процессов.

Назад

Стационарные процессы.

Процесс называют стационарным, если плотность вероятностей процесса не зависит от начала отсчета времени и если на интервале его существования выполняются условия постоянства математического ожидания и дисперсии, а корреляционная функция является функцией только разности аргументов = t₂-t₁, т.e.:

Т.е. случайная функция считается стационарной, если ее математическое ожидание постоянно, а корреляционная функция зависит только от одного аргумента. Случайные процессы, удовлетворяющие условиям стационарности на ограниченных, интересующих нас интервалах, также обычно относят к числу стационарных в широком смысле и называют квазистационарными.

Назад

Эргодические процессы.

Закон распределения случайных величин в таком процессе может быть одним и тем же как по сечению для ансамбля реализаций, так и по координате развития. Такие процессы получили название эргодических (ergodic).

Для эргодических процессов имеет место:

m_X(t) = M{x(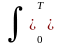t)} = x(t) dt,

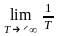
D_Х(t) = M{[x(t) - m_Х(t)]²} = (x(t) - m_Х(t))² dt

R_Х() = M{x(t)x(t+)} = x(t)x(t+) dt

Эргодичность является очень важным свойством случайных стационарных, и только стационарных процессов. Математическое ожидание случайного эргодического процесса равно постоянной составляющей любой его реализации

Практическая проверка эргодичности процесса обычно производится проверкой выполнения условия Слуцкого:

K() d = 0

Если ковариационная функция процесса стремится к нулю при возрастании значения аргумента (), то процесс относится к числу эргодических, по крайней мере, относительно моментов первого и второго порядков.

Назад

Каноническое разложение случайных функций.

Произвольная нецентрированная случайная функция соответственно может быть представлена в виде

X(t) = m_x(t) + ⁰X(t) = m_x(t) +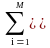 X_i_i(t),

где ⁰X(t) - флюктуационная составляющая случайной функции X(t). Выражение и является каноническим разложением функции X(t). Случайные величины X_i называются коэффициентами разложения, функции _i - координатными функциями разложения.

Назад

Комплексные случайные функции.

В общем случае случайный процесс может описываться комплексной случайной функцией:

Z(t) = X(t) + jY(t),

где X(t) и Y(t) - действительные случайные функции. Соответственно, математическое ожидание комплексной функции:

m_z(t) = m_x(t)+jm_y(t).

Выражение для вычисления корреляционной функции имеет следующий вид:

R_z(t₁,t₂) = M{Z(t₁)Z*(t₂)}= M{[X(t₁)+jY(t₁)][X(t₂)-jY(t₂)]}=

= R_x(t₁,t₂) + R_y(t₁,t₂) + j[R_yx(t₁,t₂) - R_xy(t₁,t₂)].

Назад

Финитное преобразование Фурье

Отдельно взятая на интервале 0-Т реализация x_k(t) стационарного случайного процесса ⁰X(t) может быть представлена в виде ряда Фурье:

x_k(t) =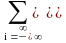 V_x,k(_i) exp(j_it) 

V_x,k(_i)= (1/T) x_k(t) exp(-j_it) dt

Под спектрами случайных процессов понимается не преобразования Фурье случайных функций, а преобразования Фурье функций мощности случайных процессов.

Назад

Спектры мощности случайных функций

Средняя мощность случайного процесса X(t), зарегистрированного в процессе одной реализации на интервале 0-Т вычислена по формуле:

P_T = [x²(t)/T] dt = [|X_T(f)|²/T] df,

где X(f) – спектральная плотность единичной реализации x(t).

Спектральная плотность средней мощности данной реализации случайного процесса:

W(f) = |X_T(f)|².

Средняя мощность любой реализации центрированного процесса равна его дисперсии:

D_x = W(f) df.

Назад

Спектр функций случайных процессов.

При представлении ковариационной функции на интервале 0-Т, шаг по спектру функции с учетом четности ковариационной функции устанавливаетсяравным  = /T, _i = i, а спектр определяется обычно непосредственно по косинусам в односторонней форме:

K_x() = D_x(_i) exp(j_i)

D_x(_i) = (2/T) K_x() exp(-j_i) d,

где D_x(_i) - дисперсии случайных величин

Дисперсия стационарного случайного процесса X(t) может определяться по формуле при  = 0:

D_x= D_x(_i),

т.е. дисперсия стационарного случайного процесса равна сумме дисперсий всех случайных гармоник ее спектрального разложения.

Обобщенной характеристикой спектра случайного процесса служит эффективная ширина спектра, определяемая по формуле:

B_k = (/D_max D_x(_i) = D_x/D_max,

где D_maxмаксимальное значение функции D_x(_i).

Назад

Соотношение неопределенности

связывает эффективную ширину спектра B_k с эффективным интервалом ковариации T_k. Для его определения найдем произведение B_kT_k случайного процесса

B_kT_k=2 |K_x()|d/S_x(f)_max

Оценка этого произведения и приводит к соотношению неопределенности:

B_kT_k1/2. Следовательно, с уменьшением эффективной ширины спектра увеличивается эффективный интервал ковариации случайного процесса, и наоборот.

Назад

Взаимные спектральные функции.

Функции взаимного спектра представляют собой комплексные выражения:

S_xy(_i)=(1/T)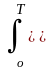 K_xy()exp(-j_i)d,

при этом:

S_xy(-) = S_xy^*() = S_yx().

Функция когерентности определяется выражением:

_xy²() = |S_xy()|²/(S_x()S_y()),

и для любых  удовлетворяет неравенствам

0  _xy²()  1.

Функция когерентности обычно используется при анализе линейных систем преобразования входной функции X(t) в выходную функцию Y(t) (рассмотрено ниже).

Назад

Теорема Винера-Хинчина.

Корреляционная функция случайного стационарного эргодического процесса представляет собой обратное преобразование Фурье его спектра мощности, и наоборот:

W() = R() exp(-j) d.

Так как ковариационные функции стационарных процессов являются частным случаем корреляционных функций, то эти выражения действительны и для ФАК, а, следовательно, спектральные функции случайных процессов, рассмотренные выше как преобразования Фурье ковариационных функций, являются спектрами мощности флюктуирующей составляющей процессов. С этих позиций дисперсия случайных процессов представляет собой среднюю мощность его флюктуаций

K() = ² = (1/2) W() d

т.е. равна суммарной мощности всех его частотных составляющих процессов.

Назад