
Оглавление
Общие понятия систем. 2
Линейные системы. 3
Основные системные операции. 3
Инвариантность систем к сдвигу. 3
Математическая модель системы задается связью между сигналами входа и выхода 4
Нерекурсивные цифровые системы. 4
Рекурсивные цифровые системы. Системы, которые описываются полным разностным уравнением 4
Стационарные и нестационарные системы. 5
Импульсный отклик системы. 5
Реакция системы на произвольный сигнал. 5
Усиление постоянной составляющей сигнала. 5
Усиление шумов. 6
Определение импульсной реакции 6
Передаточные функции систем 6
Структурные схемы. 7
Графы систем. 7
Соединения систем. 7
1. Последовательное соединение. 7
2. Параллельное соединение. 8
3. Соединение обратной связи. 8
Схемы реализации систем. 8
1. Прямая форма. 8
2. Прямая каноническая форма 8
3. Каскадная (последовательная) форма. 9
4. Параллельная форма. 9
Обращенные формы. 9
Понятие многомерного сигнала. 9
Двумерный единичный импульс 10
Двумерный линейный импульс 10
Двумерная единичная ступенька 10
Экспоненциальная последовательность: 11
Разделимые последовательности. 11
Конечные последовательности 11
Периодические последовательности. 11
Базовыми операциями 12
Линейные системы. 12
Инвариантность к сдвигу. 12
Импульсный отклик 12
Двумерная свертка 13
Разделимые системы. 13
Специальные двумерные системы. 13
Частотный отклик системы. = 13
Импульсный отклик системы. 13
Свойства двумерного преобразования Фурье. 14
Прямоугольный растр дискретизации. 14
Интерполяционный ряд восстановления двумерного сигнала. 15
Произвольный растр дискретизации. 15
Двумерное интегральное преобразование Фурье 15
Преобразование Фурье дискретного сигнала: 15
Интерполяция дискретных сигналов. 16
Прямоугольный и гексагональный растры дискретизации. 16
Периодические последовательности. 17
Конечные последовательности. 17
Случайный процесс Х(t) 18
Одномерная функция распределения вероятностей 18
Одномерная плотность вероятностей 18
Математическое ожидание 18
Функция дисперсии 19
Функция среднего квадратического отклонения 19
Корреляционные функции случайных процессов. 19
Автокорреляционная функция случайного процесса. 19
Ковариационная функция. 20
Свойства функций автоковариации и автокорреляции. 20
Взаимные моменты случайных процессов 20
Статистическая независимость случайных процессов 20
Нестационарные процессы. 21
Стационарные процессы. 21
Эргодические процессы. 21
Каноническое разложение случайных функций. 22
Комплексные случайные функции. 22
Финитное преобразование Фурье 22
Спектры мощности случайных функций 23
Спектр функций случайных процессов. 23
Соотношение неопределенности 23
Взаимные спектральные функции. 24
Теорема Винера-Хинчина. 24
Общие понятия систем.
Безотносительно к назначению и исполнению система всегда имеет вход, на который подается входной сигнал или входное воздействие, в общем случае многомерное, и выход, с которого снимается обработанный выходной сигнал. Если устройство системы и внутренние операции преобразований принципиального значения не имеют, то система в целом может восприниматься как “черный ящик”, в формализованном виде. Формализованная система представляет собой определенный системный оператор (алгоритм) преобразования входного сигнала – воздействия s(t), в сигнал на выходе системы y(t) – отклик или выходную реакцию системы. Символическое обозначение операции преобразования (трансформации):
y(t) = T[s(t)].
Системный оператор T - это правило (набор правил, алгоритм) преобразования сигнала s(t) в сигнал y(t).
Совокупность системного оператора Т и пространства сигналов образует математическую модель системы.
Назад
Линейные системы.
Любые преобразования сигналов сопровождаются изменением их спектра и по характеру этих изменений разделяются на два вида: линейные и нелинейные. К нелинейным относят изменения, при которых в составе спектра сигналов появляются новые гармонические составляющие. При линейных изменениях сигналов изменяются амплитуды и/или начальные фазы гармонических составляющих спектра. Оба вида изменений могут происходить как с сохранением полезной информации, так и с ее искажением.
Система считается линейной, если в пределах установленной области входных и выходных сигналов ее реакция на входные сигналы аддитивна (выполняется принцип суперпозиции сигналов) и однородна (выполняется принцип пропорционального подобия).
Назад
Основные системные операции.
К базовым линейным операциям, из которых могут быть сформированы любые линейные операторы преобразования, относятся операции скалярного умножения, сдвига и сложения сигналов:
y(t) = b x(t),
y(t) = x(t-t),
y(t) = a(t)+b(t).
Для систем, с размерностью 2 и более существует также еще одна базовая операция, которая называется операцией пространственного маскирования, которая может рассматриваться как обобщение скалярного умножения. Так, для двумерных систем:
z(x,y) = c(x,y)u(x,y),
где u(x,y) – двумерный входной сигнал, c(x,y) – пространственная маска постоянных (весовых) коэффициентов.
Назад
Инвариантность систем к сдвигу.
Система называется инвариантной к сдвигу, если сдвиг входного сигнала по аргументам вызывает соответствующий сдвиг выходного сигнала:
s(x,t) = T[a(x,t)], T[a(x-x,t-t)] = s(x-x,t-t).
В теории анализа и обработки данных основное место занимают системы, линейные и инвариантные к сдвигу (ЛИС - системы).
Преимущество, которое отдается ЛИС - системам в методах обработки информации, базируется на возможности разложения входного сигнала любой, сколь угодно сложной формы, на составляющие простейших форм, отклик системы на которые известен и хорошо изучен, с последующим вычислением выходного сигнала в виде суммы откликов на все составляющие входного сигнала.
Другой важной особенностью ЛИС - систем является то, что любые их комбинации также являются ЛИС – системой, при этом, по отношению к общей системной операции преобразования, порядок соединения входящих в нее систем значения не имеет.
Назад
Математическая модель системы задается связью между сигналами входа и выхода
y(kt)
=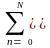 bn
s((k-n)t)
-
bn
s((k-n)t)
-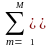 am
y((k-m)t).
am
y((k-m)t).
Назад
Нерекурсивные цифровые системы.
При нулевых значениях коэффициентов am
y(kt) = bn s((k-n)t) - am y((k-m)t).
уравнение (9.1.2') переходит в уравнение дискретной свертки x(k) с оператором bn:
y(k) = bn x(k-n).
При установленных значениях коэффициентов bn значения выходных отсчетов свертки для любого аргумента k определяются текущим и "прошлыми" значениями входных отсчетов. Такая система называется нерекурсивной цифровой системой (НЦС).
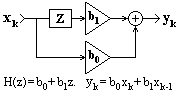
Назад
Рекурсивные цифровые системы. Системы, которые описываются полным разностным уравнением
y(kt) = bn s((k-n)t) - am y((k-m)t).
, принято называть рекурсивными цифровыми системами (РЦС) или рекурсивными цифровыми фильтрами (РЦФ), так как в вычислении текущих значений выходного сигнала участвует не только входной сигнал, но и значения выходного сигнала, вычисленные в предшествующих циклах расчетов. С учетом последнего фактора рекурсивные системы называют системами с обратной связью.
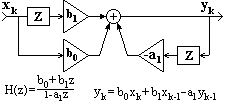
Назад
Стационарные и нестационарные системы.
Система считается стационарной и имеет постоянные параметры, если ее свойства (математический алгоритм оператора преобразования) в пределах заданной точности не зависят от входного и выходного сигналов и не изменяются ни во времени, ни от каких-либо других внешних факторов.
В противном случае система является нестационарной или параметрической (системой с переменными параметрами). Среди последних большое значение имеют так называемые адаптивные системы обработки данных. В этих системах производится, например, оценивание определенных параметров входных и выходных сигналов, по результатам сравнения которых осуществляется подстройка параметров преобразования (переходной характеристики системы) таким образом, чтобы обеспечить оптимальные по производительности условия обработки сигналов или минимизировать погрешность обработки.
Назад
Импульсный отклик системы.
По определению, импульсными характеристиками систем называются функции h(kt) для цифровых систем, которые является реакцией (откликом) систем на единичные входные сигналы: импульс Кронекера (kt) для цифровых систем, поступающие на вход систем соответственно при k=0. Эта реакция однозначно определяется оператором преобразования:
y(kt) = T[(kt)] h(kt).
Под временем (длиной) реакции системы обычно понимают интервал, на котором значения функции h(t) существенно отличаются от нуля после прекращения действия единичного сигнала на ее входе.
Назад
Реакция системы на произвольный сигнал.
Если функция импульсного отклика системы известна, то произвольный сигнал на входе системы может быть разложен в линейную последовательность взвешенных единичных импульсов:
y(t) =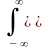 s()
Т[(t-)]
d
s()
Т[(t-)]
d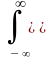 s()
h(t-)
d
s()
h(t-)
d
Это выражение представляет собой свертку входного сигнала с импульсной характеристикой системы.
Назад
Усиление постоянной составляющей сигнала.
Подадим на вход системы постоянный сигнал s(t) = A. При этом сигнал на выходе системы:
y(t) = h() s(t-) d = А h() dАКпс,
т.е. площадь импульсного является коэффициентом Кпс усиления постоянной составляющей входного сигнала.
Если при обработке сигналов должны изменяться только динамические характеристики их формы без изменения постоянной составляющей, то площадь импульсного отклика должна нормироваться к единице.
Назад
Усиление шумов.
Допустим, что
система имеет нормированный к 1 импульсный
отклик h(k). Обозначим через (k)
аддитивный шум с математическим ожиданием
M{(k)}=
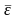 = 0 и дисперсией D2,
который в сумме с сигналом поступает
на вход системы. Значения (k)
статистически независимы и некоррелированы
с сигналом. С учетом помехи во входном
сигнале значение сигнала на выходе
системы:
= 0 и дисперсией D2,
который в сумме с сигналом поступает
на вход системы. Значения (k)
статистически независимы и некоррелированы
с сигналом. С учетом помехи во входном
сигнале значение сигнала на выходе
системы:
y(k)
=
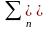 h(n)[x(k-n)+(k-n)].
h(n)[x(k-n)+(k-n)].
Математическое ожидание значений выходного сигнала:
M{y(k)} = h(n)[x(k-n)+M{(k-n)}] = h(n) x(k-n).
Если правую часть последнего выражения представить в виде
M{[
h(n)
(k-n)][ h(m) (k-m)]},
h(m) (k-m)]},
то в этом выражении математические ожидания всех членов произведения с сомножителями (n)(m) при n m равны 0 в силу статистической независимости значений шума. Остаются только члены с n = m, т.е.:
M{ h2(n)2(n)} = h2(n) M{2(n)} = D h2(n) = 2 h2(n).
Отсюда следует, что сумма квадратов значений нормированного импульсного отклика системы представляет собой коэффициент усиления аддитивных шумов во входном сигнале.
Назад
Определение импульсной реакции
требуется, как правило, для рекурсивных систем, так как импульсная реакция для НЦС специального определения не требует:
h(k)
=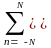 b(n)(k-n)
b(k).
b(n)(k-n)
b(k).
Если выражение для системы известно в общей форме
y(kt) = bn s((k-n)t) - am y((k-m)t).
, определение импульсной реакции производится подстановкой в уравнение системы импульса Кронекера с координатой k = 0 при нулевых начальных условиях, при этом сигнал на выходе системы будет представлять собой импульсную реакцию системы: y(k) h(k).
Пример. Уравнение РЦС: yk = xk + 0.5yk-1. Входной сигнал: xk= o= {1,0,0,0,...}.
Расчет выходного сигнала при нулевых начальных условиях:
yo = xo+0.5 y-1 = 1+0 = 1 = ho. y1 = x1+0.5 yo = 0+0.5 = 0.5 = h1. y2 = x2+0.5 y1 = 0+0.25 = 0.25= h2
y3 = x3+0.5 y2 = 0.125 = h3. y4 = x4+0.5 y3 = 0.0625 = h4, т.д.
Импульсный отклик системы: hk = {1, 0.5, 0.25, 0.125, ... }
Назад
Передаточные функции систем
Применяя z-преобразование к обеим частям равенства получаем:
Y(z)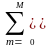 amzm
= X(z)
bnzn,
amzm
= X(z)
bnzn,
где X(z),Y(z)- соответствующие z-образы входного и выходного сигнала. Из этого выражения, полагая ao = 1, получаем в общей форме функцию связи входа и выхода системы - уравнение передаточной функции системы (или системной функции) в z-области:
H(z) = Y(z)/X(z)
=
bnzn (1+
amzm).
(1+
amzm).
Для нерекурсивных систем при am = 0:
H(z) = bnzn.
При подаче на вход системы единичного импульса Кронекера о, имеющего z-образ (z) = zn = 1, сигнал на выходе системы будет представлять собой импульсную реакцию системы y(k) = h(k), при этом:
H(z)
Y(z) = Y(z)/(z) = TZ[y(k)]
=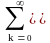 h(k)zk,
(9.3.4)
h(k)zk,
(9.3.4)
т.е. передаточная функция системы является z-образом ее импульсной реакции. При обратном z-преобразовании передаточной функции соответственно получаем импульсную характеристику системы:
h(k) H(z).
Назад
Структурные схемы.
Алгоритмы обработки сигналов в системах наглядно отображаются в виде структурных схем.
Назад
Графы систем.
Наряду со структурной схемой система может быть представлена в виде графа, который отображает диаграмму прохождения сигналов и состоит из направленных ветвей и узлов.
Пример структурной схемы системы с передаточной функцией H(z) = (1+b1z)/(1+a1z) и графа, ей соответствующего
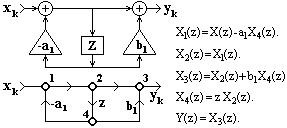
С каждым i узлом графа связано значение сигнала xi(k) или его образа Xi(z), которые определяются суммой всех сигналов или их z-образов входящих в узел ветвей. В каждой ij - ветви (из узла i в узел j) происходит преобразование сигнала в соответствии с передаточной функцией ветви.
Назад
Соединения систем.
