- •В зависимости от областей использования многозадачные ос подразделяются на три типа:
- •Классификация вредоносного по
- •Термин топология сети характеризует способ организации физических связей компьютеров и других сетевых компонентов.
- •Протокол - это набор правил, определяющих взаимодействие абонентов сети и описывающих способ выполнения определённого класса функций.
- •Требования к БнД:
- •Классификация баз данных организации хранения данных и обращения к ним.
- •По типу хранимой информации бд делятся на документальные, фактографические и лексикографические. Среди документальных баз различают библиографические, реферативные и полнотекстовые.
- •Алгоритм - это последовательность инструкций для выполнения какого либо задания.
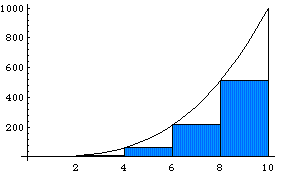
- •Метод трапеций
- •Информационная система — это взаимосвязанная совокупность средств, методов и персонала, используемых для хранения, обработки и выдачи информации для достижения цели управления.
Классификация баз данных организации хранения данных и обращения к ним.
локальные (персональные),
сетевые (интегрированные),
распределенные базы данных.
Персональная база данных - это база данных, предназначенная для локального использования одним пользователем. Локальные БД могут создаваться каждым пользователем самостоятельно, а могут извлекаться из общей БД.
Интегрированные и распределенные БД предполагают возможность одновременного обращения нескольких пользователей к одной и той же информации (многопользовательский, параллельный режим доступа). Это привносит специфические проблемы при их проектировании и в процессе эксплуатации БнД. Распределенные БД, кроме того, имеют характерные особенности, связанные с тем, что физически разные части БД могут быть расположены на разных ЭВМ, а логически, с точки зрения пользователя, они должны представлять собой единое целое.
По типу хранимой информации бд делятся на документальные, фактографические и лексикографические. Среди документальных баз различают библиографические, реферативные и полнотекстовые.
К лексикографическим базам данных относятся различные словари (классификаторы, многоязычные словари, словари основ слов и т. п.).
В системах фактографического типа в БД хранится информация об интересующих пользователя объектах предметной области в виде «фактов» (например, биографические данные о сотрудниках, данные о выпуске продукции производителями и т.п.); в ответ на запрос пользователя выдается требуемая информация об интересующем его объекте (объектах) или сообщение о том, что искомая информация отсутствует в БД.
В документальных БД единицей хранения является какой-либо документ (например, текст закона или статьи), и пользователю в ответ на его запрос выдается либо ссылка на документ, либо сам документ, в котором он может найти интересующую его информацию.
Алгоритм - это последовательность инструкций для выполнения какого либо задания.
Свойства алгоритма:
ДИСКРЕТНОСТЬ – разделение выполнения решения задачи на отдельные операции
ОПРЕДЕЛЕННОСТЬ (точность) алгоритма – определение однозначных действий исполнителя
ПОНЯТНОСТЬ – не должен быть рассчитан на принятие каких-либо самостоятельных решений
Массовость - свойство, когда по данному алгоритму должна решаться не одна, а целый класс подобных задач.
РЕЗУЛЬТАТИВНОСТЬ (конечность) алгоритма – исполнение алгоритма должно закончиться за конечное число шагов
ФОРМЫ ЗАПИСИ АЛГОРИТМОВ:
ЗАПИСАН НА ЕСТЕСТВЕННОМ ЯЗЫКЕ; Алгоритм записывается в виде пронумерованных этапов его выполнения.
ИЗОБРАЖЕН В ВИДЕ БЛОК СХЕМЫ; Алгоритм записывается в виде схемы, состоящей из блоков (геометрических фигур) с размещенными в них действиями. Блоки соединяются стрелочками и показывают структуру всего алгоритма. Алгоритм в виде блок-схемы начинается блоком «начало» и заканчивается блоком «конец».
ЗАПИСАН НА АЛГОРИТМИЧЕСКОМ ЯЗЫКЕ. Это запись алгоритма на специальном языке (в том числе и на языке программирования). Она осуществляется, строго следуя правилам того или иного алгоритмического языка. Заголовок включает в себя название алгоритма, имена исходных данных ( это величины, без которых выполнить алгоритм невозможно) и имена результатов ( это величины, значения которых вычисляются в алгоритме). Для указания начала и конца алгоритма используются служебные слова нач и кон. Между ними записывают одну или несколько команд алгоритма, их называют тело алгоритма.
Производительность алгоритмов:
скорость выполнения двух или более алгоритмов, которые разработаны для выполнения одной и той же задачи.
внутреннюю структуру алгоритма, анализируя его разработку, включая количество тестов сравнения итераций и операторов присваивания, используемых алгоритмом.
Требования к ПК
Размер оперативной памяти
Скорость работы диска
Скорость (частота) работы процессора
Рекурсивные алгоритмы - алгоритмы, вызывающие сами себя до тех пор, пока не будет достигнуто некоторое условие возвращения. Рекурсивными процедурами (recursive procedure) называются процедуры, вызывающие сами себя. Во многих рекурсивных алгоритмах именно степень вложенности рекурсии определяет сложность алгоритма, при этом порядок сложности не всегда легко оценить. Рекурсивная процедура может выглядеть простой, но в то же время серьезно усложнять программу, многократно вызывая саму себя. Но у такого алгоритма есть один существенный минус – он требует огромных машинных ресурсов. Посудите сами, необходимо хранить в памяти для каждой "копии" функции все те данные, которыми вы пользовались, не говоря уже о самой функции.
По цели использования модели классифицируются на научный эксперимент, в котором осуществляется исследование модели с применением различных средств получения данных об объекте, возможности влияния на ход процесса, с целью получения новых данных об объекте или явлении; комплексные испытания и производственный эксперимент, использующие натурное испытание физического объекта для получения высокой достоверности о его характеристиках; оптимизационные, связанные с нахождением оптимальных показателей системы (например, нахождение минимальных затрат или определение максимальной прибыли).
По наличию воздействий на систему модели делятся на детерминированные (в системах отсутствуют случайные воздействия) и стохастические (в системах присутствуют вероятностные воздействия). Эти же модели некоторые авторы классифицируют по способу оценки параметров системы: в детерминированных системах параметры модели оцениваются одним показателем для конкретных значений их исходных данных; в стохастических системах наличие вероятностных характеристик исходных данных позволяет оценивать параметры системы несколькими показателями.
По отношению ко времени модели разделяют на статические, описывающие систему в определенный момент времени, и динамические, рассматривающие поведение системы во времени. В свою очередь, динамические модели подразделяют на дискретные, в которых все события происходят по интервалам времени, и непрерывные, где все события происходят непрерывно во времени.
По возможности реализации модели классифицируются как мысленные, описывающие систему, которую трудно или невозможно моделировать реально, реальные, в которых модель системы представлена либо реальным объектом, либо его частью, и информационные, реализующие информационные процессы (возникновение, передачу, обработку и использование информации) на компьютере. В свою очередь, мысленные модели разделяют на наглядные (при которых моделируемые процессы и явления протекают наглядно);
символические (модель системы представляет логический объект, в котором основные свойства и отношения реального объекта выражены системой знаков или символов) и математические (представляют системы математических объектов, позволяющие получать исследуемые характеристики реального объекта). Реальные модели делят на натурные (проведение исследования на реальном объекте и последующая обработка результатов эксперимента с применением теории подобия) и физические (проведение исследования на установках, которые сохраняют природу явления и обладают физическим подобием).
По области применения модели подразделяют на универсальные, предназначенные для использования многими системами, и специализированные, созданные для исследования конкретной системы.
Постановка задачи. Этот этап заключается в содержательной постановке задачи и определении конечных целей решения.
Построение математической модели (математическая формулировка задачи). Модель должна правильно (адекватно) описывать основные законы рассматриваемого процесса. Построение или выбор математической модели из существующих требует глубокого понимания проблемы и знания соответствующих разделов математики и физики.
Разработка численного метода. Поскольку ПК может выполнять лишь простейшие операции, то он «не понимает» постановки задачи в математической формулировке. Для ее решения должен быть найден численный метод, позволяющий свести задачу к некоторому вычислительному алгоритму. Специалисту-прикладнику для решения задачи, как правило, необходимо из имеющегося арсенала методов выбрать тот, который пригоден в данном конкретном случае.
Разработка алгоритма и построение блок-схемы. Процесс решения задачи (вычислительный процесс) записывается в виде последовательности элементарных арифметических и логических операций, приводящий к конечному результату и называемый алгоритмом решения задачи. Алгоритм можно изобразить в виде блок-схемы.
Программирование. Алгоритм решения задачи записывается на понятном машине языке в виде программы на каком-либо алгоритмическом языке (Pascal, Fortran, C++, MATLAB).
Отладка программы. Составленная программа содержит разного рода ошибки, неточности, описки. Отладка программы на компьютере включает контроль программы, диагностику ошибок, их исправление. Программа испытывается на решении контрольных (тестовых) задач для получения уверенности в достоверности результатов.
Проведение расчетов. На этом этапе готовятся исходные данные для расчетов, и проводится счет по отлаженной программе.
Анализ результатов. Результаты расчетов тщательно анализируются, оформляются научно-техническая документация.
Различают два вида погрешностей — абсолютную и относительную. Абсолютная погрешность некоторого числа равна разности между его истинным значением и приближенным значением, полученным в результате вычисления или измерения. Относительная погрешность — это отношение абсолютной погрешности к приближенному значению числа.
1. Погрешности, связанные с самой постановкой математической задачи. Математические формулировки редко точно отображают реальные явления: обычно они дают лишь более или менее идеализированные модели. Как правило, при изучении тех или иных явлений природы мы вынуждены принять некоторые, упрощающие задачу, условия, что вызывает ряд погрешностей (погрешности задачи).
Иногда бывает и так, что решить задачу в точной постановке трудно или даже невозможно. Тогда ее заменяют близкой по результатам приближенной задачей. При этом возникает погрешность, которую можно назвать погрешностью метода.
2. Погрешности, связанные с наличием бесконечных процессов в математическом анализе. Функции, фигурирующие в математических формулах, часто задаются в виде бесконечных последовательностей или рядов (например, sin х = х – х3/3! + х5/5! - …). Более того, многие математические уравнения можно решить, лишь описав бесконечные процессы, пределы которых и являются искомыми решениями.
Так как бесконечный процесс, вообще говоря, не может быть завершен в конечное число шагов, то мы вынуждены остановиться на некотором члене последовательности, считая его приближением к искомому решению. Понятно, что такой обрыв процесса вызывает погрешность, называемую обычно ocтaточной погрешностью.
3. Погрешности, связанные с наличием в математических формулах числовых параметров, значения которых могут быть определены лишь приближенно. Таковы, например, все физические константы. Условно эта погрешность называется начальной.
4. Погрешности, связанные с системой счисления. При изображении даже рациональных чисел в десятичной системе или другой позиционной системе справа от запятой может быть бесконечное число цифр (например, может получиться бесконечная десятичная периодическая дробь). При вычислениях, очевидно, можно использовать лишь конечное число этих цифр. Так возникает погрешность округления. Например, полагая 1/3= 0,333, получается погрешность ∆ ≈3· 10-4. Приходится так же округлять и конечные числа, имеющие большое количество знаков.
5. Погрешности, связанные с действиями над приближенными числами (погрешности действий). Понятно, что, производя вычисления с приближенными числами, погрешности исходных данных в какой-то мере переносятся в результат вычислений. В этом отношении погрешности действий являются н е у с т р а н и м ы м и.
Устойчивость. Малые погрешности в исходной величине приводят к малым погрешностям в решении.
Если исходная величина имеет абсолютную погрешность ∆х, то решение имеет погрешность ∆у. Отсутствие устойчивости означает, что даже незначительные погрешности в исходных данных приводят к большим погрешностям в решении или даже к неверному результату.
Корректность. Задача называется поставленной корректно, если для любых значений исходных данных из некоторого класса ее решение существует, единственно и устойчиво по исходным данным. Численный алгоритм (метод) называется корректным в случае существования и единственности численного решения при любых значениях исходных данных, а также в случае устойчивости этого решения относительно погрешностей исходных данных.
Понятие сходимости. При анализе точности вычислительного процесса одним из важнейших критериев является сходимость численного метода. Она означает близость получаемого численного решения задачи к истинному решению.
В общем случае нелинейное уравнение можно записать в виде:
F(x)=0. (1.1)
где функция F(x) определена и непрерывна на конечном или бесконечном интервале [а,ь]. Решить такое уравнение - это значит установить, имеет ли оно корни, сколько корней, и найти значения корней с заданной точностью. Задача численного нахождения действительных и комплексных корней уравнения (1.1) обычно состоит из двух этапов:
Отделение корней, т. е. нахождение достаточно малых окрестностей рассматриваемой области, в которых содержится одно значение корня.
Уточнение корней, т. е. вычисление корней с заданной степенью точности в некоторой окрестности.
Пусть имеется уравнение F(x)=0, причем можно считать, что все интересующие вычислителя корни находятся на отрезке [А; В], в котором функция F(x) определена, непрерывна и F(A)*F(B)< 0. Требуется отделить корни уравнения, т. е. указать все отрезки [а; b]с[А; B], содержащие по одному корню. Будем вычислять значения F(x), начиная с точки х=А, двигаясь вправо с некоторым шагом h. Как только обнаружится пара соседних значений F(x), имеющих разные знаки, и функция f(x) монотонна на этом отрезке, так соответствующие значения аргумента х (предыдущее и последующее) можно считать концами отрезка, содержащего корень.
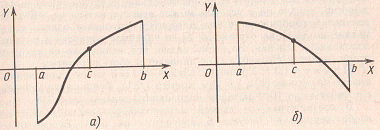
Пусть уравнение (1.1) имеет на отрезке [а;b] единственный корень причем функция F(x) на этом отрезке непрерывна. Разделим отрезок [а; b] пополам точкой с = (а + b)/2. Если F(c) ≠0 (что практически наиболее вероятно), то возможны два случая: либо F(x) меняет знак на отрезке [a;c] (рис 3, а), либо на отрезке [с; b] (рис. 3, б). F(a)*F(с)<0. Выбирая в каждом случае тот из отрезков, на котором функция меняет знак, и продолжая процесс половинного деления дальше, можно дойти до сколь угодно малого отрезка, содержащего корень уравнения.
Основная идея метода заключается в следующем: задаётся начальное приближение вблизи предположительного корня, после чего строится касательная к исследуемой функции в точке приближения, для которой находится пересечение с осью абсцисс. Эта точка и берётся в качестве следующего приближения. И так далее, пока не будет достигнута необходимая точность.
Задача о приближении (аппроксимации) функций: данную функцию f(x) требуется приближенно заменить (аппроксимировать) некоторой функцией φ(x) так, чтобы отклонение (в некотором смысле) φ(x) от f(x) в заданной области было наименьшим. Функция φ(х) при этом называется аппроксимирующей.
Пусть есть таблица из N точек и значений функции в этих точках.
Интерполяция - приближение функции кривой, проходящей через все N точек. Основной недостаток интерполяционных алгоритмов в том, что при изменении значения функции в одной точке необходимо полностью пересчитать интерполяционные формулы.
Аппроксимация - приближение кривой, не обязательно проходящей через все точки.
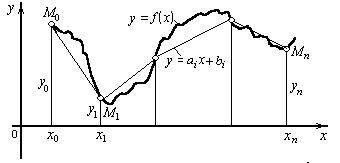
Простейшим и часто используемым видом локальной интерполяции является линейная интерполяция. Она состоит в том, что заданные точки М(xi, yi) (i = 0, 1, ..., n) соединяются прямолинейными отрезками, и функция f(x) приближается к ломаной с вершинами в данных точках.
Уравнения каждого отрезка ломаной линии в общем случае разные. Поскольку имеется n интервалов (xi , xi + 1), то для каждого из них в качестве уравнения интерполяционного полинома используется уравнение прямой, проходящей через две точки. В частности, для i - го интервала можно написать уравнение прямой, проходящей через точки (xi , yi) и (xi + 1, yi + 1), в виде:
![]()
В качестве интерполяционной функции на отрезке [xi-1; xi+1] принимается квадратный трехчлен. Такую интерполяцию называют также параболической.
Уравнение
квадратного трехчлена
![]() (1.4)
содержит три неизвестных коэффициента
аi,
bi,
сi,
для определения которых необходимы три
уравнения. Ими служат условия прохождения
параболы (1.4) через три точки
(1.4)
содержит три неизвестных коэффициента
аi,
bi,
сi,
для определения которых необходимы три
уравнения. Ими служат условия прохождения
параболы (1.4) через три точки
(хi-1;
yi-1),
(xi;
yi),
(xi+1;
yi+1).
Эти условия можно записать в виде
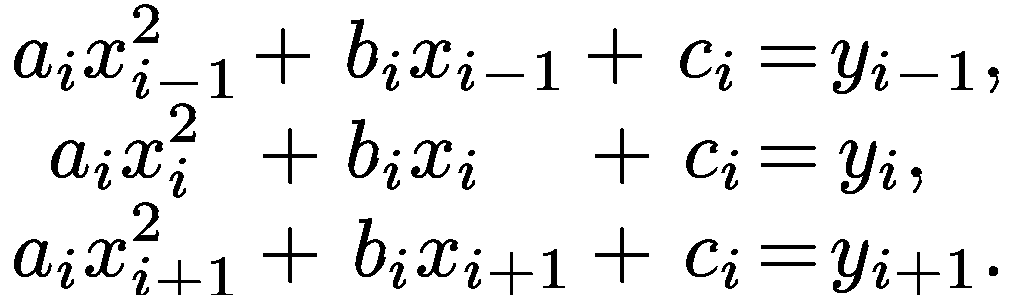 (1.5)
(1.5)
Интерполяция
для любой точки x
![]() [x0,
xn]
проводится по трем ближайшим точкам.
[x0,
xn]
проводится по трем ближайшим точкам.
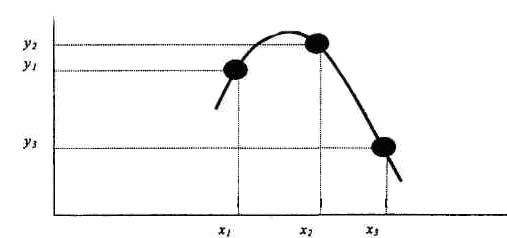
Рис.8
Предположим теперь, что точек несколько, например пять. В этом случае для каждой последовательной тройки точек можно найти свое уравнение параболы из условия ее прохождения через соответствующие три точки. Результирующая функция состоит из отрезков парабол. Это - кусочно-параболическая интерполяция (рис.9)
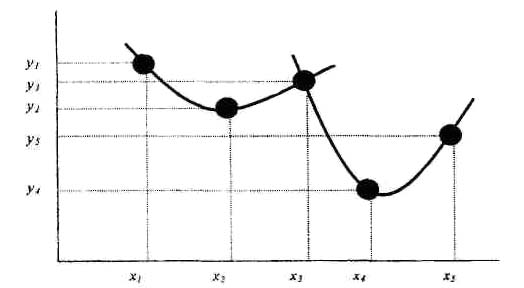
Рис.9
Искомое выражение для производной k-то порядка в некоторой точке х = xi представляется в виде линейной комбинации заданных значений функции в узлах x0, х1, ... , хn:
![]() (1.6)
(1.6)
Предполагается,
что это соотношение выполняется точно,
если функция у
является многочленом степени не выше
n,
т. е. может быть представлена
в виде

Отсюда следует, что соотношение (1.6), в частности, должно выполняться точно для многочленов у = 1, у = х - х0, ... , у = (х – х0)n. Подставляя последовательно эти выражения в (1.6) и требуя выполнения точного равенства, получаем систему n + 1 линейных алгебраических уравнений для определения неизвестных коэффициентов c0, c1, ... , сn.
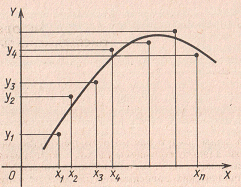
Пусть в результате измерений в процессе опыта получена таблица некоторой зависимости f:

Вид приближающей функции F можно определить следующим образом. По таблице строится точечный график функции f, а затем проводится плавная кривая, по возможности наилучшим образом отражающая характер расположения точек
Рассмотрим
один из распространенных способов
нахождения формулы (1.7). Предположим,
что приближающая функция F в точках х1,
х2,
…, хn
имеет значения
![]() (1.8)
(1.8)
Требование близости табличных значений у1, у2, ... , уn и значений (1.8) можно истолковать следующим образом. Будем рассматривать совокупность значений функции f из таблицы и совокупность (1.8) как координаты двух точек n-мерного пространства. С учетом этого задача приближения функции может быть переформулирована следующим образом: найти такую функцию F заданного вида, чтобы расстояние между точками М(у1, у2, ... , уn)
и М’( ) было наименьшим.
![]()
Многие инженерные задачи, задачи физики, геометрии и многих других областей человеческой деятельности приводят к необходимости вычислять определенный интеграл вида
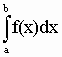 (1.9) где f(x) данная функция, непрерывная
на отрезке [a; b].
(1.9) где f(x) данная функция, непрерывная
на отрезке [a; b].
вычисление интеграла равносильно вычислению площади криволинейной трапеции.
Метод левых прямоугольников
Разделим
отрезок [a; b] на n равных частей, т.е. на n
элементарных отрезков. Длина каждого
элементарного отрезка
![]() .
Точки деления будут: x0=a;
x1=a+h;
x2=a+2×
h, ... , xn-1=a+(n-1)×
h; xn=b.
Эти числа будем называть узлами. Вычислим
значения функции f(x) в узлах, обозначим
их y0,
y1,
y2,
... , yn.
Cтало
быть,
y0=f(a),
y1=f(x1),
y2=f(x2),
... , yn=f(b).
Числа y0,
y1,
y2,
... , yn
являются ординатами точек графика
функции, соответствующих абсциссам x0,
x1,
x2,
... , xn.
Площадь криволинейной трапеции
приближенно заменяется площадью
многоугольника, составленного из n
прямоугольников. Таким образом, вычисление
определенного интеграла сводится к
нахождению суммы n элементарных
прямоугольников.
.
Точки деления будут: x0=a;
x1=a+h;
x2=a+2×
h, ... , xn-1=a+(n-1)×
h; xn=b.
Эти числа будем называть узлами. Вычислим
значения функции f(x) в узлах, обозначим
их y0,
y1,
y2,
... , yn.
Cтало
быть,
y0=f(a),
y1=f(x1),
y2=f(x2),
... , yn=f(b).
Числа y0,
y1,
y2,
... , yn
являются ординатами точек графика
функции, соответствующих абсциссам x0,
x1,
x2,
... , xn.
Площадь криволинейной трапеции
приближенно заменяется площадью
многоугольника, составленного из n
прямоугольников. Таким образом, вычисление
определенного интеграла сводится к
нахождению суммы n элементарных
прямоугольников.
![]()