16-17.

Степенной ряд есть функциональный ряд с общим членом f_n (y) = a_n( y – y₀ )ⁿ (n = 0, 1, 2, …) (a_n — действительные числа):

              a_n( y – y₀ )ⁿ = a₀ + a₁( y – y₀ ) + a₂( y – y₀ )² + … + a_n( y – y₀ )ⁿ + …

   Действительное число y₀ называется центром степенного ряда. Заменой переменного x = y – y₀ этот степенной ряд преобразуется в степенной ряд

              a_n xⁿ = a₀ + a₁ x + a₂ x² + … + a_n xⁿ + …

с нулевым центром. В дальнейшем ограничимся исследованием рядов именно такого вида. 

   Существуют степенные ряды, которые

а) сходятся при всех x (всюду сходящиеся степенные ряды), например  ;

б) сходятся только при x = 0, например   n! xⁿ;

в) для некоторых x ≠ 0 сходятся, для других расходятся, например   xⁿ. 

   Свойства степенных рядов.

1. Если степенной ряд   a_n xⁿ сходится при x₁, то он абсолютно сходится для всех x, удовлетворяющих неравенству | x | < | x₁ |, а если степенной ряд расходится при x₂, то он расходится и для всех х, удовлетворяющих неравенству | x | > | x₂ |.

2. Если степенной ряд   a_n xⁿ при некоторых x ≠ 0 сходится, а при остальных расходится, то существует, и притом только одно, положительное число r такое, что степенной ряд при | x | < r сходится, и даже абсолютно, а при | x | > r расходится. При x = r и x = – r ряд может как сходиться, так и расходиться. Число r называют радиусом сходимости степенного ряда. Если r > 0, то промежуток (– r, r) называется интервалом сходимости степенного ряда.

Для вычисления радиуса сходимости используется теорема Коши – Адамара: радиус r сходимости ряда   a_n xⁿ равен обратной величине верхнего предела последовательности { }:

            r = 

(при этом r = ∞, если   = 0, и r = 0, если   = ∞).

Верхний предел r числовой последовательности {b_n} есть верхняя граница «сгущения» последовательности, т. е. для любого ε > 0 существует только конечное число индексов n таких, что b_n > r + ε, но для бесконечного числа n справедливо неравенство b_n > r – ε. Если для любого действительного числа C имеется бесконечное множество индексов n таких, что b_n > C, то говорят, что верхний предел равен + ∞; если напротив, имеется только конечное число индексов n таких, что b_n > C, то говорят, что верхний предел равен – ∞. Верхний предел существует всегда. Если существует  , то

              =  .

Радиус сходимости r степенного ряда   a_n xⁿ может быть вычислен также при помощи признака Даламбера: если существует предел  = q, то r =   (r = ∞ при q = 0 и r = 0 при q = ∞).

3. В каждой внутренней точке интервала сходимости степенной ряд сходится абсолютно. Во всяком замкнутом промежутке, который целиком лежит в интервале сходимости, степенной ряд сходится равномерно. Если степенной ряд сходится при x = r (не обязательно абсолютно), то степенной ряд на [0 , r] сходится равномерно. (Если степенной ряд расходится при x = r, то на отрезке [0 , r] степенной ряд не может сходится равномерно.)

4. Степенные ряды   a_n xⁿ и 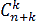  a_{n + k} xⁿ (k = 0, 1, 2, …) имеют один и тот же радиус сходимости, однако в граничных точках интервала сходимости ряды могут иметь различное поведение.

5. Теорема единственности разложения в степенной ряд. Если два ряда   a_n xⁿ и   b_n xⁿ сходятся в одном и том же интервале | x | < r и во всех его точках (или только в бесконечном подмножестве точек, имеющих нуль в качестве предельной точки) имеют одинаковые суммы, то эти суммы совпадают, т. е. a_n = b_n для n = 0, 1, 2, …

6. Если   a_n( x – x₀ )ⁿ — степенной ряд с радиусом сходимости r > 0, то его сумму f (x) можно разложить также в степенной ряд с центром в любой точке x₁ из интервала сходимости:

            f (x) =   b_n( x – x₁ )ⁿ, где b_n =   a_{n + m}( x – x₁ )^m.

При этом все ряды, которые представляют b_n, сходятся (см. свойство 4), а для радиуса сходимости r₁ нового ряда справедливо неравенство

            r₁ ≥ r – | x – x₀ |.

7. а) Сумма f (x) степенного ряда   a_n xⁿ для всех значений x из интервала сходимости (– r, r) есть непрерывная функция. Если степенной ряд сходится при x = r, то сумма f (x) при этом значении x также непрерывна (слева):

              f (x) =   a_n rⁿ.

Если степенной ряд сходится при x = – r, то сумма f (x) при x = – r непрерывна справа (теорема Абеля о предельном значении).

б) Степенной ряд   a_n xⁿ всегда можно почленно интегрировать на отрезке [0, x₁], где | x₁ | < r:

              f (t) dt =   a_n   tⁿ dt =   a_n  ;

при этом x₁ может совпадать с одним из концов интервала сходимости, если степенной ряд сходится в этой точке.

в) Степенной ряд   a_n xⁿ внутри его интервала сходимости можно почленно дифференцировать:

            f ' (x) =   a_n   =   n a_n x^{n – 1}.

Это утверждение верно также и для концов интервала сходимости, если ряд   n a_n x^{n – 1} сходится в этих точках. Степенной ряд внутри интервала сходимости можно дифференцировать любое число раз:

            f ^(k) (x) =     a_n x^{n – k} = k!     a_{n + k} xⁿ.

8. Действия со степенными рядами.

а) Если f (x) =   a_n xⁿ и g (x) =   b_n xⁿ, то для любого x, являющегося внутренней точкой интервалов сходимости обоих рядов, можно построить сходящиеся ряды

            f (x) ± g (x) =   (a_n ± b_n) xⁿ ,  f (x) · g (x) =   a_m b_{m – n}   xⁿ.

б) Пусть g (x) — сумма степенного ряда с радиусом сходимости r : g (x) =   b_n xⁿ, а f (u) — сумма степенного ряда с радиусом сходимости r' : f(u) =   a_n uⁿ. Тогда F (x) = f (g (x)) снова есть сумма некоторого степенного ряда: F (x) = c_n xⁿ — по крайней мере для тех x, для которых ряд   |b_n xⁿ| сходится и имеет сумму, меньшую, чем r'. Коэффициенты c_n вычисляются при помощи рядов: c_n =   a_m b_mn которые абсолютно сходятся при условии, что | b₀ | < r', где (g (x))^k =   b_kn xⁿ. Другими словами, чтобы получить степенной ряд F (x), можно подставить u =   b_nxⁿ в степенной ряд   a_n uⁿ и привести подобные члены.

в) Если функция f (x) в окрестности нулевой точки есть сумма степенного ряда   a_n xⁿ и f (0) – a₀ ≠ 0, то функция   в окрестности нулевой точки есть сумма некоторого степенного ряда   c_n xⁿ; так как для малых x оба ряда сходятся, то

            1 =   · f (x) =     a_m c_{n – m}   xⁿ,

и согласно теореме о единственности разложения функции в степенной ряд выполняются соотношения

            1 = a₀ c₀, 0 =   a_m c_{n – m} при n ≥ 1;

отсюда можно найти c_n. Точно так же можно представить отношение двух функций g/f, являющихся суммами степенных рядов, как сумму степенного ряда   c_n xⁿ в некоторой окрестности нуля, если a₀ = f (0) ≠ 0. Коэффициенты c_n вычисляются из соотношения

              =   c_n xⁿ

            или   b_n xⁿ =     a_n xⁿ       c_n xⁿ  ,

т. е. из системы b_n =  a_m c_{n – m} для n = 0, 1, 2, …

18. Ряд Тейлора в окрестности точки a имеет виды:

1)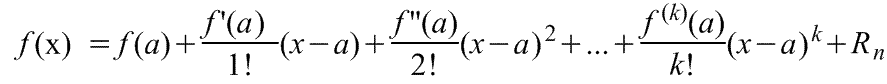 , где f(x) - функция, имеющая при х=а производные всех порядков. R_n - остаточный член в ряде Тейлора определяется выражением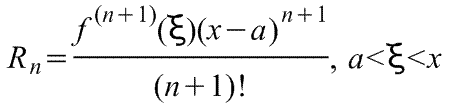 

2)

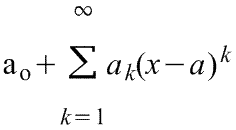
k-тый коэффициент (при х_k) ряда определяется формулой

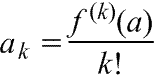
3) Частным случаем ряда Тейлора является ряд Маклорена (=Макларена) (разложение происходит вокруг точки а=0)

при a=0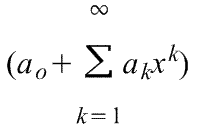 

члены ряда определяются по формуле

Условия применения рядов Тейлора.

1. Для того, чтобы функция f(x) могла быть разложена в ряд Тейлора на интервале (-R;R) необходимо и достаточно, чтобы остаточный член в формуле Тейлора (Маклорена (=Макларена)) для данной функции стремился к нулю при k→∞ на указанном интервале (-R;R).

2. Необходимо чтобы существовали производные для данной функции в точке, в окрестности которой мы собираемся строить ряд Тейлора.

Свойства рядов Тейлора.

1. Если f есть аналитическая функция, то ее ряд Тейлора в любой точке а области определения f сходится к f в некоторой окрестности а.

2. Существуют бесконечно дифференцируемые функции, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности а. Например:

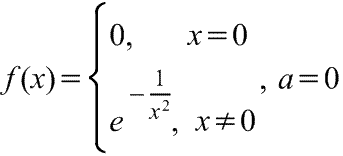
Маклорена ряд, исторически неправильное название (по имени К. Маклорена) степенного ряда вида:

 ,

где f(0), f’(0), f”(0), ..., f⁽ⁿ⁾(0),... – значения заданной функции f(x) и её последовательных производных при х = 0.Этот ряд был получен ранее Маклорена английским математиком Б. Тейлором (опубликовал 1715), что было известно и самому Маклорену. М. р. есть частный случай Тейлора ряда.

19. Функция f(x) = e^x.

 

  Находим: f(x) = e^x,  f(0) = 1

f¢(x) = e^x,  f¢(0) = 1

f⁽ⁿ⁾(x) = e^x, f⁽ⁿ⁾(0) = 1

Тогда:  

Функция f(x) = sinx.

 

  Получаем f(x) = sinx; f(0) = 0

  f¢(x) = cosx = sin( x + p/2); f¢(0) = 1;

  f¢¢(x) = -sinx = sin(x + 2p/2); f¢¢(0) = 0;

  f¢¢¢(x) = -cosx = sin(x + 3p/2); f¢¢¢(0)=-1;

  …………………………………………

  f⁽ⁿ⁾(x) = sin(x + pn/2);  f⁽ⁿ⁾(0) = sin(pn/2);

  f⁽ⁿ⁺¹⁾(x) = sin(x + (n + 1)p/2); f⁽ⁿ⁺¹⁾(e) = sin(e + (n + 1)p/2);

 

Итого: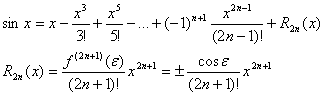  

 

 

Функция f(x) = cosx.

 

  Для функции cosx, применив аналогичные преобразования, получим:

 

 

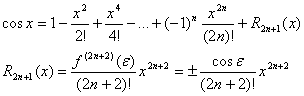
20.Функция f(x) = (1 + x)^a.

(a - действительное число)

 

25. Дифференциальное уравнение вида

или

называется дифференциальным уравнением с разделяющимися переменными.

Заметим, что в данных дифференциальных уравнениях каждая из функций зависит только от одной переменной, т.е. происходит разделение переменных.

Для решения такого дифференциального уравнения необходимо домножить или разделить обе части дифференциального уравнения на такое выражение, чтобы в одну часть уравнения входили только функции от   и   , в другую часть уравнения - только функции от   ,   . Затем в полученном дифференциальном уравнении надо проинтегрировать обе части:

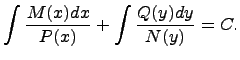
Следует заметить, что при делении обеих частей дифференциального уравнения на выражение, содержащее неизвестные   и   , могут быть потеряны решения, обращающие это выражение в ноль.

Обратим внимание, что дифференциальные уравнения с разделяющимися переменными легко сводятся к интегрированию. В общем случае получаем получаем дванеопределенных интеграла.

26. Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643—1727). Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации. Метод обладает квадратичной сходимостью. Улучшением метода является метод хорд и касательных. Также метод Ньютона может быть использован для решения задач оптимизации, в которых требуется определить нуль первой производной либо градиента в случае многомерного пространства.

Чтобы численно решить уравнение   методом простой итерации, его необходимо привести к следующей форме:  , где   — сжимающее отображение.

Для наилучшей сходимости метода в точке очередного приближения   должно выполняться условие  . Решение данного уравнения ищут в виде  , тогда:

В предположении, что точка приближения «достаточно близка» к корню  , и что заданная функция непрерывна  , окончательная формула для   такова:

С учётом этого функция   определяется выражением:

Эта функция в окрестности корня осуществляет сжимающее отображение^[1], и алгоритм нахождения численного решения уравнения   сводится к итерационной процедуре вычисления:

28. Метод половинного деления

Его ещё называют методом дихотомии. Этот метод решения уравнений отличается от выше рассмотренных методов тем, что для него не требуется выполнения условия, что первая и вторая производная сохраняют знак на интервале [a, b]. Метод половинного деления сходится для любых непрерывных функций f(x) в том числе недифференцируемых.

Разделим отрезок [a, b] пополам точкой  . Если  (что практически наиболее вероятно), то возможны два случая: либо f(x) меняет знак на отрезке [a, c] (Рис. 3.8), либо на отрезке [c, b] (Рис. 3.9)

Рис. 3.8

Рис. 3.9

Выбирая в каждом случае тот отрезок, на котором функция меняет знак, и продолжая процесс половинного деления дальше, можно дойти до сколь угодно малого отрезка, содержащего корень уравнения.

Пример 4. Уравнение 5^x - 6x -3 = 0 имеет единственный корень на отрезке [1;2]. Решить это уравнение методом половинного деления.

29. Приближенное вычисление функций является важной практической задачей. Для большинства случаев практических вычислений бывает достаточно уже реализованных в программных системах функций, которые, кстати, также вычисляются приближенно. Однако, если необходимо вычислять эти функции с точностью, отличной от предлагаемой, или реализовать нестандартную функцию, то непременно возникает задача приближенного вычисления. Ниже описаны несколько подходов к решению данной задачи.

Интерполяция степенным рядом

Известно, что любую аналитическую функцию f(x) можно разложить в степенной ряд в окрестности некоторой точки x₀.

По известному разложению легко вычислить значение полинома, составленного из первых k членов степенного ряда в заданной точке. В общем случае вопрос о выборе числа k для достижения необходимой точности вычислений совсем не прост. Стандартная практика завершать вычисление суммы, когда модуль последнего добавленного слагаемого в определенное число раз меньше модуля накопленной суммы. К счастью, часто используемые в вычислениях элементарные функции разложимы в ряд Тейлора, хотя, как будет показано ниже, и для таких функций метод интерполяции ограниченным степенным рядом не дает желаемых результатов.

Для разложения функции f(x) в ряд Тейлора в окрестности точки x₀

cправедлива следующая оценка остаточного члена:

,

откуда можно найти число членов ряда, доставляющее необходимую точность приближения значения функции в точке х.

К недостаткам данного метода можно отнести наличие радиуса сходимости степенного ряда для разложения в окрестности точки x₀. Обычно радиус сходимости степенного ряда известен заранее, и с этой проблемой справляются путем замены переменной, внося ошибки округления. Но, гораздо более коварная ситуация возникает со всюду сходящимися рядами, так как зачастую они сходятся настолько медленно, что становятся непригодными для вычислений. Кроме того, абсолютная ошибка вычислений по указанной формуле распределена неравномерно и нарастает по мере удаления от точки x₀.