Вопросы на экзамен по геометрии.
Определение декартовой системы координат на плоскости. Определение Вектора. Равенство векторов. Свободный вектор.
Декардовая система координат на плоскость - пара перпендикулярных направленный прямых с указанным на них масштабом.
Вектор - упорядоченная пара точек (фиксированный вектор).
AB и CD, не лежащие на одной прямой, называются равными, если фигура ABCD - параллелограмм.
AB и CD, лежащие на одной прямой, называются равными, если существует такой вектор MN, не лежащий на одной прямой, что ABNM и CDNM - параллелограммы.
Свободный вектор - класс эквивалентности векторов. Класс равных векторов, называется свободный вектором. (Любой свободный вектор можно отложить от любой точки)
Координаты вектора – разность координат его конца и начала.
Определение суммы векторов (сложение векторов), умножение вектора на число. Свойства сложения и умножения. Действие с векторами в координатах.
Сложение векторов (по правило параллелограмма):
1) по правило треугольника:
Д
ля
сложения двух векторов U
и V по правилу треугольника
оба эти вектора переносятся параллельно
самим себе так, чтобы начало одного из
них совпадало с концом другого. Тогда
вектор суммы задаётся третьей стороной
образовавшегося треугольника, причём
его начало совпадает с началом первого
вектора, а конец с концом второго вектора.
2)по правилу параллелограмма:
Д
ля
сложения двух векторов V
и U по правилу параллелограмма
оба эти вектора переносятся параллельно
самим себе так, чтобы их начала совпадали.
Тогда вектор суммы задаётся диагональю
построенного на них параллелограмма,
исходящей из их общего начала.
Умножение на число:
Произведение вектора a(a1; a2) на число λ называется вектор (λa1; λa2), т.е. (a1; a2) λ = (λa1; λa2).
Для любого вектора a и чисел λ, μ
Для любого вектора a и b и числа λ
Свойства сложения векторов – Для любых векторов а b с заданных в пространстве, справедливы равенства
Переместительный закон
Сочетательный закон
Свойства умножения векторов – Для любых векторов и и любых чисел k, m справедливы равенства:
Сочетательный закон
Первый распределительный закон
Второй распределительный закон
Действия с векторами в координатах –
Сложение
При сложении векторов их соответстветственные
координаты складываются.
Вычитание
При вычитании векторов их соответстветственные
координаты вычитаются.
Умножение
При умножении вектора на число все его
координаты умножаются на это число.
Деление отрезка в данном отношении и доказательство этой формулировки. (Если даны две точки A,B …)
(1)
1)
АВ
2)АВ=ОВ-ОА
3)АС=
ОС=ОА+АС=ОА+
=
ов+(1+
)=
ОВ+
(2)
Физический
смысл деления отрезка в 
Базисы на плоскости и в пространстве (опр). Док-ть: что любой вектор раскладывается по базису.
Базисы на плоскости и пространстве - произвольная пара н7е параллельных не нулевых векторов.
Если дан базис, то любой вектор можно
представить в виде 
(Пр) разложение вектора (2,-1) по базису (1,5),(-2,5)
Базис в пространстве - упорядоченная тройка ненулевых некомпланарных векторов. (компланарный - лежит в одной плоскости)
Определение скалярного произведения векторов. Запись скалярного произведения в координатах.
Скалярное произведение векторов - произведение их моделуй на cos угла между ними.
Если
векторы a и b
заданы своими
координатами: 
и 
,
то их скалярное произведение может
быть вычислено по формуле 
.
Формулировка и док-во свойств скалярного произведения.
Пусть a, b, c -3 вектора. Тогда
Док-во:
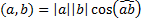
если
По свойству длины:
,
т.о. 
4)
n
Определение векторного произведения. Его корректность.
Векторное произведение векторов a b R3
называется вектор c R3, такой что
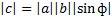
орт 
,
орт 
;
вектора
образуют правую тройку;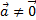 
≠ 
,
и
не параллельны,
то 
=
Запись векторного произведения в координатах.
=
Док-во:
=
=
=
+
+
=
=1
- 
-
)=
после
несложных преобразований получим
равенство 
=
2)Проверим
┻
,
┻
=
)=
=0
если всё раскрыть получим 0
+
+
=0
3)Проверим,
что
,
,
образуют правую тройку
1) Пару
,
можно непр. деформ. перевести в пару
i=
и j=
в проц деформ вектора остаются независимыми
2)добиваемся чтобы вектора лежали в ХУ
3
)
направлен по оси Х
4
)
лежал в верхней полуплоскости
5)сжимая
и растягивая вектора совмещаем их с
,
,
смысл тройки ( , , ) сохраняется
=
= (0,0,1)=