
Лекция 11. Преобразования Лапласа
В
данной лк напомним известные нам из
ТФКП преобразования Лапласа L[1]=F
(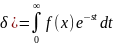 (11) формула образующая преобразование
Лапласа имеет вид:
(11) формула образующая преобразование
Лапласа имеет вид:
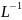 [F]=f(z)=
[F]=f(z)=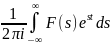
Преобразования
Лапласа имеет важнейшее преимущество
перед преобразованием Фурье ,поскольку
в его формулу входит быстро убывающий
множитель
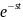 и поэтому оно применимо к более широкому
классу функций затем мы решим несколько
важных задач для уравнений частных
производных и обыкновенных дифференциальных
уравнений.
и поэтому оно применимо к более широкому
классу функций затем мы решим несколько
важных задач для уравнений частных
производных и обыкновенных дифференциальных
уравнений.
П.11.1. свойства преобразований Лапласа
Преобразования Лапласа позволяют свести обыкновенные дифуры к алгебраическим. Это мы проиллюстрируем дальше ,более того преобразования Лапласа позволяют преобразовывать уравнения с частными производными в обыкновенные дифуры.
Свойство1(теорема11.1):достаточное условие преобразования Лапласа Е или:
1)для
любого положительного числа А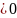 функция ф(t)
кусочно-непрерывная на интервале t
функция ф(t)
кусочно-непрерывная на интервале t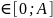
2)существуют
такие константы:
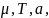 что
:
что
: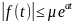
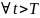 то преобразование Лапласа:
то преобразование Лапласа:
L[f(t)]=F(s)=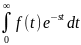 существует при всех S
существует при всех S
Свойство2.преобразования
Лапласа с частных производных .Пусть
u(x,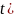 функция двух переменных ,мы хотим найти
результаты применения на преобразование
Лапласа к различным частным производным
функция двух переменных ,мы хотим найти
результаты применения на преобразование
Лапласа к различным частным производным
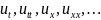 т.к
преобразования Лапласа производ. по
переменной t-переменная
интегрирования),то правое преобразование
Лапласа выглядит так:
т.к
преобразования Лапласа производ. по
переменной t-переменная
интегрирования),то правое преобразование
Лапласа выглядит так:
L[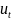 ]=
]=
L[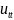 ]=
]=
L[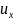 ]=
]=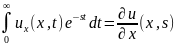
L[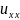 ]=
]=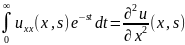
4.
f(t)=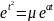 -преобразование
Лапласа данной функции не существует
-преобразование
Лапласа данной функции не существует
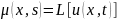
Правила
преобразований
и
вытекает из теоремы о дифференцировании
по параметру :
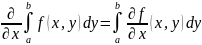 формула для преобразования преобразований
и
можно получить интегрировав по частям.
формула для преобразования преобразований
и
можно получить интегрировав по частям.
Свойство3.(теорема о свертке)
Определение:конечная
свертка двух функций по t
определена формулами: (f*g)(t)=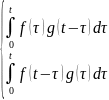 эти интегралы равны.
эти интегралы равны.
Пример1.посчитать свертку: f(t)=t, g(t)=t
(f*g)(t)=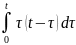 =
=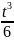
Важнейшие свойства свертки определяются формулой : L[f*g]=L[f]L[g] (3)
Ими
эквивалентны функции:
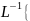 L[f]L[g]
}= f*g
(4)
L[f]L[g]
}= f*g
(4)
Эти формулы позволяют превращать преобразования Лапласа для произведения двух функций ,т.е: L[f]-L[g] ,если прообр. Каждой известен,после того как f и g найдены,то можно найти их свертку
Пример2. Найти свертку
[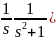
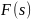 =
=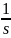 G(s)
G(s)
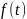 =1
g(t)=
=1
g(t)=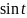
=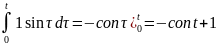
П.11.2.теплопроводность в полубесконечной среде
Рассмотрим
глубокий резервуар с жидкостью и пусть
боковая поверхность резервуара
теплоизолирована.пусть
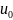 -начальная
температура жидкости и пусть температура
воздуха над жидкостью равна нулю.
-начальная
температура жидкости и пусть температура
воздуха над жидкостью равна нулю.
А)тепло течет внутрь,если u(0,t)<0 и наружу,если: u(0,t)>0
Б)резервуар настолько глубокий,что граничные результаты на дно не влияют на решение при интересующих нас значений x.наша задача найти температурное поле в жидкости на различных глубинах и в различные моменты времени,другими словами нами нужно решить задачу:
(УЧП):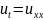
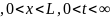
(ГУ):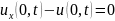
(НУ):
u(x,0)=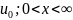 (5)
(5)
Для
решения этой задачи применим преобразования
Лапласа (по переменной t),но
можно также и по x
,т.к x<[0,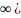 .
После применения преобразований приходим
к обыкновенному диф. уравнению по
переменной x:
.
После применения преобразований приходим
к обыкновенному диф. уравнению по
переменной x:
ОДУ:
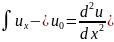
ГУ:
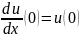
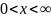 (6)
(6)
Мы
преобразовали только уравнение и
граничное условие без начального условия
,у нас получилось обыкновенное ДУ с
одним граничным условием,второе условие
можно записать из физического смысла
u(x)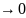 при x
при x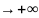
u(x,s)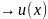 -для
упрощения
-для
упрощения
решаем
уравнение (6): u(x)=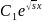 +
+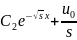 ,находим теперь
,находим теперь
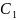 и
и
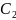 из
граничных условий.
из
граничных условий. ,
т.к t
не должно увеличиваться ,определяем
константу
из граничного условия точки x=0
,получаем u(x)=
,
т.к t
не должно увеличиваться ,определяем
константу
из граничного условия точки x=0
,получаем u(x)=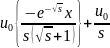
erf-график интеграла вероятности и дополнительная функция к нему erfc
теперь
последний шаг: для определения
температурного поля u(x,t)
необходимо вычислить u(x,t)=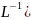 u(x,s)]
u(x,s)]
для обращения преобразования Лапласа воспользуемся таблицей ,которая вскоре будет приведена:
u(x,t)=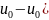 ]
]
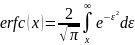 -это
функция дополнительного интеграла
вероятности
-это
функция дополнительного интеграла
вероятности
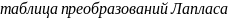
f(t)= F(s)] |
F(s)=L[f(t)] |
1. 1 |
, s>0 |
2.
|
|
3.
|
|
4.
|
|
5.
|
|
6. erfc |
|
7.
|
|
8. f(at) |
|
9.
|
F(s-a) |
10. f(t)g(t) |
F(S)G(S) |
11.
|
|
П.11.3. применение преобразований Лапласа к решению обыкновенных ДУ
Покажем технику преобразований Лапласа к решению обыкновенных ДУ на следующем простом уравнение.
Пример2.
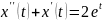
X(0)=0,

Применим преобразования Лапласа к обеим частям уравнения , учитывая что:
L
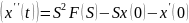
L
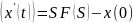
L(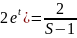 , F(s)=L[x(t)]
, F(s)=L[x(t)]
Подставляем
начальные значения в уравнение ,получим
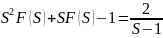
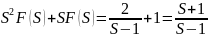
F(S)(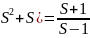
Находим
от сюда F(S):
F(S)=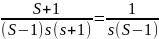
Сейчас
нужно применить обратное преобразование
Лапласа для начала разложим дробь
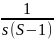 в сумму двух простейших дробей:
в сумму двух простейших дробей:
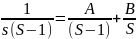
AS+BS-B=1
S:A+B=0
 :-В=1,
В=-1
А=1
:-В=1,
В=-1
А=1
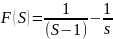
F(s)]=
]
-
]=
Ответ: x(t)=
Замечание:этот пример можно решить обычным методом ,используя характер уравнения и квазиполином Эйлера.
Лекция 12. Краевые задачи
П.12.1.постановка краевой задачи.
На ряду
с обычной задачей Коши,т.е когда заданы
начальные данные иногда приходится
решать так называемую краевую или
граничную задачу. Задача эта состоит в
том ,что заданные условия не в одной
точке
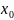 ,а в двух
,а в двух
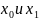 ,которые
являются концами отрезка. Задачи о
движении тела массы m под
действием заданной силы F(t,
,которые
являются концами отрезка. Задачи о
движении тела массы m под
действием заданной силы F(t,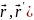 .
Часто надо найти такой
.
Часто надо найти такой
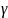 и движение,чтобы тело переместилось из
точки А в точку В,т.к в момент времени
и движение,чтобы тело переместилось из
точки А в точку В,т.к в момент времени
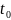 находилось в точке А,а в момент времени
t в точке В.задача сводиться
к интегрированию дифференциального
уравнения движения:
находилось в точке А,а в момент времени
t в точке В.задача сводиться
к интегрированию дифференциального
уравнения движения: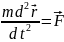 (t,
.
(t,
.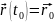 ,
,
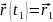
Эта задача имеет не единственные решения,если речь идет об эллистической задаче на замкнутой поверхности ,то тело может попасть в одну и ту же точку по навесной и настильной траектории. Более того при очень больших начальных скоростях тело может попасть туда же,облетев один или несколько раз земной шар . Такую задачу можно поставить для луча света,проходящего через преломляющую среду ,надо найти направление ,чтобы выйдя из точки А он попал в точку В. Задача эта также может иметь несколько решений в частности ,если В находится в фокусе линзы ,сначала нужно найти общие решения дифуры,затем чтобы решить краевую задачу нужно подставить граничное условие и определить произвольные константы. При этом не всегда существует действительное решение ,если же оно существует ,то не всегда существенное.
Пример1. Решить краевую задачу
 +
+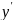 =0,
y(0)=0, y(
=0,
y(0)=0, y(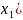 =
=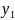 (1) -
(1) -
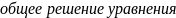
Y=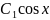 +
+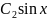 y(0)=
y(0)=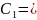 0
0
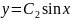
y(
=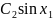 =
=
если
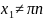 ,то
тогда найдется
=
,то
тогда найдется
=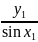
то решение краевой
задачи имеет вид y=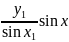 ,если же
,если же
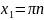 и
и
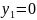 ,то
все функции вида y=
являются решениями ,если же
,то
все функции вида y=
являются решениями ,если же
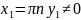 ,то
решений нет.
,то
решений нет.
П.12.2 Краевая задача для линейных уравнений 2 порядка
Пусть
задана краевая задача вида:
+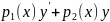 =
=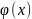 (2)
(2)
y(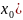 =
=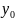 , y(
=
(3)
, y(
=
(3)
делаем
линейную замену переменных z=y-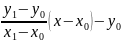 z(
=0,
z(
=0
z(
=0,
z(
=0
Краевые
условия (3) сводятся при этом к нулевым
условиям. Линейное уравнение (2) не
нарушается. Умножаем уравнение (2) на
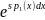
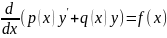 (4)
(4)
 ,поэтому без ограничения общности мы
можем вместо задачи (2) с краевыми
условиями (3) решать задачу (4) y(
=
y(
=0
(5) сначала рассмотрим задачу (4),где
является локанизованной в точке x=s
функции с единичным импульсом .Более
точно рассмотрим уравнение
,поэтому без ограничения общности мы
можем вместо задачи (2) с краевыми
условиями (3) решать задачу (4) y(
=
y(
=0
(5) сначала рассмотрим задачу (4),где
является локанизованной в точке x=s
функции с единичным импульсом .Более
точно рассмотрим уравнение
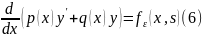
С граничными
условиями y(
=
y(
=0,где
функция
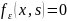 на
всем отрезке x
на
всем отрезке x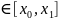 за исключением точки x=s
за исключением точки x=s
s-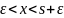
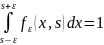
обозначим
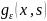 непрерывное решение этой краевой задачи
не перейдем к пределу при
непрерывное решение этой краевой задачи
не перейдем к пределу при
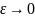 и получим
и получим
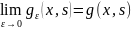 (7)
(7)
можно
доказать существование этого предела
не зависящего от функции
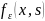 .
.
Далее в
этой Лк мы зададим определение функции
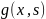 которая называется функцией влияния
или функцией Грина этой краевой задачи.
Решение краевой задачи (2) с непрерывной
функцией f(x)
можно рассматривать как суперпозицию
решения краевых задач соответствующе
локализованным в точке функции с
импульсом f (
которая называется функцией влияния
или функцией Грина этой краевой задачи.
Решение краевой задачи (2) с непрерывной
функцией f(x)
можно рассматривать как суперпозицию
решения краевых задач соответствующе
локализованным в точке функции с
импульсом f (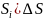 , где
, где
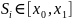 -точки
деления отрезка на m равных
частей
-точки
деления отрезка на m равных
частей
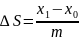 .
Тогда приближенное решение краевой
задачи (2) и (3) равно интегральной сумме
:
.
Тогда приближенное решение краевой
задачи (2) и (3) равно интегральной сумме
: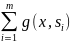 f (
,
а предел этой суммы при m
f (
,
а предел этой суммы при m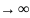 y(x)=
y(x)=
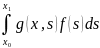 (8) является решением рассматриваемой
краевой задачи . то можно передать
решение (8) и функции влияния
(8) является решением рассматриваемой
краевой задачи . то можно передать
решение (8) и функции влияния
 следующий физический смысл : в уравнение
(6) рассмотрим y(x)
как смещение некоторой системы под
влиянием непрерывно распределенной на
отрезке
следующий физический смысл : в уравнение
(6) рассмотрим y(x)
как смещение некоторой системы под
влиянием непрерывно распределенной на
отрезке
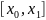 силы F(x).
Например отклонение струны от положения
равновесия под влиянием распределенной
нагрузки с плотностью f(x).
Тогда
силы F(x).
Например отклонение струны от положения
равновесия под влиянием распределенной
нагрузки с плотностью f(x).
Тогда
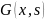 описывает смещение вызываемое единичной
сосредоточенной силы примененной в
точке x=s, а
решение (8) рассматривается как предел
суммы решений соответствующих
сосредоточенным силам.
описывает смещение вызываемое единичной
сосредоточенной силы примененной в
точке x=s, а
решение (8) рассматривается как предел
суммы решений соответствующих
сосредоточенным силам.
Функция Грина обладает следующими свойствами ,которые вытекают из ее определения (7):
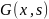 непрерывная по x при
фиксированном s
непрерывная по x при
фиксированном s
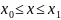 ,
,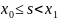
является решением соответствующего однородного уравнения
 на всем отрезке от
на всем отрезке от
 за исключением точки x=s.
Т.к вне этой точки правая часть равна
нулю.
за исключением точки x=s.
Т.к вне этой точки правая часть равна
нулю.удовлетворяют граничным условиям
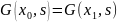 =0
=0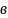 точке
x=s производная
точке
x=s производная
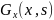 u*x=s
должна иметь разрыв 1 рода со скачком
u*x=s
должна иметь разрыв 1 рода со скачком
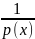 .
Действительно можно ожидать разрыв
только в точке локализации при x=s.
Умножим тождество
.
Действительно можно ожидать разрыв
только в точке локализации при x=s.
Умножим тождество
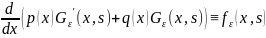 на dx и проинтегрируем в
пределах s-
на dx и проинтегрируем в
пределах s-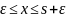
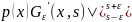 +
+ dx=1
dx=1
переходя
к пределу , где
,получим [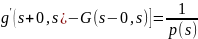
все эти рассуждения о функции Грина носили характер ,теперь предадим им точность
Определение:функция Грина краевые задачи (4),(5) называется функция удовлетворяющая условию 1,2,3,4, подставляя в уравнение (4) и проверяем ,что функция (9) является решением этого уравнения :
Y(x)=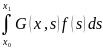 (9) при этом краевые условия (5)
удовлетворяются в силу свойства (3)
(9) при этом краевые условия (5)
удовлетворяются в силу свойства (3)
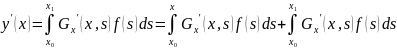
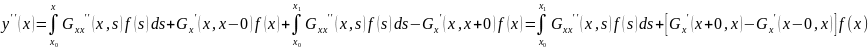
Подставляя
уравнение (9) в уравнение (4) получим
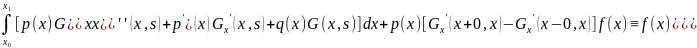
В силу
условий 2 и 4. Рассмотрим метод построения
функции Грина из которого следует также
достаточное условие ее существования
. рассмотрим решение
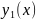 уравнения
уравнения
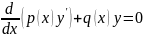 (10)
(10)
Определяемое
начальными условиями
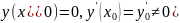 это решение не удовлетворяет второму
граничном условию y(
это решение не удовлетворяет второму
граничном условию y(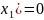 . решение
. решение
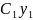 (x),
где
(x),
где
 -произвольная
постоянная также удовлетворяет граничному
условию
-произвольная
постоянная также удовлетворяет граничному
условию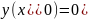 аналогично находим не тривиальное
решение
аналогично находим не тривиальное
решение
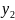 (x)
в уравнение (10),удовлетворяющее второму
граничному условию
(x)
в уравнение (10),удовлетворяющее второму
граничному условию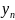 (
,этому
же условию удовлетворяют все решения
семейства
(
,этому
же условию удовлетворяют все решения
семейства
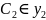 (x),
где
(x),
где

Функцию
Грина получим в таком виде :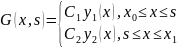
Причем
постоянные
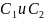 выбираем так,чтобы были выполнены
условия 1 и 4,т.е чтобы функция
выбираем так,чтобы были выполнены
условия 1 и 4,т.е чтобы функция
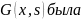 не
прерывна по x при
фиксированном s и в
частности не прерывна в точке x=s
не
прерывна по x при
фиксированном s и в
частности не прерывна в точке x=s
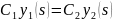 (11) и чтобы
(11) и чтобы
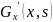 в точке x=s
имела скачок
в точке x=s
имела скачок
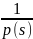 :
:
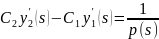 (12)
(12)
В силу
предположения
(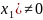 решение
решение
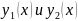 линейно независимы ,т.к все линейно
зависящие от
линейно независимы ,т.к все линейно
зависящие от
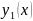 решения имеют вид
решения имеют вид
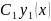 и не обращаются в нуль в точке
и не обращаются в нуль в точке
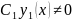 ,а
,а
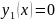 .
Значит определить системы (11) и(12)
являющийся вранскианом W(
.
Значит определить системы (11) и(12)
являющийся вранскианом W(
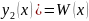 в точке x=s
не равен нулю W(s)
в точке x=s
не равен нулю W(s)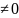 .
Тогда легко находятся
.
Тогда легко находятся
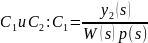 ,
,
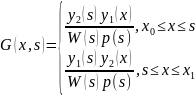 (13)
(13)
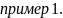 Найти
функцию Грина краевой задачи
Найти
функцию Грина краевой задачи
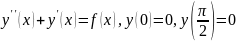
решение
однородного уравнения ,удовлетворяющего
условию
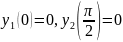
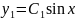 ,
,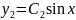
По функции
(13): W(x)=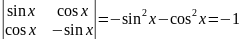
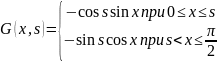
Замечание:мы
предполагаем ,что нет не тривиального
решения y(x)
однородного уравнения (10) , удовлетворяющего
нулевым граничным условиям
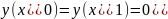 это условие гарантирует не только
существование и единственность функции
Грина. если бы существовали функции
Грина
это условие гарантирует не только
существование и единственность функции
Грина. если бы существовали функции
Грина
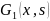 и
и
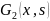 для краевой задачи (4) и (5) получилось бы
два решения этой задачи :
для краевой задачи (4) и (5) получилось бы
два решения этой задачи :
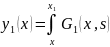 f(s)ds
,
f(s)ds
,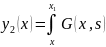 f(s)ds
f(s)ds
Разность
которых
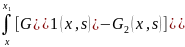 f(s)ds
вопреки предположению будет решением
однородного уравнения ,образуещемся в
нуль в точке
и
f(s)ds
вопреки предположению будет решением
однородного уравнения ,образуещемся в
нуль в точке
и
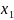 .
.
Лекция 13. Специальные функции математической функции
Под специальной функцией можно понимать любую функцию ,которая не изучается в школьном курсе алгебры.В данной лекции мы изучим основные специальные функции и дифуры решениями которых они являются.
П.13.1 Гамма-функция
N! обозначает произведение чисел n=1*2*3…n
Функцию фактериал можно записать рекурсивной записью (n+1)!=(n+1)n!
Теперь мы хотим найти функцию Г(z),которая удовлетворяет условию : Г(z+1)= Г(z)*z (1)
Будем
искать решение этого уравнения в виде
интеграла Лапласа: Г(z)=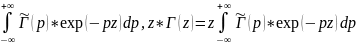 =
=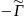 (p)
(p)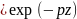 +
+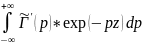 (2)
(2)
Предположим ,что образ Гфункции таков, что в ней интеграл слагаемое (2)=0,Левая часть неравенства (1) может быть записана:
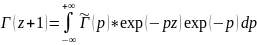 для Г(p)
(1):
для Г(p)
(1):
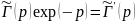 это уравнение легко решается:
это уравнение легко решается:
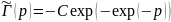 C-const
C-const
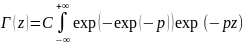 dp
dp
 переменных
t=
переменных
t=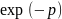
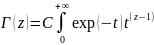 dt
(3)
dt
(3)
Постоянная
С выбирается так,чтобы при целых t
Г-функция совпадала с фактериалом
Г(n+1)=n!
:
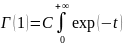 dt
= -С
dt
= -С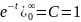
В
итоге получаем формулу Эйлера
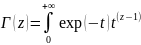 dt
эта функция часто встречается в
математических текстах можно проверить
,что функция (4)удовлетворяет уравнению
(1),проинтегрировав правую часть по
частям (4) и тогда:
dt
эта функция часто встречается в
математических текстах можно проверить
,что функция (4)удовлетворяет уравнению
(1),проинтегрировав правую часть по
частям (4) и тогда:
Г(z)= +
+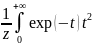 dt=
dt=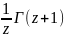
Справедлива
dt
(4) Г(z)Г(1-z)=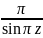 (5)
(5)
Г-функцию
можно представить в вид бесконечного
произведения в формуле (4) представить: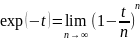 тогда интегральное представление
Г-функции будет таким : Г(z)=
тогда интегральное представление
Г-функции будет таким : Г(z)=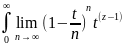 dt
в этой формуле можно поменять можно
поменять местами предел несобственного
интеграла и предел при нем стремиться
к бесконечности.Вообще это тонкий
вопрос,но в этом случае поменять можно:
Г(z)=
dt
в этой формуле можно поменять можно
поменять местами предел несобственного
интеграла и предел при нем стремиться
к бесконечности.Вообще это тонкий
вопрос,но в этом случае поменять можно:
Г(z)=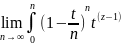 dt
возьмем этот интеграл по частям :
dt
возьмем этот интеграл по частям :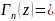
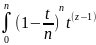 dt=
dt=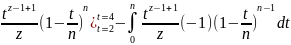
Если
провести эту процедуру n
раз: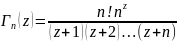 ,переходя к пределу получим предельную
форму Эйлера для Г-функции: Г(z)=
,переходя к пределу получим предельную
форму Эйлера для Г-функции: Г(z)=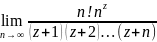 (6)
(6)
П.13.2
 Гипергеометрическая функция
Гипергеометрическая функция
Гипергеометрическая функция-это обобщение геометрической прогрессии. Она обладает рядом замечательных свойств. И интересует математиков около двух веков. В связи с ее изучением Гаус занялся вопросом сходимости рядов,а Риман –аналитическим продолжением сходящихся функций.
Гипергеометрическая функция обладает следующими замечательными свойствами F(a,b,c,z) зависит от 4-х параметров :
1)
F(1,b,b,z)=
2)zF(1,1,2,-z)=
3)F(-n,b,b,t)=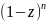
4)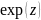 =
=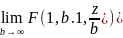
Это
значит что многие элементарные функции
выражаются через гипергеометрические
с определенным набором параметров .эту
функцию можно разложить в ряд по степеням
z
с параметрами F(a,b,c,z)=1+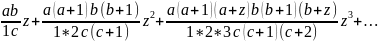 (7)
(7)
Название
гипергеометрический этому ряду дал
Валлис в 1655 позже его изучали Эйлер и
Кумляр . однако только Гаус доказал что
сходимость и следовательно коротко
гипергеометрический ряд можно записать
так: F(a,b,c,z)=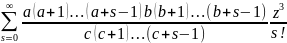 (7)
(7)
Здесь
предполагается ,что с
, с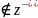 ,воспользовавшись
признаком Даламбера для сходимости
рядов легко показать ,что радиус
сходимости ряда (7) равен единице. Эйлером
получены интегральные представления
произведения Г-функций: Г(p)Г(q)=Г(p+q)
,воспользовавшись
признаком Даламбера для сходимости
рядов легко показать ,что радиус
сходимости ряда (7) равен единице. Эйлером
получены интегральные представления
произведения Г-функций: Г(p)Г(q)=Г(p+q)
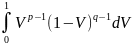 (8) Re(p)>0,
Re(V)>0.
Эйлер используя это представление
,выразил эту интегральную функцию через
Г-функцию: F(a,b,c,z)=
(8) Re(p)>0,
Re(V)>0.
Эйлер используя это представление
,выразил эту интегральную функцию через
Г-функцию: F(a,b,c,z)= dt
эта формула позволяет продолжить
функцию F(a,b,c,z)
во внешность единичного круга
dt
эта формула позволяет продолжить
функцию F(a,b,c,z)
во внешность единичного круга
Определение:гипергеометрическим
уравнением называется уравнение вида
z(1-z)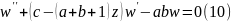 c
помощью прямой подстановки ряда (7) и
(10) можно убедиться ,что гипергеометрическая
функция является решением
гипергеометрического уравнения
c
помощью прямой подстановки ряда (7) и
(10) можно убедиться ,что гипергеометрическая
функция является решением
гипергеометрического уравнения
П.13.3. Функция Бесселя
Определение:функция
Бесселя имеет вид:
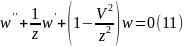
Можно
искать решение того уравнения в виде
степенного ряда ,т.о. переходим к функции
Бесселя:
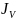 (z)=
(z)= (12)
(12)
Параметр
V
называется порядком
функции Бесселя ,z-аргументом.Воспользовавшись
признаком Даламбера мохно доказать
,что ряд (12)сходится,если V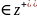 (целое положительное число),то функция
Бесселя-целая функция.Если V
(целое положительное число),то функция
Бесселя-целая функция.Если V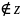 ,тогда
функция Бесселя имеет точку ответвления
z=0.
Главная ветвь функции Бесселя определяется
главной ветвью функции
,тогда
функция Бесселя имеет точку ответвления
z=0.
Главная ветвь функции Бесселя определяется
главной ветвью функции
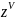 .Связь
различных ветвей функции Бесселя дает
формулу :
.Связь
различных ветвей функции Бесселя дает
формулу :
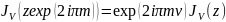 выясним как связаны между собой функции
Бесселя различных порядков .Единственное
что у нас определение (12) им и воспользуемся
:
выясним как связаны между собой функции
Бесселя различных порядков .Единственное
что у нас определение (12) им и воспользуемся
:
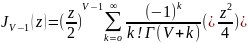 заменим Г –функцию
по формуле Г(V+k+1)=(V+k)Г(V+k)
заменим Г –функцию
по формуле Г(V+k+1)=(V+k)Г(V+k)
Получим
цепочку:
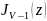 =
)
=V(
=
)
=V(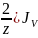 (z)+
(z)+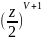
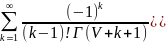
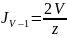 -
-
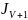 (13)
(13)
Эта
и есть та формула ,которая связывает
функции Бесселя различных порядков.
Интегральное представление функции
Бесселя имеет вид:
(z)=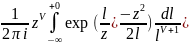
П.13.4 понятие о явлении Стокса
Проще
всего понять явление Стокса на следующем
явлении:
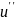 -
-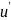 =0
u=ch(z)=
=0
u=ch(z)=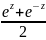
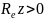
В
секторе
,т.е в правой полуплоскости это решение
асимптотическое при
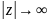 ведет себя как
ведет себя как
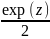 в секторе действительная часть
в секторе действительная часть
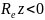 ,т.е
в левой полуплоскости
,т.е
в левой полуплоскости
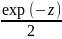 .
Это значит что асимптотика является
скачком при непрерывном изменении
аргумента z(arg
z)
в этом и состоит явление Стокса.
.
Это значит что асимптотика является
скачком при непрерывном изменении
аргумента z(arg
z)
в этом и состоит явление Стокса.
П.13.5 Функция Вейерштрасса
В
этом пункте мы будем изучать решение
дифур 1 порядка
=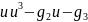 (14)
оно появляется если интегрировать
уравнение 2 порядка с квадратичной
нелинейностью:
(14)
оно появляется если интегрировать
уравнение 2 порядка с квадратичной
нелинейностью:
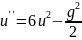
В
уравнение (14) легко разделяются переменные
dz=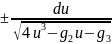 дальше нужно интегрировать это уравнение
,здесь возникают некоторые неясности
,что означает
дальше нужно интегрировать это уравнение
,здесь возникают некоторые неясности
,что означает
 параметр Y
лежит на двулистной Римановой
поверхности?здесь недостаточно задать
значение функции y
в некоторой точке
параметр Y
лежит на двулистной Римановой
поверхности?здесь недостаточно задать
значение функции y
в некоторой точке
 нужно еще задать знак
нужно еще задать знак
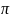 или
-,т.е выбрать лист римановой поверхности.
или
-,т.е выбрать лист римановой поверхности.
z=
u/
=
-знак
перед корнем –это условие лишнее.
Выберем для простоты в качестве начальной
точки ветвления z=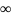 .
Тогда z=
-
.
Тогда z=
-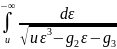
Функция
u=p(z)
обратная к этому элимптическому интегралу
,называется p-функция
Вейерштрасса .не все пути на римановой
поверхности эквивалентны ,обозначим
через
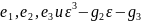 =0.
Пусть
=0.
Пусть
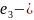 вещественный
корень (
вещественный
корень (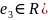 .Соединим
на римановой поверхности разрезом
.Соединим
на римановой поверхности разрезом
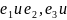 .
Цикл на верхнем листе поверхности
обходящим отрезок
.
Цикл на верхнем листе поверхности
обходящим отрезок
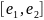 назовем а-периодом .Цикл соединяющий
два разреза и проходящий по верхнему и
нижнему листу поверхности b-периодом.можно
видеть что любой путь
на римановой поверхности можно представить
в виде пути не обходящего не один цикл
назовем а-периодом .Цикл соединяющий
два разреза и проходящий по верхнему и
нижнему листу поверхности b-периодом.можно
видеть что любой путь
на римановой поверхности можно представить
в виде пути не обходящего не один цикл
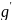 и сумму конечного числа обходов по a
и b
циклом
и сумму конечного числа обходов по a
и b
циклом
 .
Это означает ,что функция B-двоякопериодическая
,а числа :2
.
Это означает ,что функция B-двоякопериодическая
,а числа :2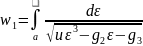 ,
2
,
2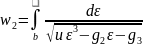 (15)-периоды этой функции. т.е p(z+m
(15)-периоды этой функции. т.е p(z+m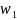 +n
+n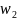 )=P(z)
Если бы отношения этих двух чисел было
бы вещественным,то двоякой периодичности
быть не могло бы. Т.к вещественный период
может быть только один. Здесь однако
отношение этих чисел является комплексным
числом.p-функцию
B
можно представить в виде ряда:
)=P(z)
Если бы отношения этих двух чисел было
бы вещественным,то двоякой периодичности
быть не могло бы. Т.к вещественный период
может быть только один. Здесь однако
отношение этих чисел является комплексным
числом.p-функцию
B
можно представить в виде ряда:
p(z)=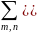 ]
(16)
]
(16)
п.13.6. Эллиптическая функция.
Рассмотрим
уравнение движения математического
маятника которое имеет вид:
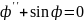 (17), умножим уравнение на
(17), умножим уравнение на
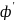 и проинтегрируем по t
в результате получим : 1/2
и проинтегрируем по t
в результате получим : 1/2 -
-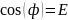 (18)
(18)
Решение
уравнения математического маятника
можно записать в виде : t+
=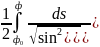 сделаем замену ku=
сделаем замену ku=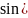 ,k=sin(
,k=sin(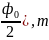 огда
kdu=
огда
kdu=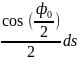
ds=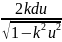 решение уравнения математического
маятника выражается через интеграл
вида: t=
решение уравнения математического
маятника выражается через интеграл
вида: t=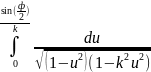 (19) теперь удобно рассматривать функцию
обратную интегралу как новую специальную
функцию u=sn
(19) теперь удобно рассматривать функцию
обратную интегралу как новую специальную
функцию u=sn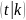 ,
,
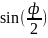 =u
sin(
=u
sin(
определение:эта
новая функция называется синусом
амплитуды или синусом Якоби. обозначим
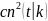 =1-
=1-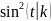 ,
d
,
d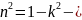
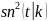
определение: функция sn называется косинусом амплитуды или косинусом Якоби ,а dn -дельтаамплитудой.
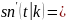 cn
cn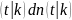
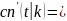 -sn
-sn
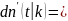 -
-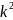 sn
sn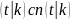
Значит
тройка функций cn,sn,dn
удовлетворяет системе уравнений
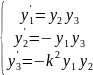 (21)
(21)
C
начальными условиями легко получаемые
из интегрального представления sn
:
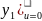 =0;
=0;
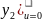 =1;
=1;
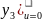 =1
(22)
=1
(22)
П.13.7. тэта -функция
Существует
несколько тэта-функций мы рассмотрим
в качестве основной тэта-функцию:
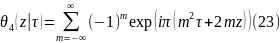
Легко
видеть,что для сходимости ряда(23)
необходимо и достаточно,чтобы
действительная часть
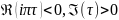
Функцию
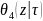 легко переписать в виде сходящегося
тригонометрического ряда:
легко переписать в виде сходящегося
тригонометрического ряда:
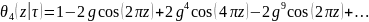 g=exp(-i
g=exp(-i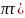
Из этой формулы ьлегко видеть что -четная функция,периодическая функция от z.
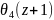 =
=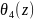 Функция
-частное
решение дифференциального уравнения
частных производных:
Функция
-частное
решение дифференциального уравнения
частных производных:
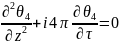 это легко проверить прямой подстановкой:
это легко проверить прямой подстановкой:
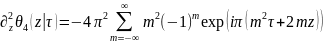
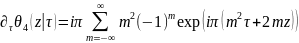
Для удобства вычислений обычно вводят еще три тэта-функции:
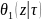 =-i
exp(i
=-i
exp(i =-i
=-i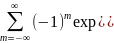
 =
=
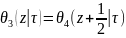 =
=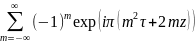
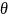 функция квазипериодична по
функция квазипериодична по
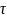 :
:
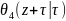 =
= =
=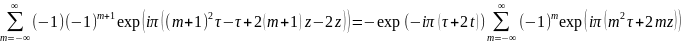
Подобные
вычисления показывают: :
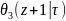 =
=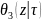
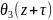 =exp(-i
=exp(-i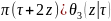
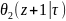 =
=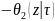 ;
;
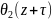 =
exp(-i
=
exp(-i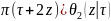
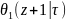 =
=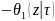 ;
;
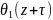 =
exp(-i
=
exp(-i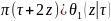
Справедлива формула приведения связывающая тэта-функции между собой:
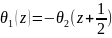 =-iM
=-iM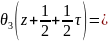 iM
iM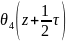
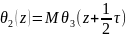 =M
=M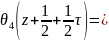

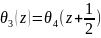 =M
=M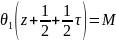
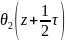
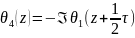 =iM
=iM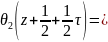
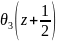
M=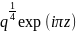
Эти неравенства легко получить воспользовавшись определениями тэта-функций.
Лекция 14. Понятия интегрального уравнения
П. 14.1. Классификация интегральных уравнений.
Интегральным
уравнением называется уравнение,содержащее
неизвестную функцию под знаком
интеграла,например у(х)=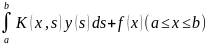 (1)
(1)
Y(x)=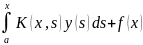 (2).
(2).
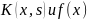 -заданные
функции, у(х)-искомое решение. Функция
К(x,s) в
приведенных соотношениях называется
ядром интегрального уравнения. В
уравнениях (1) и(2) явл-ся линейными
интегральными уравнениями встречаются
нелинейные уравнения:y(x)=
-заданные
функции, у(х)-искомое решение. Функция
К(x,s) в
приведенных соотношениях называется
ядром интегрального уравнения. В
уравнениях (1) и(2) явл-ся линейными
интегральными уравнениями встречаются
нелинейные уравнения:y(x)=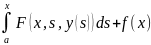
Линейные интегральные уравнения классифицируются так:
А)если
искомая функция содержится только
под знаком интеграла,то уравнение
называется интегральным уравнением
1 рода: (3);
(3);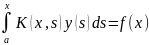 (4)
(4)
Уравнения (1) и (2) в которых неизвестная функция есть и не под интегралом называется уравнениями 2 рода
Б)если пределы интегрирования фиксированы,то интегральное уравнение называется уравнением Фредгольма
Если
пределы интегрирования переменные(в
случае (3),(4)),то уравнение называется
уравнением Вольтера. Формальное уравнение
Вольтера можно рассматривать как частный
случай уравнения Фредгольма,полагая
K(x,s)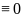 при S>x(в
формуле 2). Однако их физ. приложения
различны как и методы решения поэтому
их рассматривают отдельно.
при S>x(в
формуле 2). Однако их физ. приложения
различны как и методы решения поэтому
их рассматривают отдельно.
В)уравнения 1-4-однородные,если f(x) , в противном случае они называются неоднородными
П. 14.2 Физические примеры
Уравнение (2) сводится к задаче Коши для обыкновенного линейного дифференциального уравнения n порядка
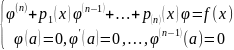 (5)
(5)
Положим
 (6), где y(x)-новая
неизвестная функция
(6), где y(x)-новая
неизвестная функция
Дифференцируя выражение (6) n раз:

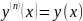
При этом
выполняются условия
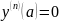
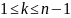 ,подставляя эти выражения для
,подставляя эти выражения для
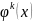 в левую часть уравнения (5) ,получим :
y(x)+
(7)
в левую часть уравнения (5) ,получим :
y(x)+
(7)
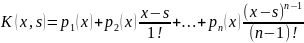
Значит задача 5 свелась к решению ИУ Вольтера 2 рода (7). Определив из (7) функцию y(x) находим f(x) из формулы (6)
К однородному
ИУ 2 рода (1) приводит к задаче о собственных
колебаниях системы, т.е колебания при
отсутствии внешней силы.Рассмотрим
задачи о малых поперечных свободных
колебаниях струны p(x).Пусть
концы струны закреплены,тогда для
поперечных отклонениях струны u(x,t)
выполнено p(x)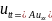 u(0,t)=0
u(l,t)=0
(8),где l-длина струны
u(0,t)=0
u(l,t)=0
(8),где l-длина струны
Определим
профиль струны при свободных гармонических
колебаниях ,т.е будем искать решение
вида: u(x,t)=g(x)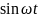 .
Значение
.
Значение
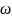 при
которой существует решение такого типа
называется собственными частотами
колебаний струны
при
которой существует решение такого типа
называется собственными частотами
колебаний струны
Для y(x)
из (8) получаем задачу:
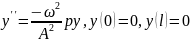 (9)
(9)
Правую
часть (9) рассматриваем как неоднородность,тогда
решение задачи (9) запишем в виде: y(x)=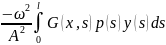 (10),где
-функция
Грина
(10),где
-функция
Грина
Значит задача свелась к нахождению max значений при которых существует нетривиальное решение однородного уравнения Фредгольма (10) и нахождению этих решений.

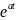
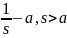


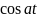
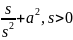
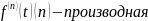


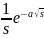
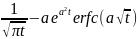
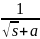

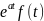
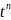 ,n
,n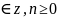
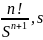 >0
>0