Кривые второго порядка

Будем рассматривать множества L точек евклидовой плоскости

Другое название для L - геометрическое место точек(ГМТ) в .

Будем считать, что на плоскости введена некоторая декартова прямоугольная система координат ХОУ

Координаты точки М принадлежащей плоскости , будем обозначать через х и у.

Определение. Уравнение данного ГМТ – это необходимое и достаточное условие принадлежности точки М(x,y) данному ГМТ, выраженное в форме уравнения или системы уравнений, роль неизвестной в котором или в которой играет сама точка или ее координаты в некоторой координатной системе.

Определение. Геометрическое место L точек(ГМТ) плоскости уравнение которого имеет вид

(1)

Пусть далее константы (вещественные числа ).

В уравнении (1) по крайней мере один из коэффициентов при старших членах отличен от нуля.( )

Иначе говоря кривая второго порядка - это такое ГМТ левая часть уравнения которого является полиномом второй сткепени от координат x y.

,

Три замечательных кривых

Гипербола

Определение. Гиперболой (Г) называется ГМТ плоскости, абсолютная величина разности расстояний от каждой из которых до двух фиксированных точек этой плоскости (называемых фокусами) есть величина постоянная, она меньше расстояний между фокусами.

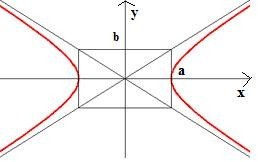
Осью гиперболы называется прямая, соединяющая её фокусы.

Расстояние от начала координат до одного из фокусов гиперболы называют фокусным расстоянием гиперболы .

Расстояние от начала координат до одной из вершин гиперболы называется большой или вещественной полуосью гиперболы .

Расстояние от вершины гиперболы до асимптоты вдоль направления параллельного оси ординат называется малой или мнимой полуосью гиперболы .

Отношение фокусного расстояния к большой полуоси гиперболы называется эксцентриситетом: . Эксцентриситет гиперболы всегда больше единицы.

Расстояние от фокуса до гиперболы вдоль прямой, параллельной оси ординат называется фокальным параметром ..

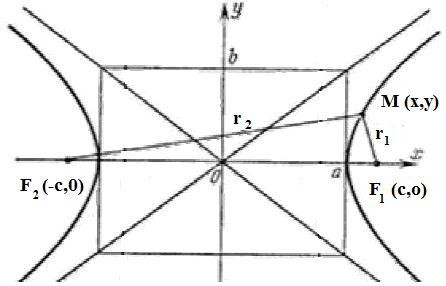
M(x, y) – точка на гиперболе, F₁, F₂ – фокусы гиперболы.

r_1, r₂ – расстояния от точки М до фокусов. 

По определению r₁ – r₂= 2a.  F₁F₂ = 2c. Выберем на гиперболе произвольную точку М(х, у).

Тогда:

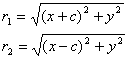
обозначим с² – а² = b² (геометрически эта величина – меньшая полуось) =>

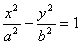
Получили каноническое уравнение гиперболы. Гипербола симметрична относительно середины отрезка, соединяющего фокусы и относительно осей координат.  Ось 2а называется действительной осью гиперболы.

Ось 2b называется мнимой осью гиперболы. Гипербола имеет две асимптоты, уравнения которых

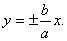
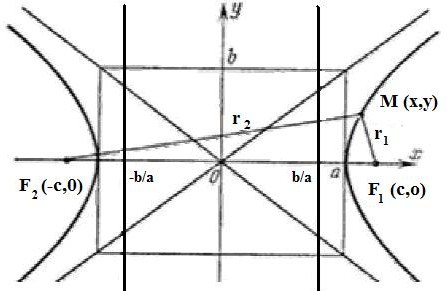
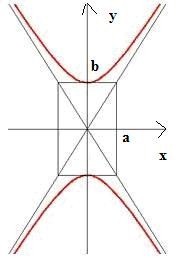<= Сопряженная гипербола

Эллипс

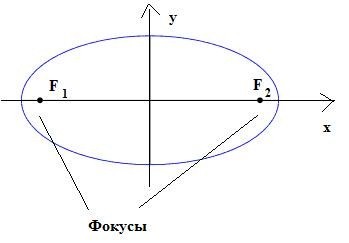
Определение. Эллипс (Э) - ГМТ в плоскости {Э}, сумма расстояний от каждой из которых до двух фиксированных точек F₁ и F₂ плоскости, называемых фокусами есть величина постоянная равная

Выводится каноническое уравнение эллипса аналогично каноническому уравнению гиперболы.

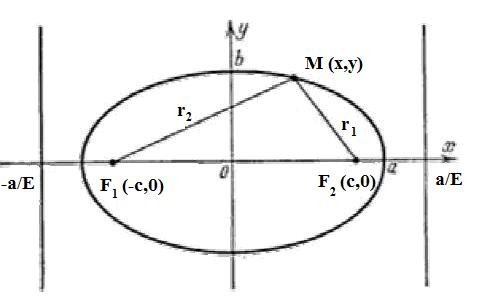
На основании определения эллипса составим его уравнение. Для этого выберем систему координат следующим образом. За ось Ox примем прямую, проходящую через фокусы F₁ и F₂, а за ось Oy – прямую, перпендикулярную к F₁F₂ и проведённую через середину отрезка F₁F₂ (рис. 2). Обозначим расстояние F₁F₂ между фокусами через 2с, тогда координаты фокусов будут: F₂ (с;0) и F₁(-с;0).

Возьмем на эллипсе произвольную точку M (x,y). Обозначим постоянную величину суммы расстояний от каждой точки до фокусов через 2а, тогда F₁M+ F₂M=2a (2)

По формуле расстояний между двумя точками найдём F₁M и F₂M.

Упростим выражения и получим:

, где

Это и будет каноническим уравнением эллипса.

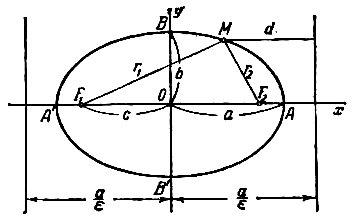
При указанном выборе системы координат оси координат являются осями симметрии эллипса, а начало координат - его центром симметрии (рис.). Точки, в которых эллипс пересекает свои оси, называются его вершинами. На рис. Вершины эллипса суть точки A’, A, B’, B. Часто осями эллипса называются также отрезки A’A=2a и B’B=2b; вместе с тем отрезок ОА=а называют большой полуосью эллипса, отрезок OB=b - малой полуосью.

Число

где а - большая полуось, называется эксцентриситетом эллипса. Очевидно, (для окружности ). Если М(x;y) - произвольная точка эллипса, то отрезки и (рис.) называются фокальными радиусами точки М. Фокальные радиусы могут быть вычислены по формулам

, .

Если эллипс определен уравнением (1) и , то прямые

,

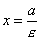
(рис.) называются директрисами эллипса (если , то директрисы определяются уравнениями , .

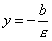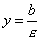Каждая директриса обладает следующим свойством: если r - расстояние от произвольной точки эллипса до некоторого фокуса, d - расстояние от той же точки до односторонней с этим фокусом директрисы, то отношение r к d (r/d) есть постоянная величина, равная эксцентриситету эллипса:

Пользуясь определением эллипса, его легко построить непрерывным движением карандаша. Для этого берём нерастяжимую нить длиной, равной большой оси эллипса, т.е. длиной 2а, и закрепляем концы этой нити в фокусах, положение которых предполагается известным.

Натягиваем нить карандашом и остриём его описываем кривую, держа нить всё время в натянутом состоянии. Кривая, описываемая при этом – эллипс, так как сумма расстояний от любой точки этой кривой до фокусов равна длине нити, т.е. равна постоянной величине.