
Основные свойства определителей.
Свойство 1. Определители квадратной матрицы и транспонированной матрицы равны.
Доказательство.
Пусть
- квадратная матрица и
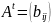 ,
где
,
где
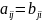 .
.
Тогда
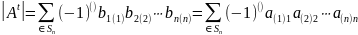 ,
переставив все сомножители каждого
слагаемого, упорядочив по первым
индексам, получим определитель
,
переставив все сомножители каждого
слагаемого, упорядочив по первым
индексам, получим определитель
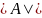 .
.
Свойство 2. При перестановке двух столбцов (строк) матрицы определитель меняет знак.
Доказательство.
Пусть
- квадратная матрица,
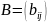 – матрица, полученная из матрицы
в результате перестановки двух столбцов
с индексами
– матрица, полученная из матрицы
в результате перестановки двух столбцов
с индексами
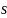 и
и
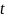 .
Пусть
- транспозиция из
,
переводящая
в
,
.
Пусть
- транспозиция из
,
переводящая
в
,
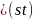 ,
тогда
,
тогда
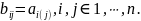
Поэтому
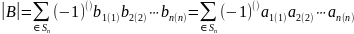 .
Учитывая, что транспозиция является
нечетной подстановкой, получим
.
Учитывая, что транспозиция является
нечетной подстановкой, получим
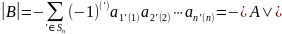 .
.
Свойство 3. Определитель матрицы, имеющей два одинаковых столбца (строки) равен нулю.
Доказательство.
Пусть матрица
имеет два одинаковых столбца, например
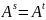 .
Обозначим соответствующую транспозицию
.
Тогда получим, что
.
Обозначим соответствующую транспозицию
.
Тогда получим, что
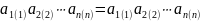 .
Следовательно, для любого слагаемого
определителя матрицы
найдется слагаемое этого же определителя,
содержащее те же самые элементы в
произведении, но с противоположным
знаком. Поскольку сумму определителя
можно разбить на соответственные пары,
то получим, что вся сумма равна 0.
.
Следовательно, для любого слагаемого
определителя матрицы
найдется слагаемое этого же определителя,
содержащее те же самые элементы в
произведении, но с противоположным
знаком. Поскольку сумму определителя
можно разбить на соответственные пары,
то получим, что вся сумма равна 0.
Свойство 4. Если все элементы, какой либо строки (столбца) матрицы умножить на скаляр , то на скаляр умножится и сам определитель.
Доказательство. Пусть - квадратная матрица порядка и - матрица, получающаяся из матрицы в результате умножения -ой строки на скаляр :
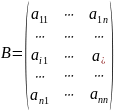 .
.
Тогда,
по определению определителя,
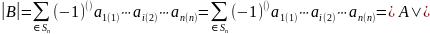 .
.
Следствие. Определитель матрицы, у которой какие-либо две строки (столбца) пропорциональны, равен нулю.
Свойство
5. Если каждый
элемент
-ой
строки матрицы
есть сумма
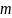 слагаемых, то определитель матрицы
равен сумме m
определителей, причем в матрице первого
определителя в
-ой
строке (
-ом
столбце) стоят первые слагаемые, в
матрице второго – вторые и т.д., а
остальные строки те же, что и в матрице
.
слагаемых, то определитель матрицы
равен сумме m
определителей, причем в матрице первого
определителя в
-ой
строке (
-ом
столбце) стоят первые слагаемые, в
матрице второго – вторые и т.д., а
остальные строки те же, что и в матрице
.
Доказательство.
Предположим, что каждый элемент
-ой
строки матрицы
есть сумма
слагаемых:
 .
Тогда
.
Тогда
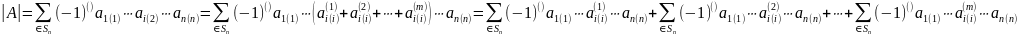 .
Каждая из полученных
сумм является определителем, описанным
в условии свойства.
.
Каждая из полученных
сумм является определителем, описанным
в условии свойства.
Свойство 6. Если к какому-нибудь столбцу (строке) матрицы определителя прибавить другой столбец (строку) матрицы, умноженный на произвольный скаляр, то определитель матрицы не изменится.
Доказательство.
Запишем квадратную матрицу
в виде
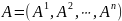 .
Предположим, что матрица
получается из матрицы
в результате прибавления к первому
столбцу
-го
столбца, умноженного на скаляр
,
т.е.
.
Предположим, что матрица
получается из матрицы
в результате прибавления к первому
столбцу
-го
столбца, умноженного на скаляр
,
т.е.
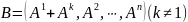 .
По свойству 5:
.
По свойству 5:
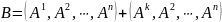 .
В этой сумме второй определитель равен
нулю. Следовательно,
.
В этой сумме второй определитель равен
нулю. Следовательно,
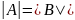 .
.
Следствие. Если к какому-нибудь столбцу (строке) матрицы определителя прибавить линейную комбинацию других столбцов (строк) матрицы, то определитель матрицы не изменится.
Свойство 7. Если какой-нибудь столбец (строка) квадратной матрицы есть линейная комбинация других столбцов (строк) матрицы, то определитель матрицы равен нулю.
Миноры и алгебраические дополнения.
(Лекция 22.)
Определение. Минором -го порядка квадратной матрицы , называется определитель матрицы, получающейся из матрицы и содержащий строк и столбцов.
Минорами первого порядка матрицы являются ее элементы.
Определение.
Определитель матрицы, полученной из
квадратной матрицы
вычеркиванием
-ой
строки и
-го
столбца, называется минором
элемента
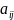 и обозначается через
и обозначается через
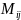 .
.
Определение.
Если из всех слагаемых определителя
выбрать только те, которые содержат
элемент
,
и вынести его за скобку то сумма,
полученная в скобках называется
алгебраическим
дополнением элемента
,
и обозначается через
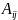 .
.
Теорема.
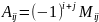 .
.
Доказательство.
Из всех слагаемых определителя выберем
только те, которые содержат элемент
,
и вынесем его за скобку, получим
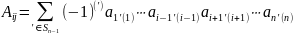 ,
определим, как связаны соответствующие
подстановки
и
,
определим, как связаны соответствующие
подстановки
и
 ,
если
- подстановка, содержащая отображение
,
если
- подстановка, содержащая отображение
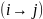 ,
а
- подстановка, полученная из
удалением отображения
.
Для этого определим, сколько инверсий
теряет подстановка
.
Пусть
символов, находящихся перед символом
образуют с ним инверсию, т.е. из
,
а
- подстановка, полученная из
удалением отображения
.
Для этого определим, сколько инверсий
теряет подстановка
.
Пусть
символов, находящихся перед символом
образуют с ним инверсию, т.е. из
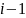 символа, находящихся перед символом
-
символов больше чем
.
Следовательно,
символа, находящихся перед символом
-
символов больше чем
.
Следовательно,
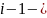 символов перед
- меньше
.
Так как всего символов меньших, чем
-
символов перед
- меньше
.
Так как всего символов меньших, чем
-
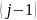 ,
то оставшиеся
,
то оставшиеся
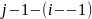 символов меньших, чем
,
будут справа от
,
и значит образовывать с ним инверсии.
Таким образом, символ
дает
символов меньших, чем
,
будут справа от
,
и значит образовывать с ним инверсии.
Таким образом, символ
дает
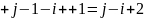 инверсий. И значит,
инверсий. И значит,
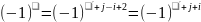 .
.
В
итоге получим,
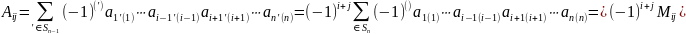 .
.
Следствие.
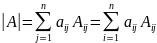 - разложение определителя по строке
(столбцу).
- разложение определителя по строке
(столбцу).
