
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«УФИМСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЯНОЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ».
Кафедра математики Реферат
На тему:
«Частные производные. Полный дифференциал, его связь с частными производными. Применение полного дифференциала к приближенным вычислениям.»
Выполнил: ст.гр.ПБ-10-01 Фаизов В.Р.
Проверил: доцент Абзалимов Р.Р.
Уфа 2011г.
ОГЛАВЛЕНИЕ
Часть №1 4
Часть №2 13
Часть №3 16
Список литературы. 18
Часть №1
Частные производные. Полный дифференциал, его связь с частными производными. Применение полного дифференциала к приближенным вычислениям.
Частные производные первого порядка функции двух переменных
Пусть функция
 определена в некоторой окрестности
точки
определена в некоторой окрестности
точки
 .
.


Рис. 1
Дадим аргументу
x0
произвольное ненулевое приращение
 ,
оставляя значение аргумента y0
неизменным, т.е. перейдем на плоскости
(xOy)
от точки
к точке
,
оставляя значение аргумента y0
неизменным, т.е. перейдем на плоскости
(xOy)
от точки
к точке
 (см. рис. 1). Тогда соответствующее
приращение функции
(см. рис. 1). Тогда соответствующее
приращение функции

называется частным приращением функции по переменной x в точке М.
Дадим аргументу
y0
произвольное ненулевое приращение
 ,
оставляя значение аргумента x0
фиксированным, т.е. перейдем на плоскости
(xOy)
от точки
к точке
,
оставляя значение аргумента x0
фиксированным, т.е. перейдем на плоскости
(xOy)
от точки
к точке
 .
Тогда соответствующее приращение
функции
.
Тогда соответствующее приращение
функции


называется частным приращением функции по переменной y в точке М.
Дадим аргументу
x0
приращение
,
а аргументу y0
– приращение
,
т.е. перейдем на плоскости (xOy)
от точки
 к точке
к точке
 .
Тогда соответствующее приращение
функции
.
Тогда соответствующее приращение
функции

называется полным приращением функции в точке М.
Частной
производной функции
 в точке
по переменной x
называется предел отношения частного
приращения
в точке
по переменной x
называется предел отношения частного
приращения
 к приращению
при стремлении
к нулю (если этот предел существует).
Обозначается частная производная так:
к приращению
при стремлении
к нулю (если этот предел существует).
Обозначается частная производная так:
 .
По определению
.
По определению
 .
.
Из определения
следует, что частная производная функции
двух переменных по переменной
 представляет собой обыкновенную
производную функции одной переменной
при
фиксированном значении переменной
представляет собой обыкновенную
производную функции одной переменной
при
фиксированном значении переменной
 .
.
Геометрически
частная производная по
функции двух переменных
в точке
есть тангенс
угла, который образует касательная
прямая, проведенная в точке к линии пересечения поверхности
с плоскостью
к линии пересечения поверхности
с плоскостью
 ,
с положительным направлением оси
,
с положительным направлением оси
 ,
т.е.
,
т.е.
 (см. рис. 3). Приращение аппликаты (третьей
координаты) этой касательной,
соответствующее приращению
аргумента
при фиксированном значении аргумента
,
(по аналогии с функцией одной переменной)
называют частным
дифференциалом функции двух переменных
по переменной
и обозначают
(см. рис. 3). Приращение аппликаты (третьей
координаты) этой касательной,
соответствующее приращению
аргумента
при фиксированном значении аргумента
,
(по аналогии с функцией одной переменной)
называют частным
дифференциалом функции двух переменных
по переменной
и обозначают
 .
При этом
.
При этом
 (см. рис.3). Поскольку под
дифференциалом аргумента понимают
приращение этого аргумента (т.е.
(см. рис.3). Поскольку под
дифференциалом аргумента понимают
приращение этого аргумента (т.е.
 ),
то
),
то
 .
.
Аналогично
определяется частная
производная
 функции
по переменной
в точке М
и частный
дифференциал
функции
по переменной
в точке М
и частный
дифференциал
 .
.
Другие обозначения
такой производной:
 .
.
Частные производные
вычисляют по формулам и правилам
вычисления производных функций одной
переменной, но
при этом для нахождения производной
 надо считать y
постоянной величиной, а для нахождения
надо считать y
постоянной величиной, а для нахождения
 надо считать x
постоянной величиной (константой).
надо считать x
постоянной величиной (константой).
Справедливы следующие правила:
Пример
1. Дана функция
двух переменных:
 .
Найти частные производные этой функции
по x
и y,
вычислить значения найденных частных
производных в точке А(-2;1).
.
Найти частные производные этой функции
по x
и y,
вычислить значения найденных частных
производных в точке А(-2;1).

Считая y постоянной величиной, найдем (подчеркнем все постоянные величины):

Найдем значение этой производной в точке А(-2;1):
 .
.
Считая x постоянной величиной, найдем (подчеркнем все постоянные величины):

 .
.
Пусть
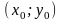 -
точка, в которой у функции
существует частная производная
-
точка, в которой у функции
существует частная производная
 (то есть значение этой производной в
точке
можно
вычислить). Тогда частная производная
имеет следующий смысл: если
значение переменной
зафиксировать
и не изменять, а значение переменной x
увеличивать, то
(то есть значение этой производной в
точке
можно
вычислить). Тогда частная производная
имеет следующий смысл: если
значение переменной
зафиксировать
и не изменять, а значение переменной x
увеличивать, то

Таким образом, частная производная характеризует скорость изменения функции в положительном направлении оси .
Аналогичный смысл
имеет частная производная
 (в этом случае значение
(в этом случае значение
 фиксируется, а переменная y
увеличивается).
фиксируется, а переменная y
увеличивается).
Дифференциал функции. Касательная плоскость.
Касательная
плоскость
в точке
K(x0,y0,z0)
к графику функции
– это плоскость, в которой расположены
все касательные прямые к линиям на
поверхности
,
проходящим через точку K
(на рис. 5
плоскость
 является касательной к поверхности
в
точке K).
является касательной к поверхности
в
точке K).

Рис. 2.
Дифференциалом
функции
называют
приращение координаты
касательной плоскости в
точке
 к поверхности, заданной уравнением
,
соответствующее приращениям
и
аргументов
функции. Дифференциал функции
обозначается
к поверхности, заданной уравнением
,
соответствующее приращениям
и
аргументов
функции. Дифференциал функции
обозначается
 .
На рисунке 2 показано, что
.
На рисунке 2 показано, что
 или
или
 .
.
Пусть
 - произвольная точка плоскости, касательной
к поверхности
в
точке
.
Поскольку
- произвольная точка плоскости, касательной
к поверхности
в
точке
.
Поскольку
 ,
,
 ,
,
 ,
из выражения для дифференциала получаем
уравнение касательной плоскости:
,
из выражения для дифференциала получаем
уравнение касательной плоскости:
 .
.

Теорема:
(Необходимое
условие дифференцируемости функции).
Если функция
 дифференцируема в точке
дифференцируема в точке
 ,
то она непрерывна в этой точке, имеет в
ней частные производные
,
то она непрерывна в этой точке, имеет в
ней частные производные

Теорема:
(Достаточное
условие дифференцируемости функции).
Если функция
имеет непрерывные частные производные
 и
и
 в точке
,
то она дифференцируема в этой точке и
ее полный дифференциал выражается
формулой
в точке
,
то она дифференцируема в этой точке и
ее полный дифференциал выражается
формулой
 или
или

Отметим, что для
функции
 одной переменной существование
производной
одной переменной существование
производной
 в точке является необходимым и достаточным
условием ее дифференцируемости в этой
точке.
в точке является необходимым и достаточным
условием ее дифференцируемости в этой
точке.
Чтобы функция была дифференцируема в точке, необходимо, чтобы она имела в ней частные производные, и достаточно, чтобы она имела в точке непрерывные частные производные.
Пример 2.
Для функции
(см. пример 1) дифференциал в точке А(-2;1)
равен
 .
Вычислив значение функции
.
Вычислив значение функции
 ,
можно составить уравнение касательной
плоскости в точке А(-2;1)
к графику данной функции:
,
можно составить уравнение касательной
плоскости в точке А(-2;1)
к графику данной функции:
 или
или
 .
.
Полный дифференциал функции многих переменных
1.
 .
.
Опр. 1.
Функцию
 называют дифференцируемой во внутренней
точке
называют дифференцируемой во внутренней
точке
 ,
если приращение функции в этой точке
,
если приращение функции в этой точке
 можно представить
в следующем виде:
можно представить
в следующем виде:

где
 конечные
константы,
конечные
константы,
 (1)
(1)
Опр. 2.
Если
дифференцируема в
,
то главная линейная часть ее приращения
называется дифференциалом функции
в точке
и обозначается

Итак,
 (2)
(2)
Теорема
1. Если
дифференцируема в
,
то в этой точке существуют и конечны
все частные производные
 ,
причем они равны
,
причем они равны
 .
.
Таким образом,
если функция дифференцируема, то,
условившись приращения независимых
переменных обозначать
 и называть их дифференциалами, для
дифференциала функции согласно (2) и
теореме получаем:
и называть их дифференциалами, для
дифференциала функции согласно (2) и
теореме получаем:
 (3)
(3)
Дифференциал
применяется в приближенных вычислениях:
если функция
-
линейная, то приращение функции
 ,
если же функция
-
нелинейная, то
,
если же функция
-
нелинейная, то
 при малых
приращениях аргументов
и
.
при малых
приращениях аргументов
и
.
Пример 3.
Вычислить:
 .
.
Рассмотрим функцию
 .
Требуется найти значение этой функции
при x=1,02
и y=3,04.
Поскольку
.
Требуется найти значение этой функции
при x=1,02
и y=3,04.
Поскольку
 и
и
 ,
то выберем начальные значения аргументов
следующим образом:
,
то выберем начальные значения аргументов
следующим образом:
 и
и
 (при этом
(при этом

 )
и дадим аргументам малые приращения
)
и дадим аргументам малые приращения
 и
и
 .
Тогда
.
Тогда

 .
.
Найдем частные производные:
 ,
,
 .
.
Вычислим значения
частных производных в точке
,
то есть в точке (1; 3):
 ,
,
 .
Тогда
.
Тогда

 .
.




