3. Решение системы трех линейных алгебраических уравнений при помощи обратной матрицы

Присоединенной (союзной) матрицей к квадратной матрице

А= называется матрица

, (11)

где – алгебраические дополнения элементов определителя матрицы А.

Матрица называется обратной к квадратной матрице А, если выполнено условие: , где Е – единичная матрица той же размерности, что и А.

Обратная матрица существует тогда и только тогда, когда квадратная матрица А – невырожденная, т.е. .

Чтобы найти обратную матрицу , необходимо:

а) проверить невырожденность матрицы А, вычислив определитель detA;

б) найти союзную матрицу А^* к матрице А;

в) найти обратную матрицу по формуле:

. (12)

Если систему линейных алгебраических уравнений (8) переписать в матричном виде AX = B, то ее решение можно получить матричным способом, т.е. при помощи обратной матрицы:

, (13)

где – обратная матрица для данной матрицы А.

6. Решение системы линейных алгебраических уравнений методом Гаусса

Метод Гаусса для решения системы линейных алгебраических уравнений заключается в последовательном исключении неизвестных из уравнений системы. Рассмотрим его использование на примере системы четырех уравнений относительно четырех неизвестных:

(14)

Требуется найти решение системы (14): х₁, х₂ , х₃, х₄.

Решение системы линейных алгебраических уравнений методом Гаусса осуществляется в два этапа, которые называются «прямой» и «обратный» ход.

Прямой ход. Для удобства вычислений используем расширенную матрицу A|b, полученную присоединением к матрице А столбца свободных членов:

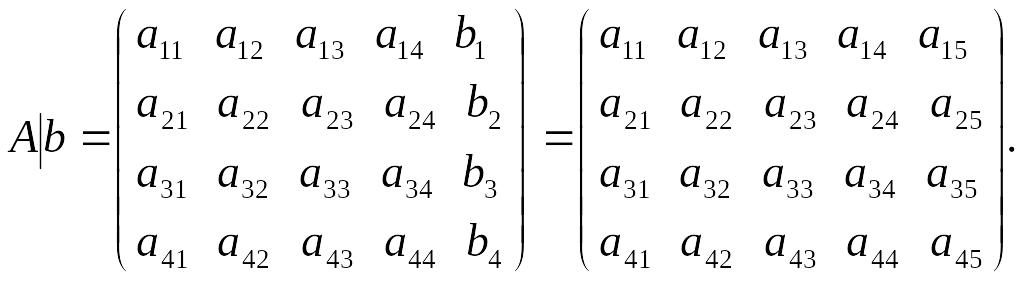(15)

Для k = 1, 2, 3 (где k – номер шага) осуществляется исключение неизвестной из уравнений с номерами i > k . Для этого выполняем следующие вычисления:

1) все элементы k -й строки расширенной матрицы делим на а_kk:

. (16)

Принято называть k-ю строку – ведущей строкой, а элемент а_kk – ведущим элементом k-го шага.

2) из всех строк расширенной матрицы с номерами i > k (т.е. строк, расположенных под ведущей строкой) вычитаем k-ю строку, умноженную на элемент а_ik, получая в расширенной матрице нули под ведущим элементом а_kk:

. (17)

Если матрица А коэффициентов при неизвестных в системе (14) – невырожденная, то в результате прямого хода за 3 шага система приводится к верхнему треугольному виду:

Полученная система равносильна исходной системе, т.е. имеет то же самое решение х₁, х₂ , х₃, х₄.

Обратный ход. Находим неизвестные х₄, х₃ , х₂, х₁ по формулам

(18)

Образцы решения задач

Задача 1. Даны многочлен f(x) и матрица А:

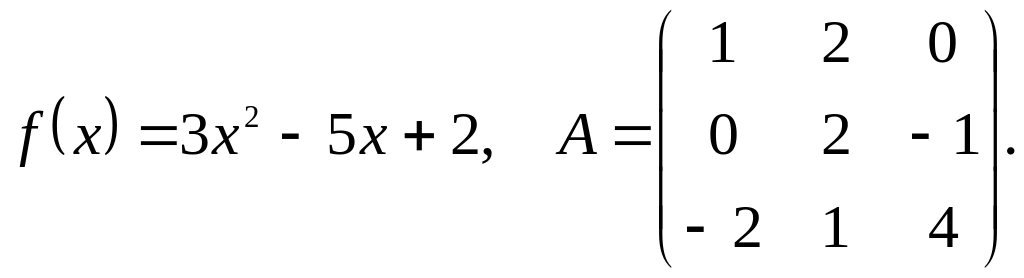
Требуется найти значение матричного многочлена f(A).

Задача 2. Дана система трех линейных алгебраических уравнений с тремя неизвестными:

Требуется:

1) записать систему в матричной форме;

2) найти решение системы с помощью формул Крамера;

3) решить систему при помощи обратной матрицы.

Задача 3. Дана система четырех линейных алгебраических уравнений с четырьмя неизвестными:

Требуется найти решение системы методом Гаусса и выполнить проверку.

Решение задачи 1. Записываем матричный многочлен: Здесь Е – единичная матрица той же размерности, что и А, т.е. 3-го порядка.

Найдем матрицу A². При умножении матрицы A на себя используем правило «строка на столбец» (формула (3)):

A² = A·A =

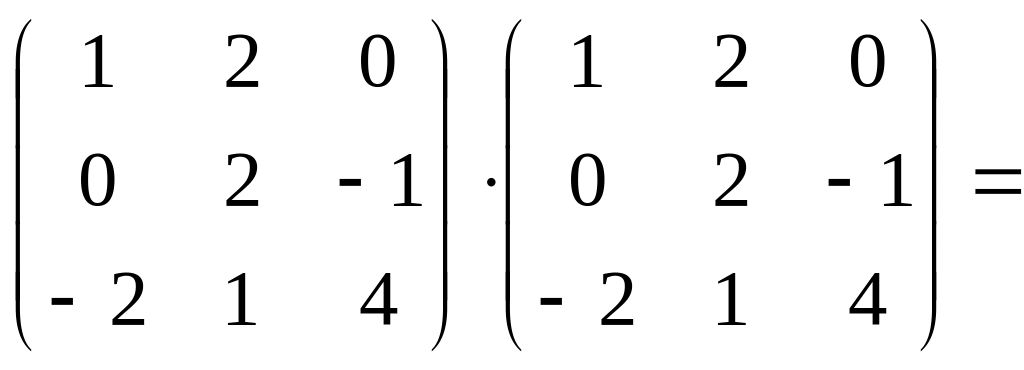
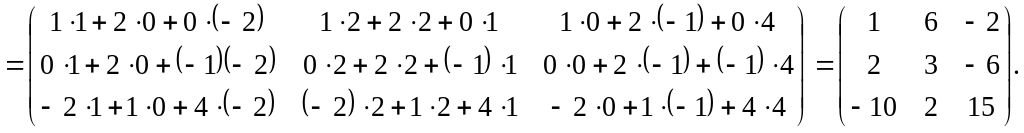
Найдем матрицу 2Е, используя правило умножения матрицы на число (формула (1)):

E =

Теперь найдем значение матричного многочлена f(A), используя правило умножения матрицы на число и правило сложения матриц (формула (2)):

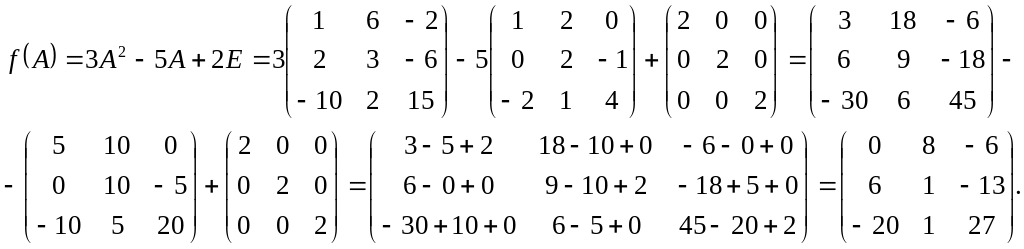
Ответ:

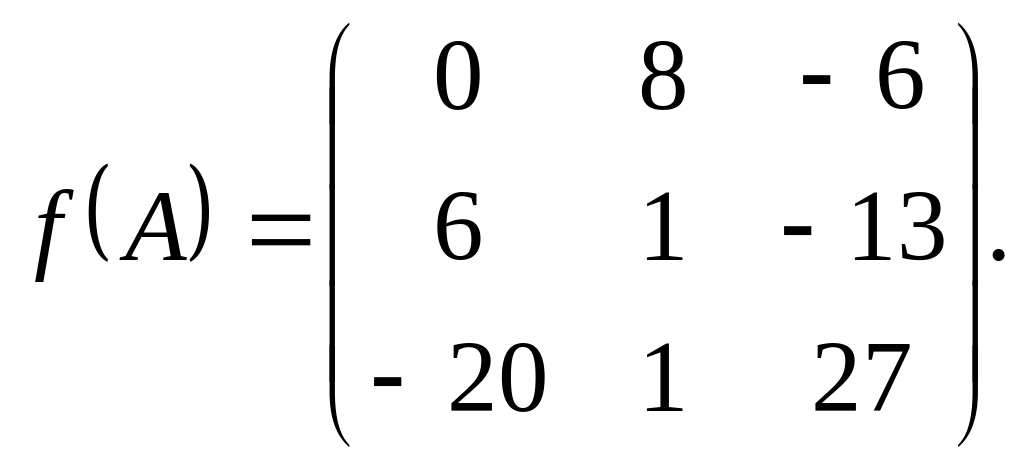
Решение задачи 2.

1. Запишем систему в матричной форме:

, или AX = B, где

(Во втором уравнении системы отсутствует неизвестная х₃, т.е. а₂₃ = 0).

2) Решим систему с помощью формул Крамера. Для этого по формулам (9) составляем главный определитель системы из коэффициентов при неизвестных в левых частях уравнений и три вспомогательных определителя:

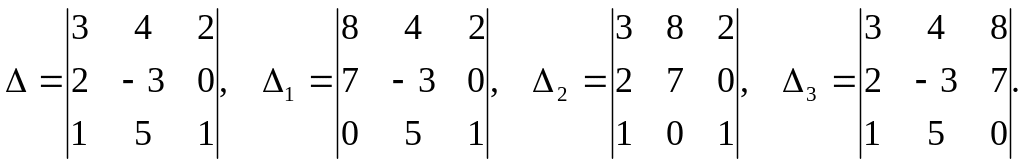
Вычислим эти определители, используя формулу (5):

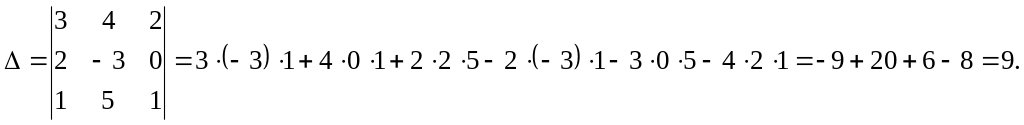
Так как ∆ ≠ 0, то данная система имеет единственное решение.

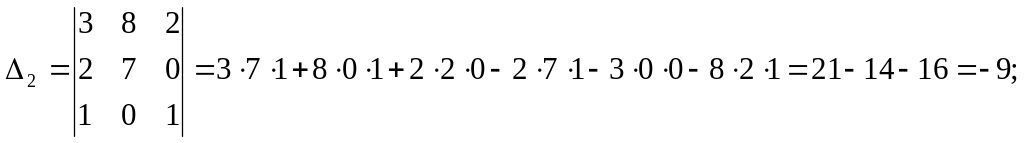
Найдем решение системы по формулам Крамера (10):

3) Решим систему при помощи обратной матрицы.

1. Определитель 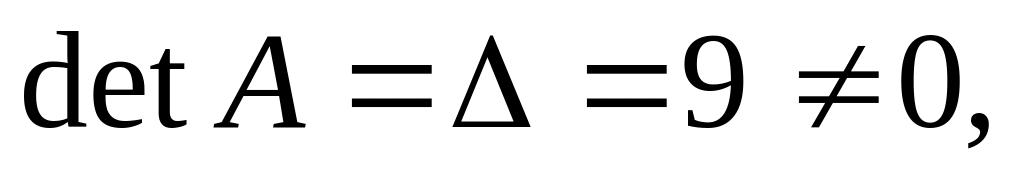следовательно, обратная матрица существует.

б) Чтобы найти союзную матрицу к матрице А, необходимо вычислить по формулам (6) алгебраические дополнения всех ее элементов:

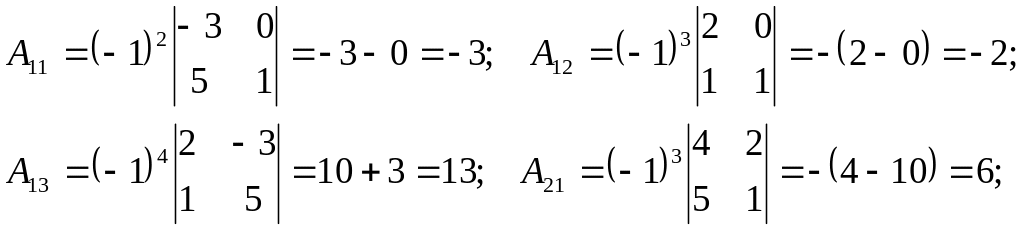
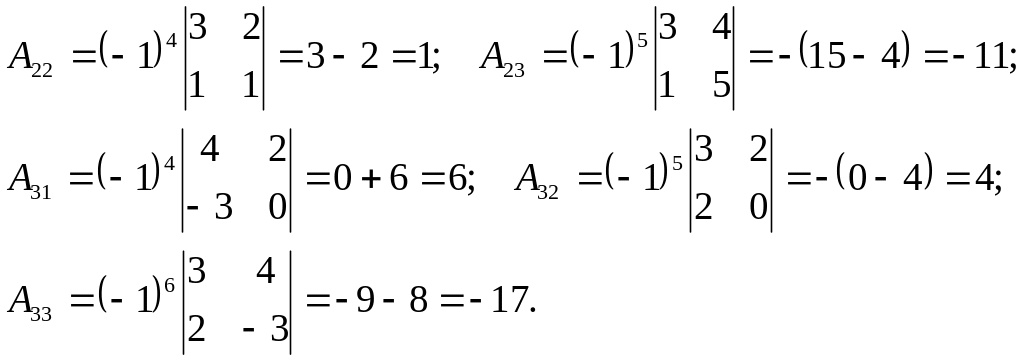
Здесь определители 2-го порядка вычислены по формуле (4).

Тогда союзная матрица (см. формулу (11)):

в) Найдем обратную матрицу по формуле (12):

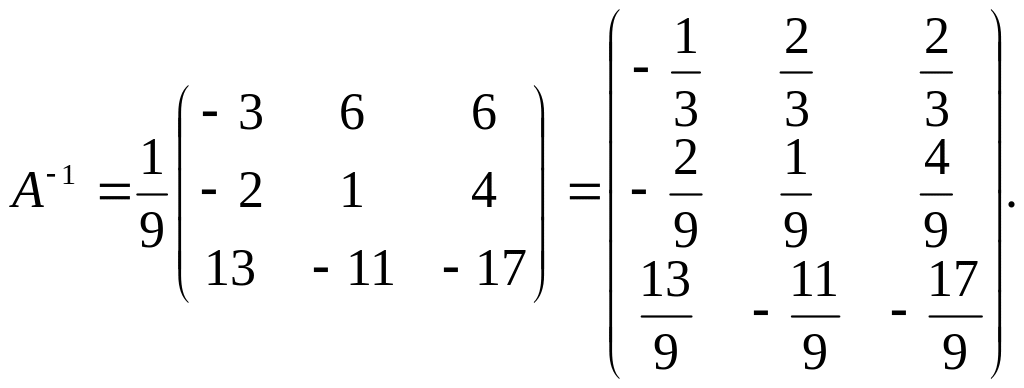
г) Получим решение системы при помощи обратной матрицы по формуле (13) (правило «строка на столбец»):

.

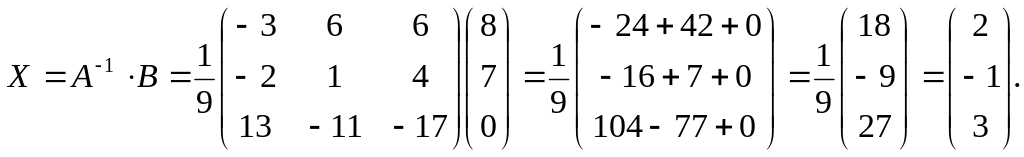
Решение, полученное матричным способом, совпадает с тем, что получено по формулам Крамера, что подтверждает правильность этого решения.

Ответы:

1) система в матричной форме: AX = B, где ;

2) решение системы, полученное с помощью формул Крамера:

;

3) решение системы, полученное при помощи обратной матрицы:

.

Решение задачи 3.

Прямой ход. Построим расширенную матрицу A|b путем присоединения к матрице А столбца свободных членов (формула (15)):

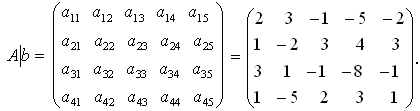
Приведение системы к верхнему треугольному виду осуществляем за 3 шага, используя формулы (16), (17).

1шаг (k = 1): исключаем неизвестную х₁ из уравнений с номерами i= 2, 3, 4.

1) Все элементы 1-й (ведущей) строки расширенной матрицы делим на ведущий элемент а₁₁=2, получаем строку:

.

2) Из 2-й строки вычитаем ведущую строку , умноженную на элемент а₂₁= 1, получаем: .

Из 3-й строки вычитаем ведущую строку , умноженную на элемент а₃₁= 3, получаем: .

Из 4-й строки вычитаем ведущую строку , умноженную на элемент а₄₁= 1, получаем: .

В результате 1-го шага произошло исключение неизвестной х₁ из 2-го, 3-го и 4-го уравнений системы, расширенная матрица и система теперь имеют вид:

(A|b)^′= ,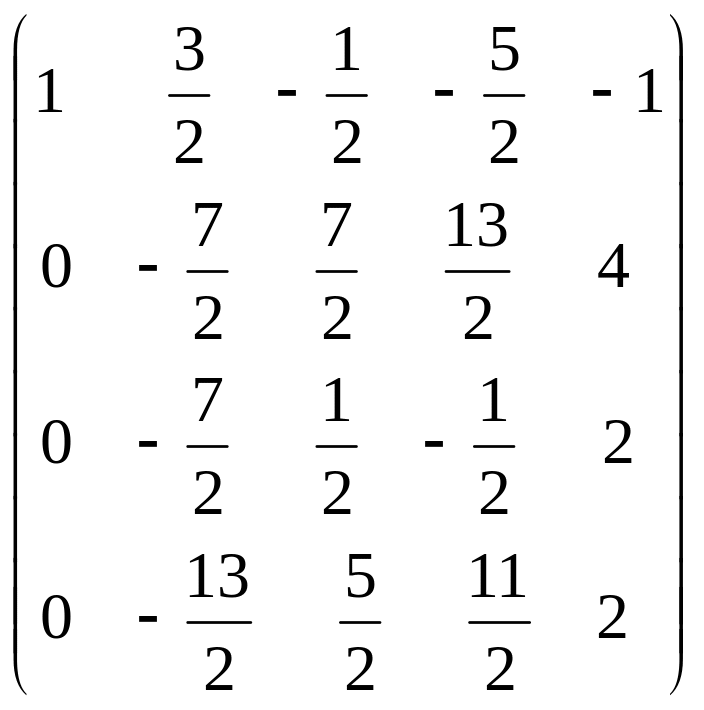

Далее работаем только с 2, 3, 4 строками расширенной матрицы (A|b)^′.

2шаг (k = 2): исключаем неизвестную х₂ из уравнений с номерами i= 3,4.

1) Все элементы 2-й (ведущей) строки делим на ведущий элемент , получаем строку: .

2) Из 3-й строки вычитаем ведущую строку , умноженную на элемент , получаем: .

Из 4-й строки вычитаем ведущую строку , умноженную на элемент , получаем: .

В результате 2-го шага произошло исключение неизвестной х₂ из 3-го и 4-го уравнений системы, расширенная матрица и система теперь имеют вид:

(A|b)′′= ,

Далее работаем только с 3, 4 строками расширенной матрицы (A|b)′′.

3шаг (k = 3): исключаем неизвестную х₃ из уравнения с номером i= 4.

1) Все элементы 3-й (ведущей) строки делим на ведущий элемент

= –3, получаем строку: .

2) Из 4-й строки вычитаем ведущую строку , умноженную на элемент = – 4, получаем: .

В результате 3-го шага произошло исключение неизвестной х₃ из 4-го уравнения системы, расширенная матрица и система теперь имеют вид:

(A|b)′′′= ,

Таким образом, в результате прямого хода получили систему с матрицей верхнего треугольного вида:

Преобразования прямого хода можно записать в кратком виде:

~ ~

~ ~

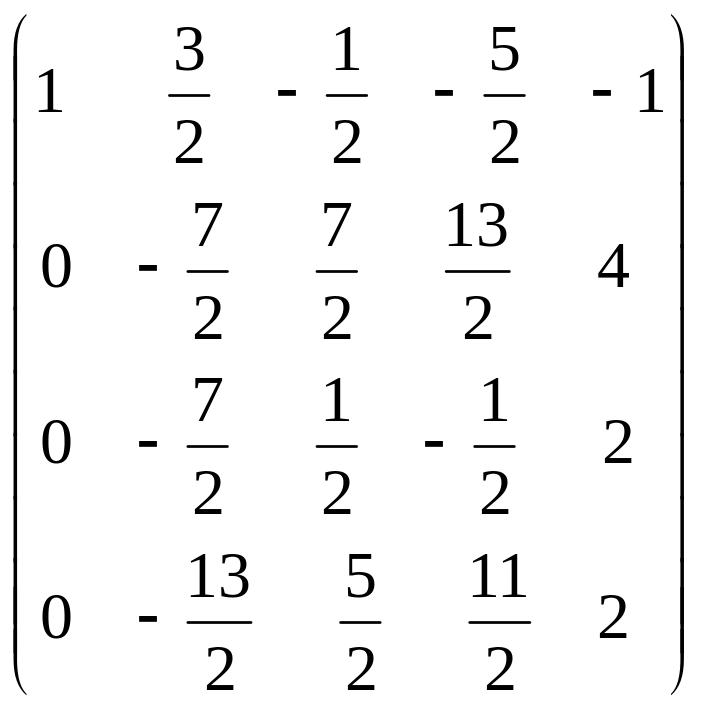Обратный ход. Находим неизвестные х₄, х₃ , х₂, х₁ по формулам (18).

Из 4-го уравнения находим:

из 3-го уравнения находим:

из 2-го:

из 1-го:

Получено решение системы: х₁= –2, х₂ = 0, х₃ = 3, х₄ = –1.

Проверка. Подставим найденные значения х₁, х₂ , х₃, х₄ во все уравнения системы:

Все уравнения системы после постановки обратились в тождества, значит, решение получено верно.

Ответ: х₁= –2, х₂ = 0, х₃ = 3, х₄ = –1.