Невырожденные кривые

Кривая второго порядка называется невырожденной, если Могут возникать следующие варианты:

Невырожденная кривая второго порядка называется центральной, если
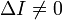
- эллипс — при условии D > 0 и ΔI < 0;
  - частный случай эллипса — окружность — при условии I² = 4D или a₁₁ = a₂₂,a₁₂ = 0;
- мнимый эллипс (ни одной вещественной точки) — при условии ΔI > 0;
- гипербола — при условии D < 0;
Невырожденная кривая второго порядка называется нецентральной, если ΔI = 0
- парабола — при условии D = 0.

[Править] Вырожденные кривые

Кривая второго порядка называется вырожденной, если Δ = 0. Могут возникать следующие варианты:

вещественная точка на пересечении двух мнимых прямых (вырожденный эллипс) — при условии D > 0;
пара вещественных пересекающихся прямых (вырожденная гипербола) — при условии D < 0;
вырожденная парабола — при условии D = 0:
- пара вещественных параллельных прямых — при условии B < 0;
- одна вещественная прямая (две слившиеся параллельные прямые) — при условии B = 0;
- пара мнимых параллельных прямых (ни одной вещественной точки) — при условии B > 0.

14; 15) определитель второго порядка есть число, равно

произведению элементов главной диагонали минус произведение

элементов побочной диагонали. Слагаемые a11 a22 и a12 a21 называются

членами определителя второго порядка. Такой же принцип можно использовать для определителя n-ого порядка.

Свойства определителей

1. Определитель матрицы, полученной из данной транспонирова-

нием, равен определителю данной матрицы: | А′ | =| А | .

Это свойство является прямым следствием теоремы 3.2(см по сыллки http://www.bseu.by/hm/uchm/Posobie/Posobie_1.pdf ) и утвер-

ждает, что все свойства, сформулированные для строк определителя,

будут справедливы и для его столбцов.

2. При перестановке местами двух строк, определитель меняет

знак на противоположный, сохраняя при этом свою абсолютную ве-

личину.

3. Определитель с двумя одинаковыми строками равен нулю.

4. Если все элементы некоторой строки определителя умножить

на одно и то же число, то сам определитель умножится на это число.

5. Если к элементам некоторой строки определителя прибавить

элементы другой строки, умноженные на произвольное число α, то

определитель не изменится.

16) Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. Хотя исторически рассматривались, например, треугольные матрицы, в настоящее время говорят исключительно о матрицах прямоугольной формы, так как они являются наиболее удобными и общими.

Матрицы широко применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. В этом случае, количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате решение систем линейных уравнений сводится к операциям над матрицами.

Матрицы: Мар А размерностью МхN называют набор чисел aij упорядоченных с помощью индексов i j где i=1 до m(номер строки) j=1 до n(номер столбца)

Операции:

Линейные операции: Сложение и умножение на скаляр по элеменнтно.

Aи В € М(m;n)=> С=А+В+|Сij| € M(m;n)

Транспортирование: замена строк на столбец 123 t равно 14

456 25

Умножение: строка на столбец – 1 2 3 умножить на 5 3 равно 1*5+2*6+3*7 1*3+2*2+3*4

3 2 1 6 2 3*5+2*6+1*7 3*3+2*2+1*4

7 4

17) Обратная матрица: Матрица называется обратной матрицей для квадратной матрицы , если Где E единичная матрица. Из определения следует, что обратная матрица будет квадратной матрицей того же порядка, что и матрица (иначе одно из произведений или было бы не определено). +++ В тетради