70

Лекция 8

Тема: ЭКСТРАПОЛЯЦИЯ ВРЕМЕННЫХ РЯДОВ

План лекции

1. Типы роста экономических процессов

2. Доверительные интервалы прогноза

3. Проверка адекватности выбранных моделей

4. Характеристики точности моделей

5. Упрощённые методы оценивания параметров нелинейных зависимостей

1. Одним из самых важных этапов при построении эконометрических прогнозных моделей является выбор вида функции. Обычно для решения этой задачи этап предварительной обработки данных исследуется механизм функционирования моделируемых процессов и уточняется их экономическая сущность. В процессе этих исследований пытаются выяснить:

1. является ли интересующий нас процесс монотонно возрастающим или убывающим, стабильным или взрывчатым, имеет ли экстремум (экстремумы), наблюдаются ли в его развитии сезонные явления;

2. ограничен ли сверху (снизу) каким-либо пределом, имеет ли асимптоты;

3. есть ли у функции, описывающей этот процесс, точки перегиба;

4. обладает ли она (функция) свойством симметрии;

5. имеет ли процесс явное ограничение своего развития во времени.

Если удается в результате этих исследований выявить какие-либо свойства моделируемого процесса, то этими свойствами стараются наделить функцию, которая выбирается в качестве тренда (основной закономерности). Такой подход позволяет строить содержательно интерпретируемые модели, обеспечивающие более высокую достоверность прогнозных оценок, чем формально построенные.

Отметим, что строгих предписаний по поводу последовательности действий при построении прогнозных эконометрических моделей нет. У исследователя есть достаточно свободы при решении многих вопросов, поэтому всегда нужно помнить, что процесс построения модели – это не только наука, но и искусство.

Несмотря на сделанное замечание, в дальнейшем изложении будем придерживаться вполне определенной схемы выбора функции тренда, предусматривающей следующие действия:

1. сглаживание данных временного ряда (необязательно);

2. расчет абсолютных приростов;

3. определения типа роста путем анализ приростов или их производных характеристик;

4. уточнения типа роста с помощью содержательного анализа;

5. выбор из класса функций, описывающих данный тип роста, наилучшей.

Анализ приростов и их производных характеристик позволяет определить характер динамики прогнозируемого процесса (тип роста). Каждый тип роста описывается соответствующими функциями. Опишем эти типы роста.

1.1. Постоянный рост. Он характеризуется постоянными или мало изменяющимися абсолютными приростами. Следовательно, если после сглаживания временного ряда окажется, что вычисленные приросты примерно одинаковы для всех t, то есть полное основание строить модель, которая описывает этот тип роста. В качестве такой модели принято использовать линейную функцию

. (1.1)

Здесь

- теоретический (расчетный) уровень базисного года;

- постоянный (ежегодный, ежемесячный) абсолютный прирост, равный первой производной.

. (1.2)

Темп прироста

(1.3)

для линейной функции монотонно убывает при .

1.2. Увеличивающийся рост. Для этого типа роста абсолютные приросты сглаженного ряда либо линейно растут, либо темпы прироста остаются почти неизменными. В первом случае мы имеем дело с параболической зависимостью

, (1.4)

у которой , а предельная величина абсолютного прироста изменяется линейно

. (1.5)

Во втором случае процесс описывается экспонентой

(1.6)

при .

Темп предельного прироста определяется выражением

. (1.7)

1.3. Уменьшающийся рост. В этом случае прирост сглаженного ряда уменьшается по линейному или какому-либо другому закону. В качестве тренда такого процесса может быть выбрана любая из следующих кривых:

Линейная логарифмическая

. (1.8)

Для нее величина абсолютного прироста в точке t

(1.9)

при убывает.

Степенная зависимость

(1.10)

при .

Абсолютный прирост

(1.11)

убывает при .

Может использоваться также парабола (1.4), но с отрицательным коэффициентом , так как для нее абсолютный прирост (1.5) является убывающей функцией t.

Часто для моделирования процессов этого типа применяют гиперболу вида

, (1.12)

для которой абсолютный прирост – убывающая функция

(1.13)

и для которой существует предел сверху

.

Встречаются также случаи, когда высокая точность аппроксимации достигается при использовании модифицированной экспоненты

. (1.14)

Модифицированная экспонента, как и гипербола, характеризуется быстро убывающим абсолютным приростом и наличием асимптоты

,

ограничивающий рост сверху.

1.4. Рост с качественным изменением динамических характеристик. При моделировании этого типа процесса применяются точки перегиба, т.е. точки, в которых вторая производная равна нулю. В случае, если увеличивающийся рост сменяется уменьшающимся ростом, то в качестве модели можно выбрать логарифмическую параболу

(1.15)

с или многочлен третьей степени

(1.16)

с .

К этому классу функций относятся также кривая Гомперца и кривая Перла-Рида (логистическая кривая). Уравнение кривой Гомперца имеет вид

. (1.17)

Логистическая кривая задается уравнением

. (1.18)

Параметры всех кривых, кроме двух последних, оцениваются с помощью метода наименьших квадратов. Метод построения кривых Гомперца и Перла-Рида будет рассмотрен ниже.

После определения типа роста рекомендуется для его уточнения провести содержательный анализ, смысл которого можно проиллюстрировать следующим примером.

Пусть анализ приростов на ретроспективном участке показал, что ряд динамики должен быть отнесен к процессам, которые характеризуются увеличивающимся ростом. Такой процесс, как было показано выше, хорошо описывается с помощью экспоненциальной кривой. Однако, первая половина логистической кривой также представлена экспонентой. Поэтому остановить свой выбор на увеличивающемся росте можно только в том случае, когда удастся обосновать гипотезу об экспоненциальной тенденции ряда в будущем. Гипотеза об экспоненциальной тенденции принимается в том случае, когда в результате содержательного анализа устанавливается, что исследуемый процесс в будущем не достигает состояния «насыщения».

Этап определения типа роста позволяет только ограничить число функций, приемлемых для описания данного временного ряда, сокращая число возможных вариантов, но, кроме линейного случая, не дает однозначного ответа. Окончательный выбор функции тренда осуществляется следующим образом. С помощью метода наименьших квадратов строятся все функции из того ограниченного набора, который определен для установленного типа роста. Из построенных функций в качестве тренда выбирается та, которая дает наименьшую среднюю квадратическую ошибку

, (1.19)

где

- фактические значения временного ряда;

- расчетные значения временного ряда;

- длина временного ряда.

В предположении, что в перспективном периоде тенденции ретроспективного периода сохраняются, с помощью так определенной функции рассчитываются прогнозные значения. Расчет осуществляется путем подстановки в уравнение кривой значений времени t, соответствующих периоду упреждения.

2. Рассчитанные по уравнению тренда принято называть точечными, так как для каждого момента времени определяется только одно значение прогнозируемого показателя. Вероятность того, что реальное значение в будущем совпадет с прогнозной оценкой невелика. Поэтому в дополнение к точечному прогнозу определяют границы возможного изменения прогнозируемого показателя, т.е., фактически, вычисляют интервальный прогноз. Несовпадение фактических значений с точечным прогнозом может быть вызвано:

1. субъективной ошибкой при выборе вида кривой;

2. погрешностью оценивания параметров кривых;

3. погрешностью, связанной с отклонением отдельных наблюдений от кривой тренда.

Погрешность, порождаемая вторым и третьим источником, может быть отражена в виде доверительного интервала прогнозного значения

, (2.1)

где

-точечный прогноз на момент t+l;

- значение t-статистики Стьюдента;

- средняя квадратическая ошибка прогноза;

n - длина временного ряда;

l - период упреждения.

Для линейной модели тренда (1.1) дисперсия может быть представлена в виде

, (2.2)

где

-дисперсия отклонений фактических наблюдений от расчетных;

- время упреждения, для которого делается экстраполяция, = n+l;

t - порядковый номер уровней ряда, t=1, 2, … , n;

- порядковый номер уровня, стоящего в середине ряда.

Используя формулу (2.2) доверительный интервал можно представить в виде

. (2.3)

Доверительные интервалы прогнозов, полученные с использованием нелинейных моделей (экспоненциальной, степенной и т.д.), определяются аналогичным образом. Отличие состоит только в том, что как при вычислении параметров кривой, так и при вычислении средней квадратической ошибки используются преобразованные значения уровней временного ряда (например, логарифмы и т.п.).

3. Проверка адекватности трендовых моделей реальному процессу строится на основе анализа случайной компоненты. В расчетах случайная компонента заменяется остатками, представляющими собой разность фактических и расчетных значений

. (3.1)

Принято считать, что модель адекватна описываемому процессу, если значения остаточной компоненты удовлетворяют свойствам случайности, независимости и подчиняются нормальному закону распределения.

При правильном выборе тренда отклонения от него будут носить случайный характер. В случае, если вид функции выбран неудачно, то последовательные значения остатков могут не обладать свойством независимости, т.е. они могут коррелировать между собой. В этом случае говорят, что имеет место автокорреляция ошибок.

Существует несколько приемов обнаружения автокорреляции. Наиболее распространенным является метод Дарбина-Уотсона. Этот критерий связан с гипотезой о существовании автокорреляции первого порядка. Его значения определяются по формуле

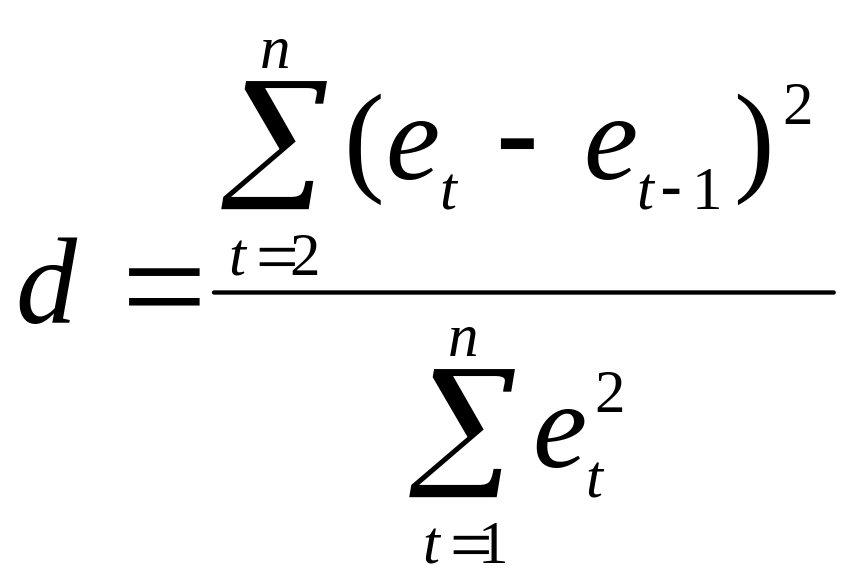. (3.2)

Смысл критерия становится очевидным при рассмотрении приближенного представления величины d

, (3.3)

где - коэффициент автокорреляции первого порядка (т.е. парный коэффициент корреляции между двумя рядами и ). Если в значениях имеется сильная положительная автокорреляция ( ), то величина d=0, в случае сильной отрицательной автокорреляции ( ) d=4. При отсутствии автокорреляции ( )d=2.

Для данного критерия найдены критические границы ( - нижняя, - верхняя), позволяющие принять или отвергнуть гипотезу. При сравнении величины d с нижней и верхней границами возможны следующие варианты:

1. Если , то гипотеза о независимости случайных отклонений (отсутствие автокорреляции) отвергается;

2. Если , то гипотеза о независимости случайных отклонений не отвергается;

3. Если , то нет достаточных оснований для принятия решений.

Рассмотренные варианты относятся к случаю, когда в остатках наблюдается положительная автокорреляция. Для проверки отрицательной автокорреляции с критическими значениями и сравнивается не сам коэффициент d, а 4-d.

4. Важнейшими характеристиками качества прогнозной модели являются показатели ее точности. Показатели рассчитываются на основе ошибок прогноза. Ошибка прогноза – величина, характеризующая расхождение между фактическим и расчетным показателем. Она определяется по формуле

, (4.1)

где

- фактическое значение показателя;

- прогнозное значение показателя.

Наряду с ошибками (4.1) широко используются относительные ошибки прогноза, выраженные в процентах относительно фактических значений показателей

. (4.2)

О точности модели нельзя сформировать правильное представление по отдельным прогнозным ошибкам, поэтому кроме мгновенных характеристик (ошибка, относительная ошибка), используются средние характеристики по модулю (абсолютные, относительные)

, (4.3)

. (4.4)

При проведении сравнительной оценки моделей может также использоваться среднеквадратическая ошибка прогноза

. (4.5)

Если приведенные характеристики вычисляются для перспективного периода, то их вычисление возможно только в том случае, когда станут известны фактические значения этого периода.

Иногда в качестве меры качества прогнозной модели может стать - относительное число случае, когда фактическое значение охватывалось интервальным прогнозом

, (4.6)

где

p – число прогнозов, подтвержденных фактическими данными;

q – число прогнозов, не подтвержденных фактическими данными.

В случае, когда все прогнозы подтверждаются (q=0), то =1.

Если ни один прогноз не подтверждается (р=0), то =0.

Коэффициент можно использовать для сопоставления по точности разных прогнозных моделей. Такое сопоставление корректно при условии, что для всех сопоставляемых моделей доверительные вероятности приняты одинаковыми.

5. Нелинейные зависимости типа кривой Гомперца, модифицированной экспоненты и некоторых видов логистических кривых нельзя привести к линейному виду путем элементарных преобразований, а, следовательно, невозможно воспользоваться методом наименьших квадратов для оценки параметров этих функций. Однако можно воспользоваться упрощенными методами оценивания параметров нелинейных кривых. Одним из таких методов является метод трех сумм.

Рассмотрим применение этого метода для различных типов кривых.

5.1. Метод трёх сумм для модифицированной экспоненты. Сначала рассмотрим метод трёх сумм применительно к модифицированной экспоненте

.

В соответствии с этим методом весь ряд наблюдений

, где N=3*n,

разбивается на три равных отрезка или периода по n уровней. Обозначим сумму уровней для каждого периода как .

Если бы уровни ряда точно следовали модифицированной экспоненте, т.е.

,

,

……………..,

,

то сумма этих уровней для первого подпериода составила бы величину

. (5.1.1)

Прежде чем перейдём к определению , упростим выражение (5.1.1). Нетрудно понять, что сумма в скобках – это геометрическая прогрессия со знаменателем b. Поэтому

, .

Откуда получаем, что

. (5.1.2)

Аналогично определим две следующие суммы:

, (5.1.3)

. (5.1.4)

Решение системы из 3-х уравнений (5.1.2)-(5.1.4) определяет три искомых параметра. Это решение получается в предположении, что суммы уровней расчётного ряда равны суммам уровней фактического ряда.

Для получения решения вычтем первое уравнение из второго и второе из третьего. Получаем

, (5.1.5)

. (5.1.6)

Решим эту систему относительно b, для чего разделим (5.1.6) на (5.1.5), в итоге получим:

,

а, следовательно,

. (5.1.7)

Подставляя в (5.1.5) найдём

. (5.1.8)

И, наконец, из уравнения (5.1.2) найдём k

. (5.1.9)

Таким образом, определены все параметры модифицированной экспоненты.

Замечание: Метод очень чувствителен к колебаниям исходных данных. Разность сумм в знаменателе при вычислении может оказаться равной нулю или быть отрицательной, и тогда нельзя определить. Поэтому перед расчётом параметров данные необходимо подвергнуть сглаживанию.

5.2. Метод трёх сумм для кривой Гомперца. Кривая Гомперца имеет вид

.