2. Інтерполяція кубічними сплайнами.

Кубічний сплайн – математична модель абсолютно гнучкого, пружного тонкого стержня. Якщо стержень закріпити в двох його кінцях з заданими кутами нахилу і , то стержень прийме форму, що мінімізує його потенціальну енергію. Нехай рівняння стержня визначається функцією . Умова рівноваги сплайна визначається рівнянням:

Цій умові задовольняє алгебраїчний многочлен третього степеня. Запишемо рівняння кубічного сплайна для відрізку

Якщо задана послідовність вузлів , то ми повинні знайти значень коефіцієнтів сплайнів, так як для кожного відрізу ми матимемо інше рівняння сплайну. Першу групу рівнянь ми отримаємо з умови, що наші сплайни проходять через задану сукупність вузлів:

- з умови знаходимо, що для

- з умови знаходимо , що

для .

Наступну групу рівнянь отримаємо з умови гладкості наших сплайнів. Для цього задамо умову неперервності перших і других похідних у вузлах:

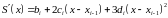
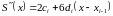
Отримаємо

для

для

Ми отримали систему 4n – 2 рівнянь. Ще два рівняння ми отримаємо з умов, що накладаються у крайніх вузлах. Задамо кривизну сплайна в крайніх вузлах рівною нулю, що відповідає випадку вільного кубічного сплайну:

,

Отримаємо, що та

Перейдемо до розв’язку отриманої системи. Послідовно знаходимо:

;

;

;

З рівняння

;

отримаємо вирази для коефіцієнтів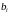

;

.

Запишемо систему рівнянь відносно коефіцієнтів c_i. Підставимо вирази для b_i та d_i в рівняння в рівняння умови неперервності перших похідних. Отримаємо рівняння:

Змінимо на одиницю індекс :

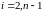
Використовуючи умови в 0-му та n-му вузлах, знаходимо

Система рівнянь для c_i має т.зв. трьох діагональну матрицю і для її розв’язку ми можемо використати метод прогонки.

3.) Інтерполяційні многочлени Лагранжа.

Побудуємо інтерполяційний многочлен для всього відрізку [x₀,x_n] виходячи з умови рівності значень цього многочлена у вузлах х_і, значенням заданої функції y_i.

Шукатимемо многочлен у вигляді лінійної комбінації многочленів степені n.

(1)

Задамо умову, щоб кожен многочлен l_i(x) перетворювався в нуль у всіх вузлах інтерполяції, крім і-го, де він повинен бути рівним 1.

Легко перевірити, що даним умовам відповідає многочлен виду:

(2)

З умови нормування знаходимо коефіцієнти с₀:

(3)

Аналогічно отримаємо:

(4)

Підставляючи (1) в (2) і (4) отримаємо:

Ця формула є інтерполяційним многочленом Лагран-жа.

Можна показати, що залишковий член який визначає похибку інтерполяції рівний:

де х^* Є [x₀…x_n]

4). Розділені різниці.

Введемо розділені різниці, які задовольняють такі рекурентні співвідношення. Розділена різниця нульового порядку співпадає зі значенням функції

.

Розділена різниця першого порядку

.

Розділена різниця другого порядку

.

В загальному ми можемо записати рекурентну формулу для обчислення розділених різниць k-го порядку через розділені різниці (k-1) порядку:

.

Можна показати, що

.

Розділена різниця є симетричною функцією своїх аргументів. Тобто вона

не міняється при будь-якій їх перестановці.

5). Скінченні різниці.

Введемо поняття скінченних різниць. Різницю називають скінченною різницею вперед, -скінченною різницею назад.

Скінченні різниці вищих порядків можна обчислити за допомогою рекурентних формул:

,

.

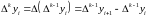Розглянемо їх основні властивості

- оператор скінченної різниці є лінійним

,

.

- між скінченними різницями вперед і назад є співвідношення

.

- скінченну різницю довільного порядку можна обчислити за формулою ,

де – коефіцієнт бінома Ньютона.

- скінченна різниця n-го порядку від многочлену степені n є константа , а різниці вищих порядків рівні нулю.

- у випадку рівновіддалених вузлів розділенгі різниці можна виразити через скінченні різниці

6). Вивід формули інтерполяційного многочлена Ньютона.

Многочлен Ньютона будемо шукати у вигляді:

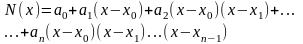(5)

Розглянемо випадок рівновіддалених вузлів.

Многочлен повинен проходити через задані вузли N(x_i)=y_i (i=0,1,2,…n). З цієї умови знаходимо коефіцієнти многочлена.

Аналогічно знаходимо інші коефіцієнти:

k=0,1,2,…,n

Підставляючи ці вирази у формулу (5) отримаємо:

Введемо заміну змінних:

x=х₀+th; t=(x-x₀)/h;

(x-x₁)/h=t-1; (x-x₂)h=t-2;

В цих позначеннях кінцево отримаємо вираз для першого інтерполяційного многочлена Ньютона.

Для покращення тотожності інтерполяції бажано щоби значення t було невелике.

Залишковий член:

Для великих значень t для покращення точності можна використовувати многочлен Ньютона для інтерполяції назад:

Аналогічно отримаємо вираз для другого інтерполяційного многочлена Ньютона.

7). Форми запису інтерполяційного многочлена Ньютона через розділені різниці

Використовуючи вирази для розділених різниць, ми можемо записати явний вираз для інтерполяційного многочлена Ньютона, побудованого на вузлах

У випадку рівновіддалених вузлів можна записати інший вигляд для інтерполяційного многочлена Ньютона. Виразивши розділені різниці через відповідні скінченні різниці отримаємо формулу

Ввівши заміну змінних:

кінцево отримаємо

Ця формула називається інтерполяційним многочленом Ньютона для інтерполяції вперед.

8). Форми запису інтерполяційного многочлена Ньютона через скінченні різниці

Введемо поняття скінчених різниць

перші скінчені різниці вперед.

Можна побудувати скінчені різниці вищих порядків:

Ми можемо виразити скінчені різниці через значення функції в інтерполяційних вузлах:

Можна провести зворотнє перетворення:

Ми побудували скінчені різниці вперед. Аналогічно можна ввести скінчені різниці назад.

Між цими скінченими різницями є простий зв’язок.

9). Точність інтерполяції.

Для великих значень t для покращення точності можна використовувати многочлен Ньютона для інтерполяції назад:

Аналогічно отримаємо вираз для другого інтерполяційного многочлена Ньютона.

10). Алгебраїчні многочлени найкращого квадратичного наближення функцій.

Нехай задано n+1 значення табличної функції в вузлах x₀, x₁, …, x_n. Побудуємо апроксимуючий многочлен методом найменших квадратів. Розглянемо многочлен степені m:

(1)

Коефіцієнти многочлена знайдемо з умови мінімума цільової функції:

(2)

Отримуємо систему рівнянь:

(3)

Для практичного використання систему рівнянь (3) зручно записати у вигляді:

(4)

де введено позначення:

(5)

11). Метод найменших квадратів побудови алгебраїчних многочленів найкращого квадратичного наближення.

Нехай нам задана деяка сітка в вузлах якої відомі значення деякої функції . Розглянемо методику побудови квадратичного наближення алгебраїчним многочленом за методом найменших квадратів. Шукатимемо апроксимуючий многочлен у вигляді

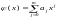Степінь многочлена вибираємо меншим від загального числа вузлів сітки . Коефіцієнти _i знаходимо з умови мінімуму суми квадратів відхилень апроксимуючого многочлена у вузлах: Якщо відома точність отримання значень функції у вузлах , то використовуючи поняття ваги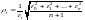 можна отримати уточнену формулу: В цьому випадку апроксимуюча функція буде ближче проходити до вузлів, в яких значення функції отримано точніше. Для знаходження коефіцієнтів ,_, обчислимо частинні похідні і прирівняємо їх до нуля: ... ... Отримаємо систему лінійних алгебраїчних рівнянь рівнянь:

Запишемо систему в компактнішій формі

… Ми ввели скорочені позначення