
Алгоритм Евклида
Этот алгоритм назван в честь Евклида, потому что самое раннее известное его появление – в книге VII Начал. Однако, по мнению многих историков, алгоритм и некоторые его следствия, вероятно, были известны ранее. По меньшей мере, Евклид заслуживает чести за мастерское представление основ теории чисел на базе этого алгоритма.
Евклидов алгоритм используется для нахождения наибольшего общего делителя (НОД) двух положительных целых чисел а и b. Первый
этап
– построить пару
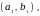 где
где
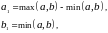
пара,
построенная на
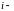 том
шаге ,
том
шаге ,
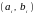
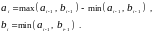
Алгоритм
завершается на первом шаге, когда
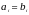 ,
и это общее значение – НОД
,
и это общее значение – НОД
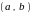 .
Это потому, что вычитание разностей
сохраняет любые общие делители,
следовательно,
.
Это потому, что вычитание разностей
сохраняет любые общие делители,
следовательно,
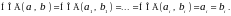
Абсолютная простота алгоритма облегчает выведение некоторых важных следствий. Евклид, конечно, не пользовался нашими обозначениями, но, тем не менее, он получил результаты, близкие к следующим.
Если
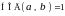 ,
тогда есть целые числа
,
тогда есть целые числа
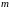 и
и
 ,
такие что
,
такие что
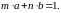
Если р – простое число, которое делит
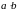 ,
тогда р
делит а
или b
(свойство простого делителя).
,
тогда р
делит а
или b
(свойство простого делителя).
Чтобы
увидеть это, предположим, что р
не делит а.
Тогда, поскольку р
не имеет других делителей, кроме 1, мы
имеем
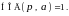 Следовательно,
по предыдущему результату мы получаем
целые числа
и
,
такие
что
Следовательно,
по предыдущему результату мы получаем
целые числа
и
,
такие
что
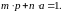 Умножение
каждой стороны на
Умножение
каждой стороны на
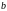 дает
дает
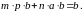
По предположению, р делит , следовательно, р делит оба слагаемых в левой части, и поэтому р делит в правой части.
Каждое положительное целое число имеет однозначное разложение в произведение простых чисел (основная теорема арифметики).
Уравнение Пелля
Диофантово
уравнение
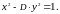 ,
где D
– неквадратное целое число, известно
как уравнение Пелля, потому что Эйлер
ошибочно приписал его решение английскому
математику семнадцатого века Пеллю
(его следовало приписать Браункеру).
Уравнения Пелля, вероятно, самое известное
диофантово уравнение после уравнения
Пифагора. Решение уравнения Пелля –
главный шаг в решении общего квадратного
диофантова уравнения в двух переменных,
а также ключевой инструмент в доказательстве
теоремы Матьясевича, о том, что алгоритма
для решения всех диофантовых уравнений
нет.
,
где D
– неквадратное целое число, известно
как уравнение Пелля, потому что Эйлер
ошибочно приписал его решение английскому
математику семнадцатого века Пеллю
(его следовало приписать Браункеру).
Уравнения Пелля, вероятно, самое известное
диофантово уравнение после уравнения
Пифагора. Решение уравнения Пелля –
главный шаг в решении общего квадратного
диофантова уравнения в двух переменных,
а также ключевой инструмент в доказательстве
теоремы Матьясевича, о том, что алгоритма
для решения всех диофантовых уравнений
нет.
Простой случай уравнения Пелля
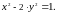
изучался
пифагорейцами в связи с
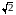 .
Если х,
у
– большие решения этого уравнения,
тогда
.
Если х,
у
– большие решения этого уравнения,
тогда
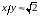 ,
и, фактически, пифагорейцы нашли способ
порождения все больших и больших решений
посредством рекуррентных соотношений
,
и, фактически, пифагорейцы нашли способ
порождения все больших и больших решений
посредством рекуррентных соотношений
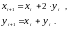
Краткий расчет показывает, что
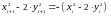
Поэтому,
начиная с тривиального решения
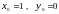 ,
мы получаем последовательно большие
решения
,
мы получаем последовательно большие
решения
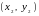 ,
,
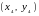 …
Пары
…
Пары
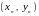 известны
как боковые и диагональные числа, потому
что отношение
известны
как боковые и диагональные числа, потому
что отношение
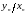
стремится к отношению стороны и диагонали в квадрате.
Но
как, прежде всего, могли быть открыты
эти рекуррентные соотношения? Ван дер
Варден (1976) и Фаулер (1980,1982) предполагают,
что ключ – это евклидов алгоритм,
примененный к отрезкам прямой. При
заданных любых двух длинах а
и
b,
можно определить последовательность
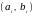 ,
многократным вычитанием меньшей длины
из большей. Если a,
b
– целые кратные некоторой единицы,
тогда процесс завершается, но если b/а
– иррациональное число, он продолжается
бесконечно. Мы вполне можем представить,
что пифагорейцы, как правило, интересовались
,
многократным вычитанием меньшей длины
из большей. Если a,
b
– целые кратные некоторой единицы,
тогда процесс завершается, но если b/а
– иррациональное число, он продолжается
бесконечно. Мы вполне можем представить,
что пифагорейцы, как правило, интересовались
 .
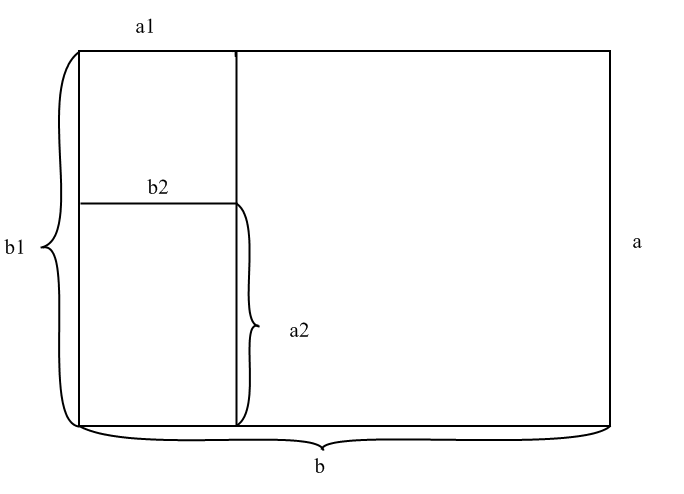
Вот что происходит. Мы представляем a,
b
сторонами прямоугольника, и каждое
вычитание меньшего числа из большего
представлено отсечением квадрата на
более короткой стороне. Мы замечаем,
что прямоугольник, остающийся после
шага 2, со сторонами
.
Вот что происходит. Мы представляем a,
b
сторонами прямоугольника, и каждое
вычитание меньшего числа из большего
представлено отсечением квадрата на
более короткой стороне. Мы замечаем,
что прямоугольник, остающийся после
шага 2, со сторонами
 ,
имеет ту же форму, что и исходный, хотя
длинная сторона теперь вертикальна, а
не горизонтальна. Отсюда следует, что
аналогичные шаги будут повторяться
бесконечно, что, между прочим, является
еще одним доказательством того, что
– иррационально.
,
имеет ту же форму, что и исходный, хотя
длинная сторона теперь вертикальна, а
не горизонтальна. Отсюда следует, что
аналогичные шаги будут повторяться
бесконечно, что, между прочим, является
еще одним доказательством того, что
– иррационально.
В
настоящий момент нас, однако, интересует
соотношение между последовательными
подобными прямоугольниками. Если мы
допустим, что длинная и короткая стороны
последовательных подобных прямоугольников
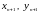 и
и
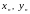 ,
то из рисунка мы можем сделать вывод,
что рекуррентные соотношения для
:
,
то из рисунка мы можем сделать вывод,
что рекуррентные соотношения для
:
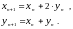
в
точности соотношения пифагорейцев!
Разница заключается в том, что наши
не
являются целыми, и они удовлетворяют
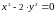 ,
а не
Тем не менее, чувствуешь, что рисунок
дает самую естественную интерпретацию
этих соотношений. Открытие, что те же
самые соотношения порождают решения
,
а не
Тем не менее, чувствуешь, что рисунок
дает самую естественную интерпретацию
этих соотношений. Открытие, что те же
самые соотношения порождают решения
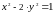 ,
возможно, возникло из желания, чтобы
евклидов алгоритм завершался
,
возможно, возникло из желания, чтобы
евклидов алгоритм завершался
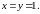 Если пифагорейцы начинали
Если пифагорейцы начинали
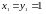 и
применяли рекуррентные соотношения,
то они могли найти, что
и
применяли рекуррентные соотношения,
то они могли найти, что
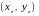 удовлетворяет
удовлетворяет
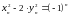 .
.
