Лекция 2

Греческая математика(продолжение)

1. Греческая теория чисел

   1. Числа

   2. Алгоритм Евклида

   3. Уравнение Пелля

2. Бесконечность в греческой математике

   1. Апории Зенона

   2. Метод Исчерпывания

1. Греческая теория чисел

Теория чисел была важной в математике, по меньшей мере, столь же долго, сколь и геометрия, и с основополагающей точки зрения, может быть еще важнее. Несмотря на это, теория чисел никогда не подвергалась систематической трактовке, подобной той, которой подверглась элементарная геометрия в Началах Евклида. На всех этапах своего развития теория чисел имела бросающиеся в глаза пробелы, вследствие трудноразрешимости элементарных задач. Большая часть действительно нерешенных старых задач в математике, в сущности, – простые вопросы о натуральных числах 1, 2, 3,... Отсутствие общего метода решения диофантовых уравнений и задача установления простых чисел вида 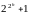уже отмечались. Как следствие, роль теории чисел в истории математики совершенно отличалась от роли геометрии. Геометрия играла стабилизирующую и объединяющую роль, вплоть до задержки иногда дальнейшего развития и создания популярного впечатления, что математика – статичный предмет. Для тех, кто способен понять ее, теория чисел оставалась стимулом к прогрессу и переменам. Лишь меньшинство математиков внесли вклад в успехи теории чисел, но в их число входят несколько великих: Диофант, Ферма, Эйлер, Лагранж и Гаусс. Тем не менее, в теории чисел есть темы, которые слишком интересны, чтобы их проигнорировать, даже если они представляются (в настоящее время) лежащими за пределами основного потока.

1. Числа

Пифагорейцы стремились найти в природе и обществе неизменное. В поисках вечных законов вселенной они изучали геометрию, арифметику, астрономию и музыку. Самым выдающимся их представителем был Архит из Тарента, который жил около 400 г. до н. э. и школе которого, если мы примем гипотезу Франка (Е. Frank), следует приписать большую часть пифагорейской математики. Арифметика пифагорейцев была в высшей степени спекулятивной наукой и имела мало общего с современной ей вычислительной техникой Вавилона. Числа разбивались на классы: четные, нечетные, четно-четные, нечетно-нечетные, простые и составные, совершенные, дружеские, треугольные, квадратные, пятиугольные и т. д.

Многоугольные числа, которые изучали пифагорейцы, вытекают из наивного переноса геометрических идей в теорию чисел. Не считая труда Диофанта, который включает впечатляющие результаты по суммам квадратов, результаты греков по многоугольным числам были элементарного рода. В целом, греки, по-видимому, ошибались, придавая столь важное значение многоугольным числам. О них нет значительных теорем, за исключением, пожалуй, следующих двух. Первая – теорема, о которой сделал предположение Баше де Мезериак (1621) (в своем издании трудов Диофанта), что каждое положительное целое число есть сумма четырех целых квадратов. Это доказал Лагранж (1770). Обобщение, которое Ферма (1670) сформулировал без доказательства, – что каждое положительное целое число есть сумма n n-угольных чисел. Это доказано Коши (1813), хотя доказательство немного недостаточно, потому что все числа, кроме четырех, могут быть 0 или 1. Другая замечательная теорема о многоугольных числах – формула

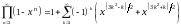
доказанная Эйлером (1750) и известна как теорема Эйлера о пятиугольных числах, поскольку экспоненты 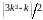– пятиугольные числа.

Простые числа также рассматривались в геометрических рамках, как числа, не имеющие прямоугольного представления. Простое число, не имеющее делителей кроме себя самого и 1, имеет только «линейное» представление. Конечно, это ничто иное, как новая формулировка определения простого числа, а большинство теорем о простых числах требуют гораздо более мощных идей; однако греки действительно вырастили одну жемчужину. Это доказательство, что имеется бесконечное множество простых чисел, в Книге IX Начал Евклида.

При заданной любой конечной совокупности простых чисел 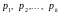, мы можем найти еще одну, рассмотрев

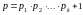
Это число неделимо на (каждое дает остаток 1). Отсюда, либо само р – простое число, и 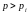, либо оно имеет простой делитель

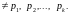
Совершенное число – это число, которое равняется сумме своих делителей (включая 1, но исключая самого себя). Например, 6=1 + 2 + 3 –совершенное число, как и 28 = 1 + 2 + 4 + 7+14. Хотя это понятие восходит к пифагорейцам, известны лишь две заслуживающие внимание теоремы о совершенных числах. Евклид завершает Книгу IX Начал, доказав, что если 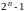– простое число, то 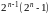– совершенное. Эти совершенные числа, конечно, четные, и Эйлер (1849) (посмертная публикация) доказал, что каждое четное совершенное число имеет евклидов вид. Неизвестно, есть ли какие-либо нечетные совершенные числа; может быть, это старейшая открытая задача в математике.

В силу теоремы Эйлера, существование четных совершенных чисел зависит от существования простых чисел вида . Они известны как простые числа Мерсенна, в честь Марена Мерсенна (1588-1648), который первым привлек внимание к проблеме принятия простых чисел этого вида. Неизвестно, существует ли бесконечное множество чисел Мерсенна, хотя, по-видимому, все большие числа находят довольно постоянно. В последние годы любое новое всемирно зафиксированное простое число было простым числом Мерсенна, давая соответствующее всемирно зафиксированное совершенное число.