
- •І. Характеристика дисципліни
- •У результаті вивчення дисципліни студент повинен
- •Теоретичної механіки
- •1.1. Сила. Система сил. Рівновага абсолютно твердого тіла
- •1.2. Аксіоми статики та їх наслідки
- •Питання для самоконтролю
- •2.1 Проекція сили на вісь і на площину. Аналітичний спосіб задавання сили
- •2.2 Зведення збіжних сил до рівнодійної
- •2.3. Умови рівноваги системи збіжних сил
- •3.3. Момент сили відносно осі
- •3.4. Залежність між моментами сили відносно точки і відносно осі, яка проходить через цю точку
- •3.5 Теорія пар сил
- •4.2. Головний вектор і головний момент довільної системи сил. Основна теорема статики твердого тіла
- •4.3. * Статичні інваріанти
- •4.7 Зведення системи сил до двох сил
- •4.8. Умови рівноваги довільної просторової системи сил
- •4.10. Поняття про статично визначені і статично невизначені задачі. Рівновага системи тіл
2.3. Умови рівноваги системи збіжних сил
Доведемо теорему: "Для рівноваги системи збіжних сил необхідно і достатньо, щобрівнодійна сила дорівнювала нулеві", тобто
![]() (2.9)
(2.9)
Необхідність
умови
(2.9) випливає з того, що система збіжних
сил, прикладених до твердого тіла,
еквівалентна одній силі - рівнодійній
![]() .
Вочевидь, що під дією однієї сили тіло
буде перебувати в рівновазі тільки
тоді, коли ця сила дорівнює нулеві.
.
Вочевидь, що під дією однієї сили тіло
буде перебувати в рівновазі тільки
тоді, коли ця сила дорівнює нулеві.
Для доведення достатності покажемо, що коли рівнодійна сила дорівнює нулю, то система збіжних сил знаходиться у рівновазі. Задана система сил еквівалентна рівнодійній, яка дорівнює нулю.
Отже, дана система сил є врівноваженою (еквівалентною нулю) і вона залишає те тіло, на яке вона діє, в рівновазі.
Теорема доведена.
Враховуючи
умову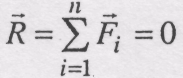 ,
приходимо до висновку, що многокутник
сил
,
приходимо до висновку, що многокутник
сил
![]() є
замкнутим. Останнє
виражає в
графічній формі умову рівноваги системи
збіжних сил.
є
замкнутим. Останнє
виражає в
графічній формі умову рівноваги системи
збіжних сил.
На основі виразу (2.9), враховуючи (2.6) і (2.7), одержуємо:
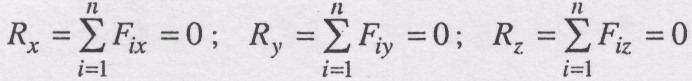 . (2.10)
. (2.10)
Ці умови називаються аналітичними умовами рівноваги збіжних сил і формулюються наступним чином: для рівноваги просторової збіжної системи сил необхідно і достатньо, щоб алгебраїчні суми проекцій сил на три взаємно перпендикулярні осі дорівнювали нулю.
У випадку рівноваги системи збіжних сил, розміщених в одній площині, наприклад Оxy, маємо
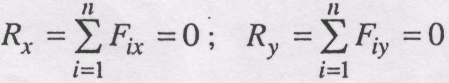 (2.11)
(2.11)
Отже, для рівноваги системи збіжних сил, які лежать в площині, необхідно і достатньо, щоб алгебраїчні суми проекцій цих сил на дві взаємно перпендикулярні осі дорівнювали нулю.
Питання для самоконтролю
Яка система сил називається збіжною?
Що називається силовим многокутником?
В чому полягає графічний метод визначення рівнодійної сили?
Яка графічна умова рівноваги збіжної системи сил?
Які рівняння рівноваги просторової і плоскої системи збіжних сил?
Задача 2.1.
Однорідний циліндр, вага якого Р, розміщений між двома гладкими похилими площинами, які складають з горизонтом кути α і β (рис. 2.5).
Знайти тиск циліндра на обидві площини.
Розв 'язання
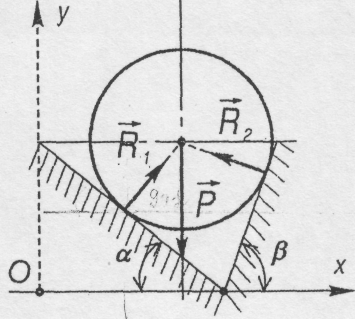 1.Розглянемо
рівновагу циліндра.
1.Розглянемо
рівновагу циліндра.
2.Покажемо активну силу Р -- вагу циліндра.
3.Звільнимо
циліндр від в'язей. В'язями в даному
випадку є дві похилі площини і реакції
![]() і
і
![]() .
направлені перпендикулярно до площин,
тобто до осі циліндра (рис. 2.5).
.
направлені перпендикулярно до площин,
тобто до осі циліндра (рис. 2.5).
4.Вибираємо систему координат, як показано на рис. 2.5.
5.На циліндр діє плоска система збіжних сил. Складемо для неї рівняння рівноваги:
Рис. 2.5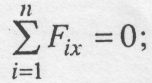
![]()
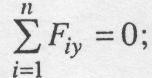
![]()
6.Розв'язуючи одержані рівняння, знаходимо

Шукані
тиски будуть рівні (згідно аксіоми 4) за
величиною і протилежні за напрямом
реакцій
![]() і
і
![]() .
.
Задача 2.2.
Балка А В підтримується в горизонтальному положенні стержнем CD. Закріплення в точках А, С, D - шарнірні.
Визначити реакції шарніра А і стрижня CD. якщо на кінці балки діє вертикальна сила F = 5 кН. Розміри вказані на рис. 2.6. Вагою балки нехтуємо.
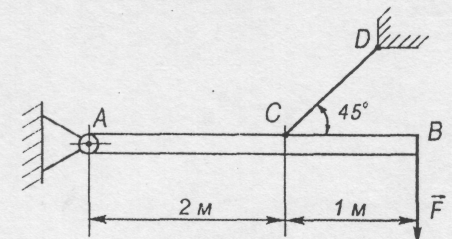 Розв'язання:
Розв'язання:
1.Розглядаємо рівновагу балки А В.
2.Показуємо
активну силу
![]()
Рис. 2.6![]() .
реакції шарніра А
і
стержня DC
перетинаються
в одній точці (теорема про три сили)
(рис. 2.7).
.
реакції шарніра А
і
стержня DC
перетинаються
в одній точці (теорема про три сили)
(рис. 2.7).
4.Вибираємо осі координат як вказано на рис.2.7.
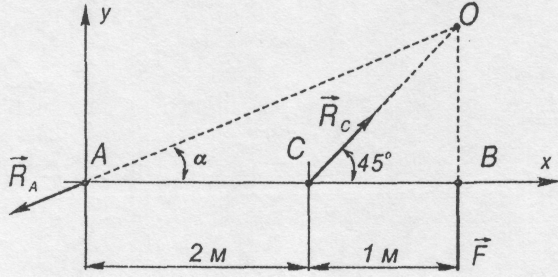
Рис. 2.7
На балку діє плоска система збіжних сил. Складемо рівняння рівноваги:
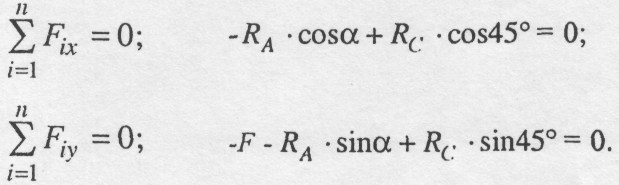
Звідси:

Оскільки
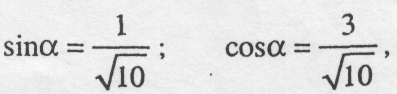
то RA = 7,9 кН, а Rc =10,6 кН.
Задача 2.3.
Знайти зусилля в тросі AD і в стрижнях АВ та АС, які підтримують вантаж Q , вагою 300 Н.
Дано:![]() ;
;![]() ;
;![]() ;
ВК
= СК (рис.
2.8).
;
ВК
= СК (рис.
2.8).
Розв'язання
1.Розглянемо
рівновагу вузла А.
Згідно
принципу звільнення твердих тіл від
в'язей. дію стрижнів і троса на вузол
А
замінюємо
реакціями
![]() .
Таким чином, одержуємо просторову
систему збіжних сил (рис. 2.9).
.
Таким чином, одержуємо просторову
систему збіжних сил (рис. 2.9).
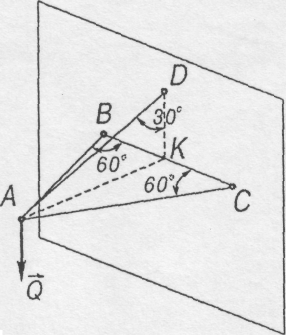
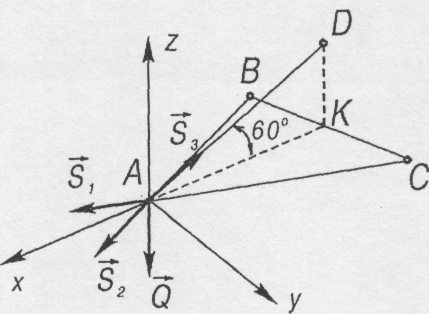
Рис. 2.8 Рис. 2.9
2.Складаємо рівняння рівноваги:
![]()
![]()
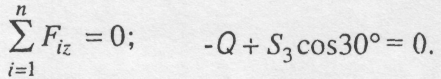
Звідки
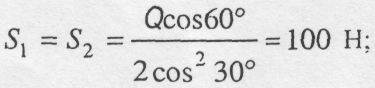
![]()
РОЗДІЛ 3. МОМЕНТИ СИЛИ ВІДНОСНО ТОЧКИ І ОСІ. ПАРА СИЛ.
3.1. Момент сили відносно точки
Моментом
сили
![]() відносно
точки О (центра) називається вектор, що
дорівнює векторному добутку радіуса-вектора
відносно
точки О (центра) називається вектор, що
дорівнює векторному добутку радіуса-вектора
![]() ,
проведеного з центра О в точку А
прикладення сили на вектор сили
,
проведеного з центра О в точку А
прикладення сили на вектор сили
![]() (рис.
3.1).
(рис.
3.1).
![]()
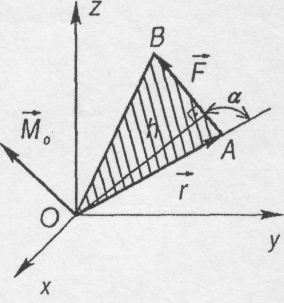 (3.1)
(3.1)
Модуль моменту сили
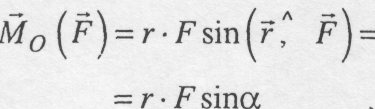 (3.2)
(3.2)
Рис. 3.1![]() .
Довжину цього перпендикуляра h
назвемо
плечем
сили
.
Довжину цього перпендикуляра h
назвемо
плечем
сили
![]() відносно
центра О.
Тоді
вираз (3.2) записується у вигляді:
відносно
центра О.
Тоді
вираз (3.2) записується у вигляді:
![]() (3.3)
(3.3)
Таким
чином, момент
сили![]() відносно центра О чисельно дорівнює
добутку сили на плече і направлений
перпендикулярно площині, що проходить
через точку О і лінію дії сили, в той
бік, звідки "обертання" тіла під
дією сили відносно точки О (або найкоротший
поворот вектора
відносно центра О чисельно дорівнює
добутку сили на плече і направлений
перпендикулярно площині, що проходить
через точку О і лінію дії сили, в той
бік, звідки "обертання" тіла під
дією сили відносно точки О (або найкоротший
поворот вектора![]() до суміщення з вектором
до суміщення з вектором
![]() )
було б видно проти руху стрілки годинника
(рис.
3.2).
)
було б видно проти руху стрілки годинника
(рис.
3.2).
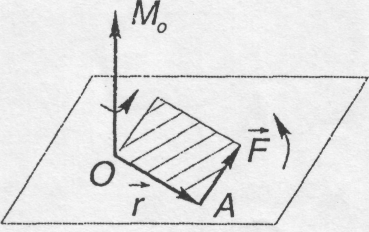
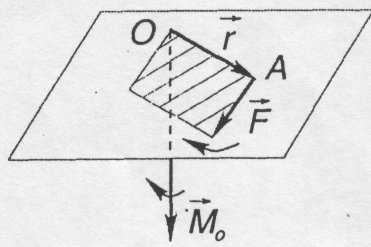
Рис. 3.2
З
рівняння (3.1) можна знайти проекції
вектора
![]() на
осі
декартової прямокутної системи координат,
початок якої збігається з центром
момента О.
3
векторної алгебри відомо, що векторний
добуток
на
осі
декартової прямокутної системи координат,
початок якої збігається з центром
момента О.
3
векторної алгебри відомо, що векторний
добуток
![]() можна представити визначником
можна представити визначником
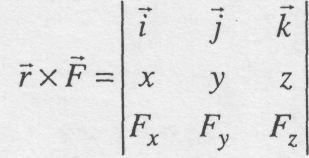 (3.4)
(3.4)
де
![]() - орти вибраної системи координат;
- орти вибраної системи координат;
х,
у,
z
-
проекції вектора
![]() на координатні осі;
на координатні осі;
Fx
,
Fy
, Fz
-
проекції вектора сили![]() на осі координат.
на осі координат.
Розкриваючи
цей визначник за елементами першого
рядка і, розкладаючи вектор
![]() на складові
на складові![]() ,
,
![]() ,
,
![]() ,
одержимо
,
одержимо
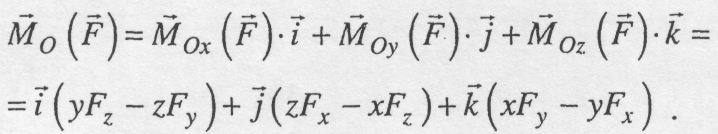 (3.5)
(3.5)
Зрівнюючи
ліву та праву частини цієї рівності,
знаходимо проекції моменту
![]() на осі координат:
на осі координат:
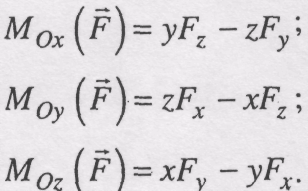 (3.6)
(3.6)
Проекції
![]() ,
,
![]() ,
,
![]() моменту сили
моменту сили
![]() на
осі координат називаються також моментами
сили відносно координатних осей.
на
осі координат називаються також моментами
сили відносно координатних осей.
Формули
(3.6) є аналітичними
виразами проекцій на координатні
осі моменту сили![]() відносно центра О.
відносно центра О.
Знаючи вирази (3.6), модуль і напрям моменту сили відносно центра визначаємо наступним чином:
![]()
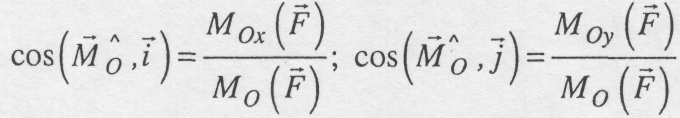 (3.7)
(3.7)
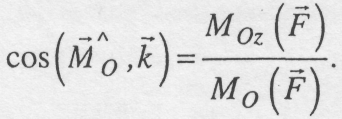
З визначення моменту сили відносно точки випливає:
1. Якщо переміщувати точку прикладання сили вздовж лінії дії сили, то момент сили відносно точки не зміниться.
2. Момент сили відносно точки дорівнює нулю, якщо лінія дії сили проходить через цю точку (h = 0).
3.
Момент сили відносно точки чисельно
дорівнює подвійній площі трикутника
ОАВ
(рис.
3.1), тобто
![]() .
.
4.
Момент сили відносно точки є зв'язаним
вектором, оскільки
![]() не дорівнює
не дорівнює
![]() (площа трикутника ОАВ
не
дорівнює площі трикутника О1АВ)
(рис.
3.3).
(площа трикутника ОАВ
не
дорівнює площі трикутника О1АВ)
(рис.
3.3).

Рис. 3.3
3.2. Теорема про момент рівнодійної системи збіжних сил (теорема Варіньона)
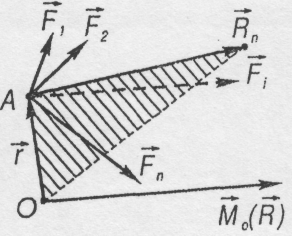 Доведемо
теорему: "Момент
рівнодійної системи збіжних сил відносно
довільного центра дорівнює векторній
(геометричній) сумі моментів складових
сил відносно того ж самого центра".
Доведемо
теорему: "Момент
рівнодійної системи збіжних сил відносно
довільного центра дорівнює векторній
(геометричній) сумі моментів складових
сил відносно того ж самого центра".
 (3.8)
(3.8)
Доведення:
Рис. 3.4![]() ).
).
Позначимо![]() -
радіус-вектор точки А
відносно
довільного центра О.
-
радіус-вектор точки А
відносно
довільного центра О.
Рівнодійна заданої системи сил дорівнює
![]()
Тоді з визначення моменту сили відносно точки О маємо:
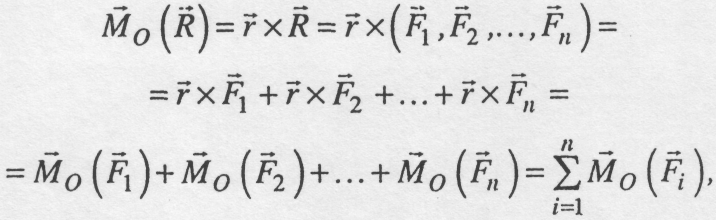 (3.9)
(3.9)
що й потрібно було довести.
Слід зазначити, що ця теорема узагальнюється на випадок будь-якої системи, що зводиться до рівнодійної. Якщо сили і точка О розміщені в одній площині, то їх моменти перпендикулярні до цієї площини і лежать на одній прямій. Тому момент рівнодійної такої системи сил дорівнює алгебраїчній сумі моментів складових сил відносно цієї точки.
![]() (3.10)
(3.10)
