
- •9.1. Завдання руху твердого тіла
- •9.2 Поступальний рух твердого тіла
- •9.3. Обертальний рух твердого тіла навколо нерухомої осі
- •9.4. Швидкості і прискорення точок тіла,що обертається навколо нерухомої осі
- •10.1. Кінематичні рівняння руху
- •10.2 Швидкості точок тіла при плоскопаралельному русі
- •10.3* План швидкостей
- •10.5 Прискорення точок тіла при плоскопаралельному русі
10.1. Кінематичні рівняння руху
Пласко паралельним називається такий рух твердого тіла, при якому кожна його точка рухається в одній і тій площині, паралельній деякій нерухомій площині.
Прикладом тіла, що здійснює плоскопаралельний (плоский ) рух може служити циліндр, що котиться по горизонтальній площині (рис. 10.1). Всі точки циліндра переміщуються у площинах, паралельних площині Oyz . Окремі ланки більшості існуючих механізмів здійснюють плоскопаралельний рух.
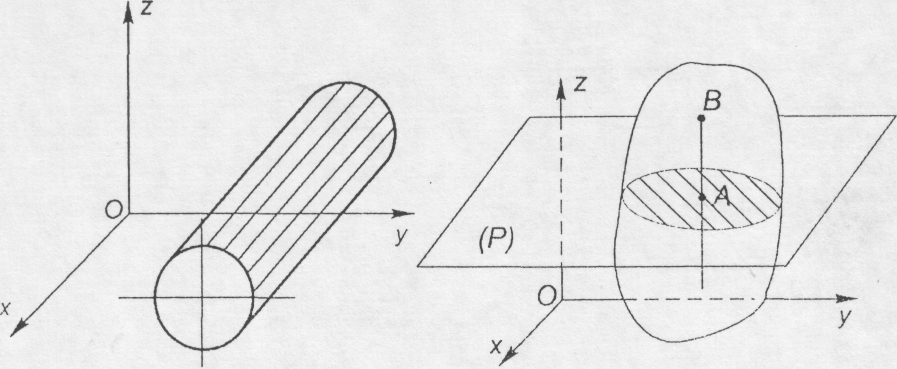
Рис. 10.1 Рис. 10.2
Розглянемо довільний плоскопаралельний рух твердого тіла. Нехай всі точки тіла переміщуються у площинах, паралельних нерухомій площині Оху . Пересічемо тіло площиною Р , паралельною нерухомій площині. З визначення плоского руху і властивостей твердого тіла випливає, що будь-яка пряма АВ , проведена в тілі перпендикулярно площині Оху, буде переміщуватись поступально, тобто траєкторії, швидкості і прискорення всіх точок цієї прямої будуть однаковими. Таким чином, для визначення руху тіла необхідно знати рух лише однієї точки на кожній прямій, проведеній перпендикулярно площині Оху . Вибравши точки в одній площині, паралельній площині Оху , ми можемо стверджувати, що плоский рух тіла повністю визначається рухом плоскої фігури, одержаної від перетину тіла будь-якою площиною, паралельною площині Оху . Тому в подальшому ми будемо зображати тільки плоску фігуру - переріз тіла і вивчати рух точок тіла цього перерізу у своїй площині.
В свою чергу, положення плоскої фігури в своїй площині, повністю визначається положенням двох яких-небудь її точок, наприклад. А і В , отже відрізком АВ .
Розглянемо плоский рух фігури S у своїй площині (рис. 10.2).
Початок рухомої системи координат Аxy , яка рухається поступально відносно нерухомої Ох1у1 , помістимо в довільну точку фігури А , яку в подальшому будемо називати полюсом.
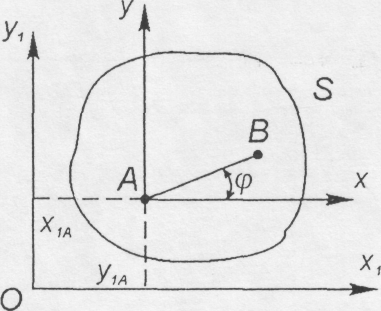
Рис. 10.2
Рух
плоскої фігури буде визначено, якщо
будуть задані: функції часу координати
точки А(х1А,у1А}
і
кут повороту
![]() плоскої фігури навколо точки А :
плоскої фігури навколо точки А :
![]() (10.1)
(10.1)
Ці співвідношення являють собою кінематичні рівняння твердого тіла, що здійснює плоскопаралельний рух.
Таким
чином, плоский рух твердого тіла має
три ступені вільності, оскільки рух
тіла визначається трьома незалежними
параметрами х1Aу1А
і
і![]() .
.
10.2 Швидкості точок тіла при плоскопаралельному русі
Нехай
В
- довільна
точка плоскої фігури. Радіус-вектор
![]() визначаючий її положення відносно
нерухомої системи координат Ox1y1
(рис.
10.3),
можна задати з допомогою двох векторів:
визначаючий її положення відносно
нерухомої системи координат Ox1y1
(рис.
10.3),
можна задати з допомогою двох векторів:
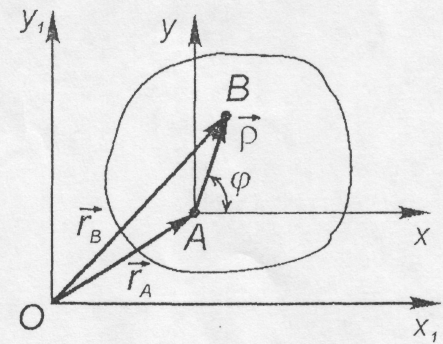
Рис. 10.3
![]()
![]()
Диференціюючи це рівняння за часом, одержимо:
 (10.2)
(10.2)
Зазначимо,
що
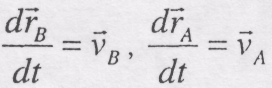 ,
а вектор
,
а вектор
![]() для
спостерігача, що знаходиться в системі
координат Аху,
цей вектор визначає швидкість точки.
Введемо для неї позначення:
для
спостерігача, що знаходиться в системі
координат Аху,
цей вектор визначає швидкість точки.
Введемо для неї позначення:
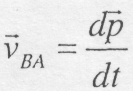 .
.
Однак, рух тіла відносно цієї системи координат являє собою обертання тіла навколо нерухомої осі Az , направленої перпендикулярно площині рисунка (рис. 10.3) до читача, тобто швидкість, є швидкість точки В при обертанні тіла навколо осі Az. Для визначення цієї швидкості була одержана формула (8.13), яка записується у вигляді:
![]()
де![]() - миттєва кутова швидкість обертання
фігури навколо полюса А
(навколо
осі az
).
- миттєва кутова швидкість обертання
фігури навколо полюса А
(навколо
осі az
).
Формула (10.2) прийме тепер вигляд
![]() (10.3)
(10.3)
Покажемо, що кутова швидкість обертання фігури не залежить від вибору полюса.
Нехай А і В - дві будь-які точки плоскої фігури. Для визначення швидкостей цих точок можна скористатись формулами (10.3):
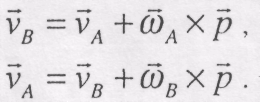
Склавши обидві рівності, одержимо:
![]()
Замітимо,
що вектор
![]() перпендикулярний до площини фігури,
тобто кут між цим вектором і вектором
перпендикулярний до площини фігури,
тобто кут між цим вектором і вектором
![]() дорівнює
90°, тому одержана рівність може
виконуватись в єдиному випадку, коли
дорівнює
90°, тому одержана рівність може
виконуватись в єдиному випадку, коли
![]() .
Таким чином, немає необхідності надалі
зберігати індекс полюса в позначенні
вектора кутової швидкості, тобто
.
Таким чином, немає необхідності надалі
зберігати індекс полюса в позначенні
вектора кутової швидкості, тобто
![]()
Звідси формула (10.3) може бути записана у вигляді
![]() (10.4)
(10.4)
тобто, швидкість будь-якої точки плоскої фігури дорівнює геометричній сумі швидкості полюса і швидкості точки при обертанні плоскої фігури навколо полюса.
Так
як
![]() ,
то величина швидкості обертання точки
В
навколо
полюса дорівнює:
,
то величина швидкості обертання точки
В
навколо
полюса дорівнює:
![]() (10.4а)
(10.4а)
так
як вектор
![]() - миттєва
кутова швидкість обертання фігури
направлений перпендикулярно до площини
рисунка.
- миттєва
кутова швидкість обертання фігури
направлений перпендикулярно до площини
рисунка.
Відмітимо,
що вектор
![]() перпендикулярний також до АВ
. Направлення
обертання плоскої фігури навколо полюса
залежить тільки від знаку проекції
кутової швидкості на вісь Az
.
Так
як
перпендикулярний також до АВ
. Направлення
обертання плоскої фігури навколо полюса
залежить тільки від знаку проекції
кутової швидкості на вісь Az
.
Так
як
![]() ,
то
при
,
то
при
![]() обертання проходить проти часової
стрілки і при
обертання проходить проти часової
стрілки і при
![]() -
за часовою стрілкою.
-
за часовою стрілкою.
На
рис. 10.4 а і б показано як, знаючи швидкість
точки А
, можна
знайти швидкість точки В
при
![]() і
і
![]() .
.
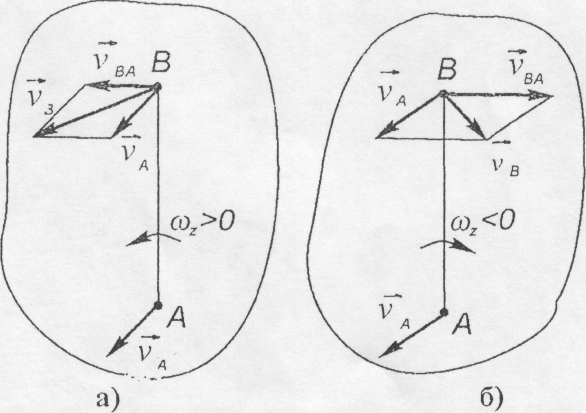
Рис. 10.4
З рівності (10.4) витікає одна корисна теорема
Теорема
При плоскому русі проекції швидкостей двох будь-яких точок плоскої фігури на вісь, що проходить через ці точки, рівні між собою.
Виберемо додатний напрямок для осі АВ , як вказано на рисунку 10.5.
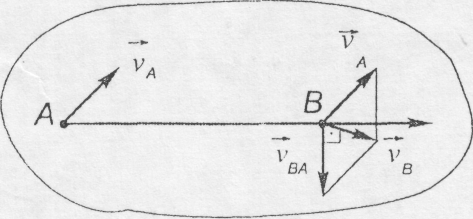
Рис. 10.5
Застосуємо формулу (10.4):
![]()
Проектуючи цю рівність на направлення АВ , одержимо
![]()
Останній
член цієї рівності пропадає, так як
вектор
![]() перпендикулярний
АВ
і,
отже,
перпендикулярний
АВ
і,
отже,
![]()
Теореми і визначення, викладені в цьому розділі, можна використати для графічного знаходження швидкостей точок плоскої фігури з допомогою побудови плану швидкостей.
