
1. Определение производной
Пусть функция
![]() определена в некоторой точке
определена в некоторой точке
![]() ,
и пусть существует конечный предел
отношения
,
и пусть существует конечный предел
отношения
![]() ,
при
,
при
![]() ,
тогда этот предел называется производной
функции
в точке
,
тогда этот предел называется производной
функции
в точке
![]()
![]() (1)
(1)
Если функция
![]() имеет производную в точке
имеет производную в точке
![]() ,
т.е. существует конечный предел
,
т.е. существует конечный предел
![]() ,
(2)
,
(2)
то существует предельное положение секущей l, заданной уравнением
![]() .
(3)
.
(3)
Это означает, что
в точке
![]() существует касательная
существует касательная
![]() к графику функции
,
причём, согласно формуле
к графику функции
,
причём, согласно формуле
![]() ,
где
,
где
![]() – угловой коэффициент прямой
.
так как
– угловой коэффициент прямой
.
так как
![]() ,
где
,
где
![]() – угол, образуемый касательной с
положительны направление оси абсцисс,
то
– угол, образуемый касательной с
положительны направление оси абсцисс,
то
![]() .
(4)
.
(4)
Таким образом, геометрический смысл производной состоит в том, что производная функции в данной точке равна угловому коэффициенту касательной к графику функции в точке
Уравнение
касательной к графику функции
в точке
,
получаемое из уравнения (3) заменой
![]() на
на
![]() ,
имеет вид
,
имеет вид
. (5)
Записать уравнение касательной к графику функции
 ,
параллельной прямой
,
параллельной прямой
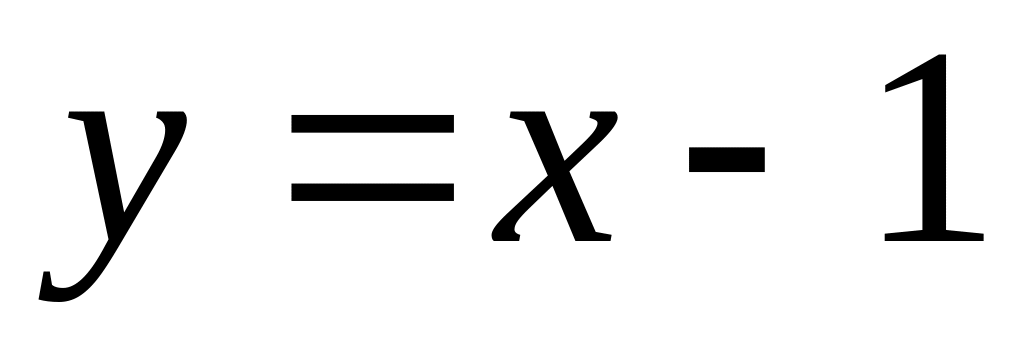 .
.
Так как угловой
коэффициент касательной по условию
равен угловому коэффициенту прямой
,
т.е. равен 1, то из уравнения
![]() получаем
получаем
![]() ,
а по формуле (5) при
,
,
а по формуле (5) при
,
![]() находим уравнение касательной
находим уравнение касательной
![]() .
.
1.2.
Составить уравнение касательной к
функции
![]() в точке
в точке
![]() .
.
Уравнение
касательной к графику функции
в точке
![]() ,
где
,
где
![]() имеет вид:
имеет вид:
![]() .
.
Вычислим производную по формуле (1)

Далее:
![]() .
.
Поэтому уравнение
касательной в точке
![]() имеет вид:
имеет вид:
![]() .
.
Или после упрощения:
![]() .
.
Таблица производных
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()

![]()
![]()
![]()
![]()
2. Дифференциал функции
Если функция
определена в
![]() – окрестности точки
,
а приращение
– окрестности точки
,
а приращение
![]() функции
в точке x0
представимо в виде
функции
в точке x0
представимо в виде
![]() ,
,
где
![]() не зависит от
не зависит от
![]() ,
а
,
а
![]() при
при
![]() ,
то функция
называется дифференцируемой в точке
,
а произведение
,
то функция
называется дифференцируемой в точке
,
а произведение
![]() называется её дифференциалом в точке
x0
и обозначается
называется её дифференциалом в точке
x0
и обозначается
![]() или
.
или
.
2.1. Найти дифференциал
![]()
 .
.
2.2. Вычислить приближенно с помощью дифференциала.
![]()
Для функции
![]() воспользуемся
формулой приближенного вычисления с
помощью дифференциала:
воспользуемся
формулой приближенного вычисления с
помощью дифференциала:
![]() .
Здесь:
.
Здесь:
-
![]() -
значение рассматриваемой функции в
исходной точке.
-
значение рассматриваемой функции в
исходной точке.
-
![]() -
значение рассматриваемой функции в
«хорошей» точке близкой к исходной
точке.
-
значение рассматриваемой функции в
«хорошей» точке близкой к исходной
точке.
-![]() -дифференциал
функции.
-дифференциал
функции.
В нашем случае
![]() .
В качестве «хорошей» точки возьмем
точку
.
В качестве «хорошей» точки возьмем
точку
![]() .
Тогда приращение аргумента есть
.
Тогда приращение аргумента есть
![]() .
.
Вычислим производную
функции
.
Получим:
![]() .
.
Итак, для нашей функции имеем следующую приближенную формулу:
![]() .
.
Тогда, подставляя в нее наши числовые значения получаем:
![]() .
.
Ответ:
![]() .
.
