
Твимс
.docУЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Факультет заочного и дистанционного обучения
Специальность: информационные технологии и управление в технических системах
КОНТРОЛЬНАЯ РАБОТА ПО ДИСЦИПЛИНЕ «ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА»
Вариант №4
Бойчука Вячеслава Анатольевича
Группа №702421
зачётная книжка №702421-04
Электронный адрес: beychik@mail.ru
В задачах 1.1-1.5 подбрасываются две игральные кости.
1.5. Определить вероятность того, что выпадут разные, но четные числа.
№1,5
Решение.
Воспользуемся классическим определением вероятности
Р=![]()
m–число исходов интересующего нас события, выпадут разные числа, но четные числа
m=6 ?????? –перечислить комбинации.
n=62
p=6/36=![]()
Ответ:
р=![]()
№2.15
В задачах 2.1-2.30 приведены схемы соединения элементов, образующих цепь с одним входом и одним выходом. Предполагается, что отказы элементов являются независимыми в совокупности событиями. Отказ любого из элементов приводит к прерыванию сигнала в той ветви цепи, где находится данный элемент. Вероятности отказа элементов 1, 2, 3, 4, 5 соответственно равны p1=0,1; p2=0,2; p3=0,3; p4=0,4; p5=0,5. Найти вероятность того, что сигнал пройдет со входа на выход.
Решение.
Обозначим Аi– событие, состоящее в том, что i-ый элемент выйдет из строя
А– событие состоящее в том, что сигнал пройдет со входа на выход
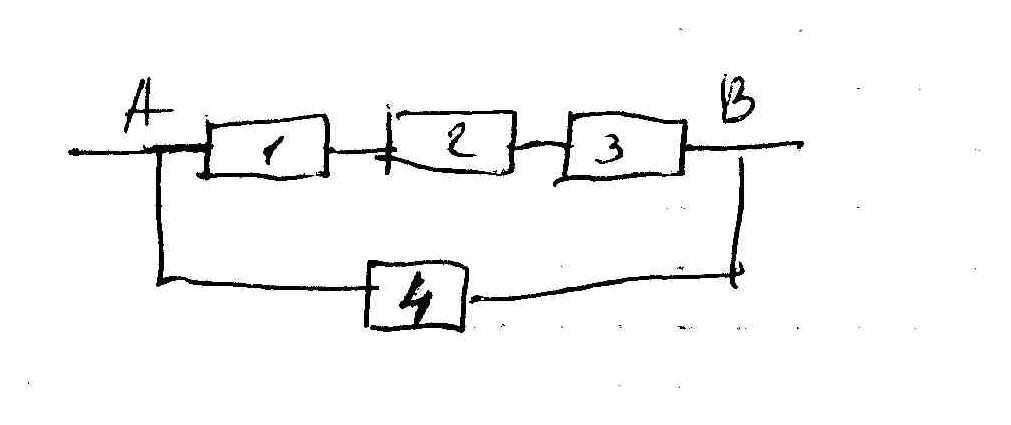
Рассмотрим
событие
![]() –
сигнал не пройдет.
–
сигнал не пройдет.
![]() =
=![]() А4
А4
где
![]() –
событие состоящее в том, что сигнал не
пройдет по участку АВ
–
событие состоящее в том, что сигнал не
пройдет по участку АВ
С=![]()
Вероятность прохождения сигнала через участок АВ так как события Аi независимые, то
Р(С)=
![]()
Р(![]() )=1–
Р(С)=1-
)=1–
Р(С)=1-![]()
Р(![]() )=1–0,9*0,8*0,7=0,496
)=1–0,9*0,8*0,7=0,496
Р(![]() )=Р(
)=Р(![]() )*Р(А4)=0,496*0,4=0,2133
)*Р(А4)=0,496*0,4=0,2133
Вероятность события А
P(A)=1–
Р(![]() )=1–0.2133=0.7867
)=1–0.2133=0.7867
Ответ: Р(А)=0,7867
+
3.15. Прибор состоит из трех блоков. Исправность каждого блока необходима для функционирования устройства. Отказы блоков независимы. Вероятности безотказной работы блоков соответственно равны 0,6; 0,7; 0,8. Определить вероятность того, что откажет два блока.
3.19. Условие задачи 3.15. В результате испытаний прибор вышел из строя. Определить вероятность того, что отказали три блока.
№3.19
Решение.
р1=0,6 р2=0,7 р3=0,8
Обозначим А событие состоящее в том, что прибор отказал
Аi–i-ый блок отказал
Р(А1)=р1 Р(А2)=р2 Р(А3)=р3
Можно выдвинуть четыре гипотезы:
Н1– отказал один блок
Н1=А1![]()
![]() +
А2
+
А2![]()
![]() +
А3
+
А3![]()
![]()
Н2– отказали два блока
Н2=А1А2![]() +
А1
+
А1![]() А3+
А3А2
А3+
А3А2![]()
Н3– отказали три блока
Н3=А1А2А3
Н4– все блоки работают
Н4=![]()
![]()
Р(Н1)=(1–р1)р2р3+(1–р2)р1р3+(1–р3)р2р1=0,4*0,7*0,8+0,6*0,3*0,8+0,6*0,7*0,2=0,452
Р(Н2)=(1–р1)(1–р2)р3+(1–р1)(1–р3)р2+(1–р3)(1–р2)р1=0,4*0,3*0,8+0,4*0,7*0,2+0,6*0,3*0,2=0,188
Р(Н3)=(1–р1)(1–р2)(1–р3)=0,4*0,3*0,2=0,024
Р(Н4)=р1р2р3=0,6*0,7*0,8=0,336
Проверка
Р(Н1)+ Р(Н2)+ Р(Н3)+ Р(Н4)=0,452+0,188+0,024+0,336=1
Условная вероятность отказа прибора, если отказал один блок
РН1(А)=1
Если отказали два блока
РН2(А)=1
Если отказали три блока
РН3(А)=1
Если все блоки работают
РН4(А)=0
Вероятность события А найдем по формуле полной вероятности
Р(А)=Р(Н1)* РН1(А)+ Р(Н2)* РН2(А)+ Р(Н3)* РН3(А)+ Р(Н4)* РН4(А)
Р(А)=0,452*1+0,188*1+0,024*1+0,336*0=0,664
Вероятность того, что прибор вышел из строя по причине поломки трех блоков найдем по формуле Байеса
РА(Н3)=![]()
Ответ: РА(Н3)=0,0361
+
4.1. Вероятность изготовления стандартного изделия равна 0,95. Какова вероятность того, что среди десяти изделий не более одного нестандартного?
№4,1
Решение.
р=0,95 n=10
Вероятность того, что не более одного нестандартного найдем по формуле
Р(к≤1)=Р(к=0)+ Р(к=1)
Вероятность того, что не будет ни одного нестандартного
Р(к=0)=р10=0,9510=0,5987
Р(к=1)=![]() р9(1-р)1=10*0,959*0,05=0,3151
р9(1-р)1=10*0,959*0,05=0,3151
Р(к≤1)=0,5987+0,3151=0,9138
Ответ: Р(к≤1)= 0,9138
+
В задачах 5.1-5.30 дискретная случайная величина Х может принимать одно из пяти фиксированных значений x1, x2, x3, x4, x5 с вероятностями p1, p2, p3, p4, p5 соответственно (конкретные значения приведены в табл. 1.1). Вычислить математическое ожидание и дисперсию величины Х. Рассчитать и построить график функции распределения.
№5,8
|
Х |
-5 |
-2 |
0 |
1 |
2 |
|
Р |
0,1 |
0,2 |
0,1 |
0,3 |
0,3 |
Решение.
Математическое ожидание
М(Х)=![]()
М(Х)=-5*0,1-2*0,2+0*0,1+1*0,3+2*0,3=0
Дисперсия
Д(Х)=М(Х2)–( М(Х))2
Где
М(Х2)=![]()
М(Х2)=(-5)2*0,1+(-2)2*0,2+02*0,1+12*0,3+22*0,3=4,8
Д(Х)=4,8–02=4,8
Функция распределения
F(xi)=P{X<xi}=P{(X=x1)È(X=x2)È ... È(X=xi-1)}= p1+...+pi-1.
F(X)= F(X)=
F(X)=
График функции распределения
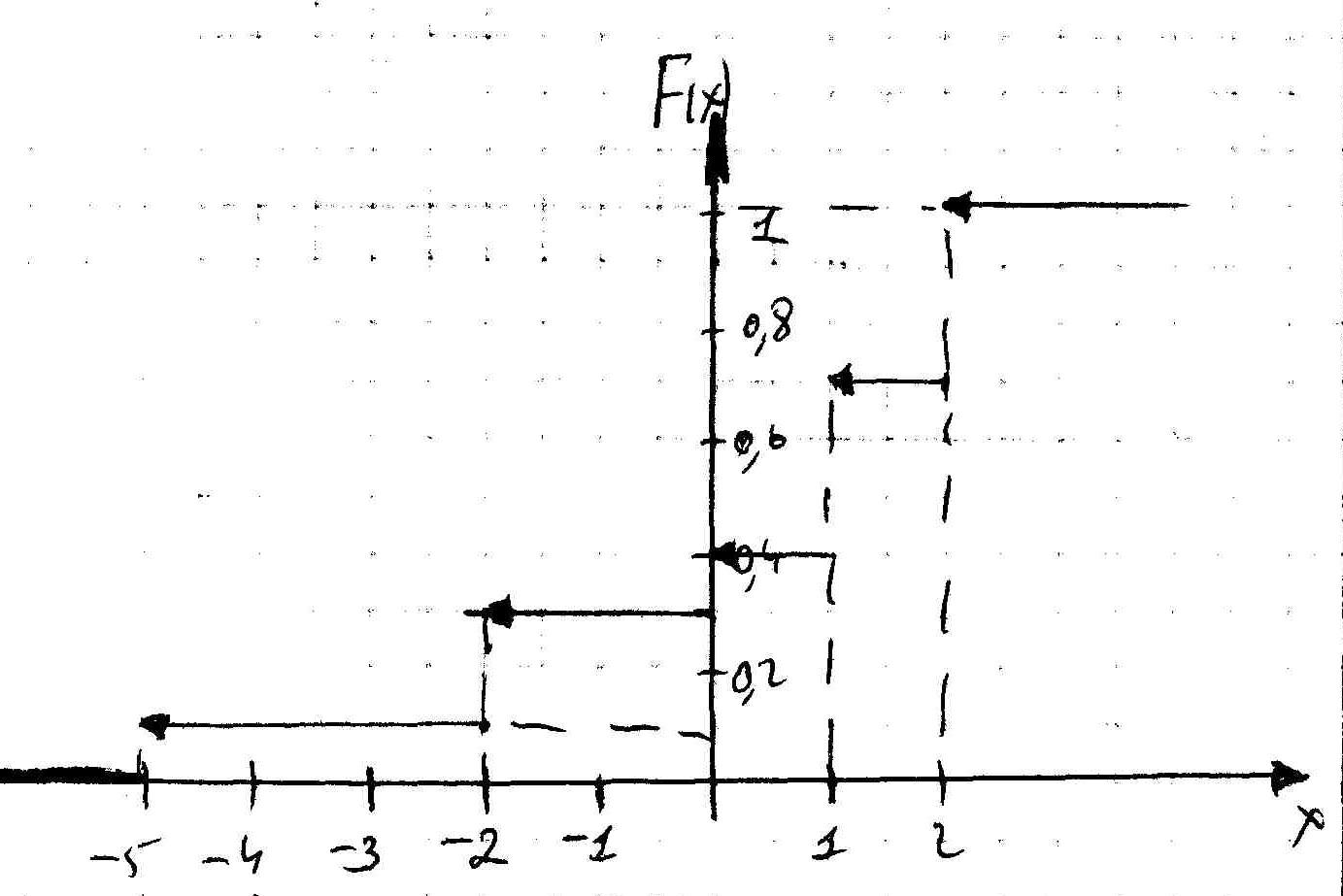
+
В задачах 6.1-6.30 (параметры заданий приведены в табл. 1.2) случайная величина Х задана плотностью вероятности
![]()
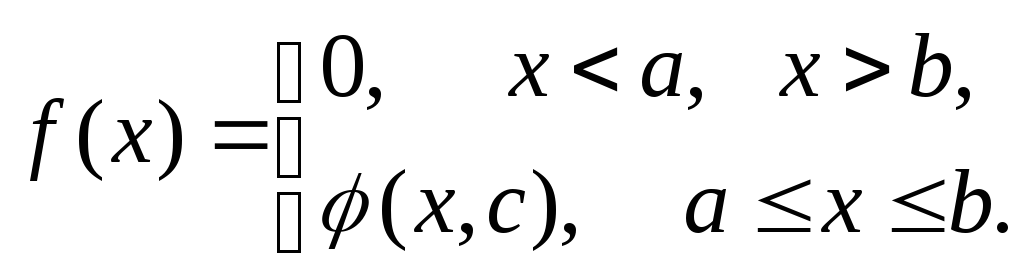
Определить
константу С,
математическое ожидание, дисперсию,
функцию распределения величины Х, а
также вероятность ее попадания в
интервал![]() .
.
№6,14
Решение.
f(x)=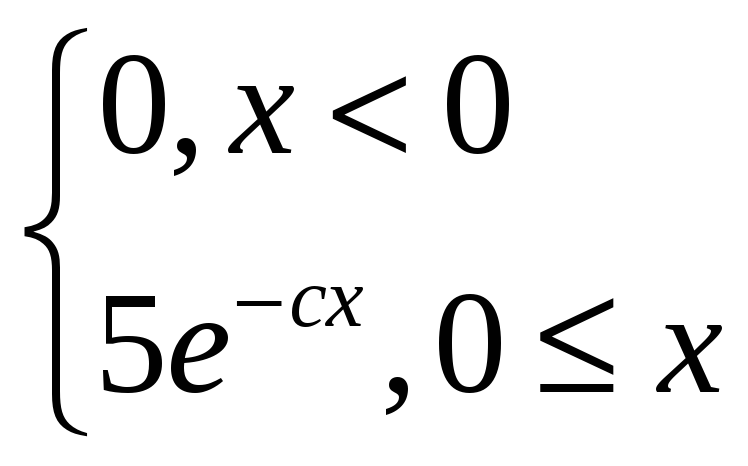
Для определения постоянной с воспользуемся свойством плотности вероятности
![]()
![]()
5/с=1
с=5
f(x)=
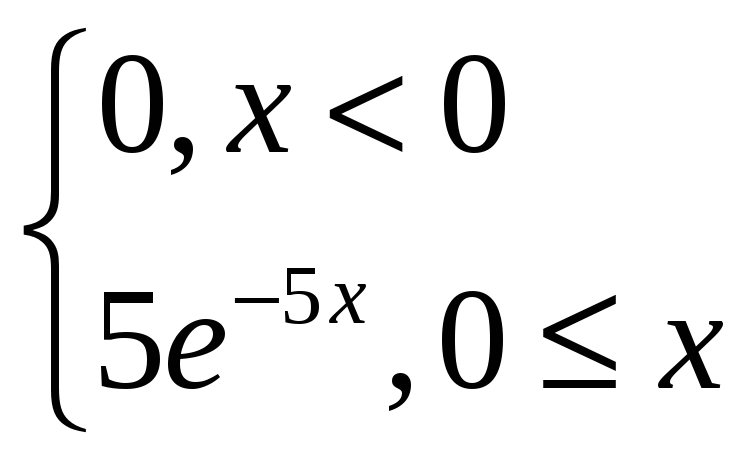
математическое ожидание
М(Х)=![]()
М(Х)=
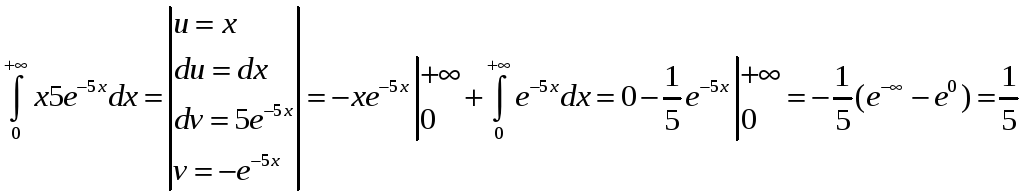
Дисперсия
Д(Х)=М(Х2)–(М(Х))2
Где
М(Х2)=
![]()
М(Х2)=
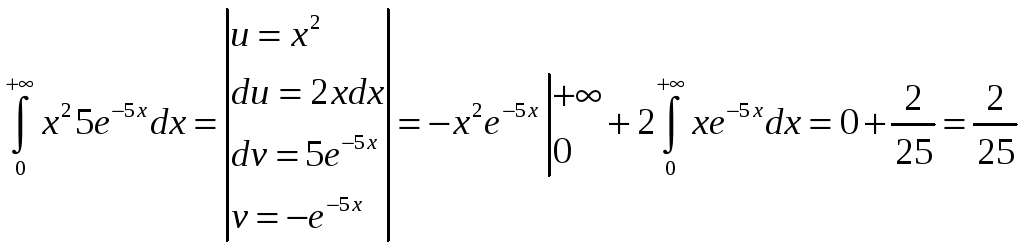
Д(Х)=2/25–(1/4)2=0,0175
Функция распределения
F(x)=![]()
F(X)=![]() при x<0
при x<0
F(X)=![]() при x≥0
при x≥0
F(X)=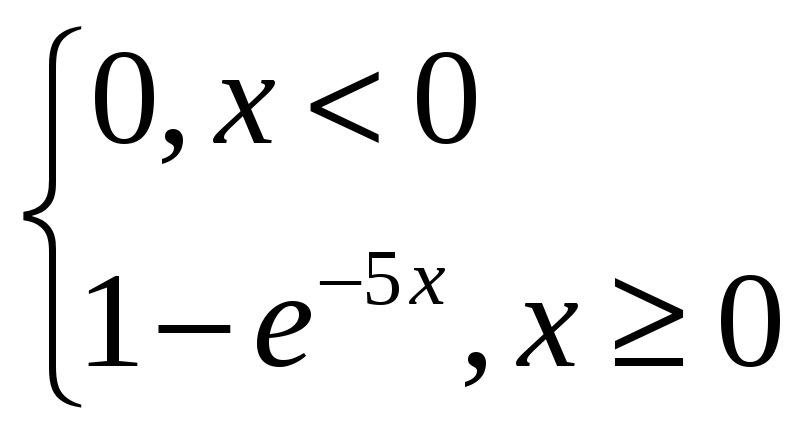
Вероятность того, что 0<x<1 найдем по формуле
Р(0<x<1)=
![]()
В задачах 7.1-7.30 (условия приведены в табл. 1.3) случайная величина Х распределена равномерно на интервале [a,b]. Построить график случайной величины Y=(X) и определить плотность вероятности g(y).
№7.18
Решение.
Y=![]()
Плотность вероятности СВ Х найдем по формуле
f(x)=![]()
f(x)=![]() =4/(π3)
=4/(π3)
График
функции Y=![]() при
–π/4≤x≤
π/2
при
–π/4≤x≤
π/2
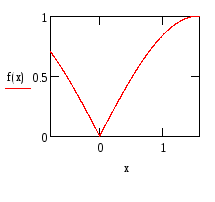
x1=-arcsin(y)
x2= arcsin(y)
x1’=(-arcsin(y))=
-![]()
x2’=(arcsin(y))=
![]()
g(y)=f(ψ(y)) ψ’(y)
Так как функция Y отрезке –π/4≤x≤ π/4 не монотонная, то для нахождения плотности вероятности воспользуемся формулой
g(y)=f(-arcsin(y))*![]() +f(arcsin(y))*
+f(arcsin(y))*
![]() =
=![]() ,
0<y≤
,
0<y≤![]()
На отрезке π/4≤x≤ π/2 функция монотонная
g(y)=
f(arcsin(y))*
![]() =
=![]() ,
,
![]() <y≤1
<y≤1
Ответ:
g(y)=
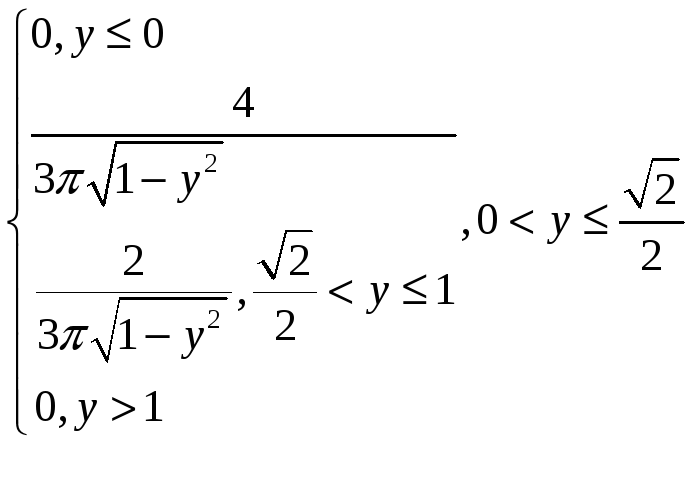 +
+
В задачах 8.1-8.30 (конкретные параметры приведены в табл. 1.4) двухмерный случайный вектор (Х, У) равномерно распределен внутри выделенной жирными прямыми линиями на рис. 1.1 области B. Двухмерная плотность вероятности f(x,y) одинакова для любой точки этой области B:
![]()
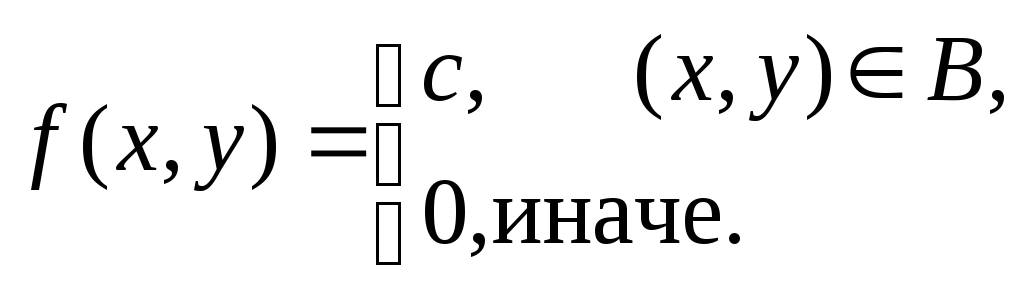
Вычислить коэффициент корреляции между величинами X и Y.
№8.11
Решение.
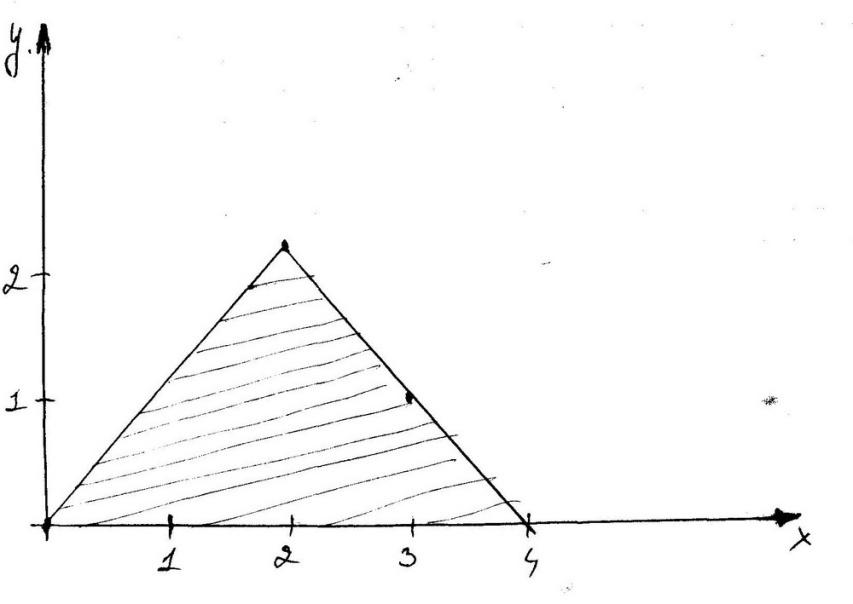
y=x
y=4-x
Коэффициент корреляции
r=![]()
плотность распределения СВ (x,y) найдем по формуле
f(x,y)=1/S
где S–площадь фигуры
S=0.5*2*4=4
f(x,y)=1/4
Плотность распределения f(x) найдем по формуле
f(x)=![]()
f(x)=
![]() ,
0<x≤2
,
0<x≤2
f(x)=
![]() ,
2<x≤4
,
2<x≤4
f(x)=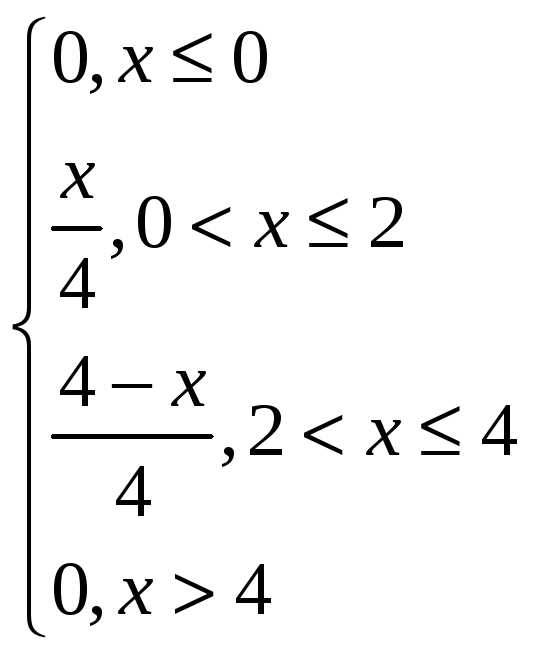
f(y)=
![]()
f(y)=
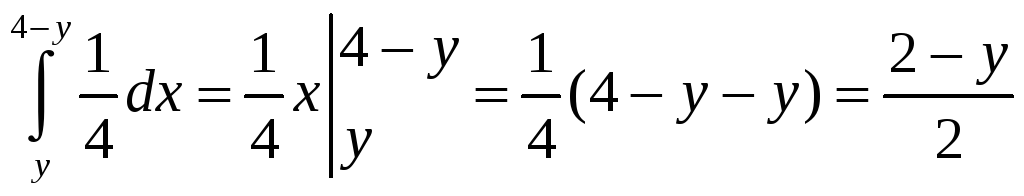 ,0<y≤2
,0<y≤2
f(y)=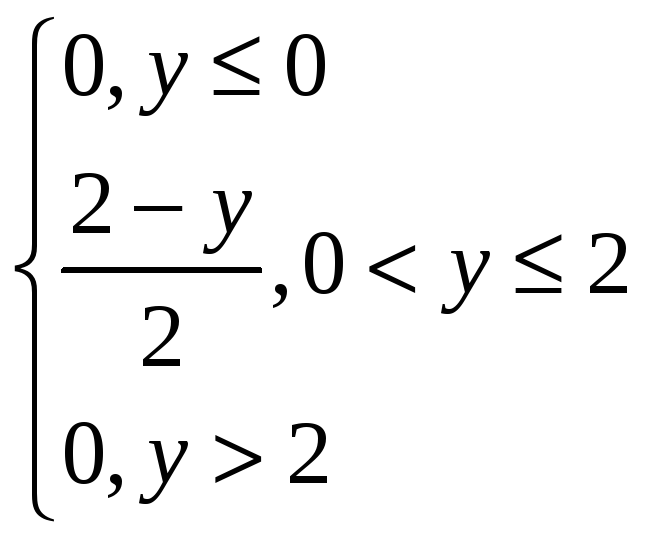
Математическое ожидание
М(Х)=![]()
М(Y)=![]()
![]()
М(Y)=
![]()
К=![]()
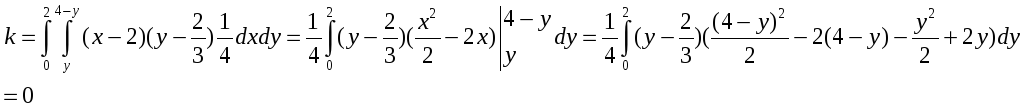
Среднее квадратическое отклонение
![]()
![]()
![]()
![]()
М(Y2)=
![]()
![]()
r=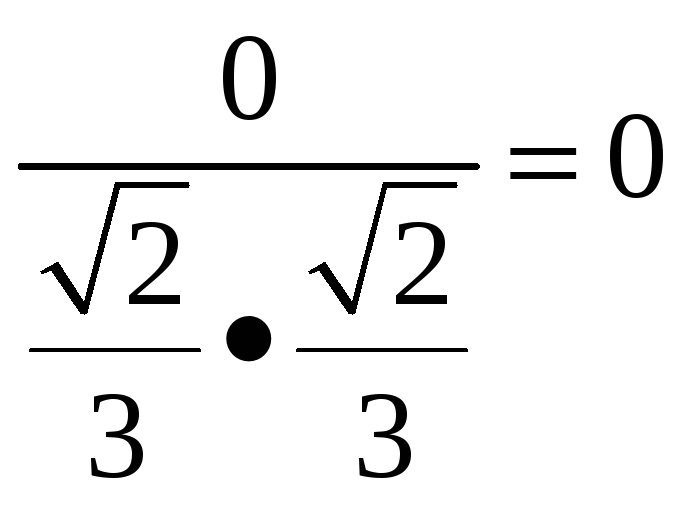
r=0
Ответ: r=0
+
В задачах 9,1-9,40вычислить математическое ожидание и дисперсию величин U и V, а также определить коэффициент корреляции
№9,1
Решение:
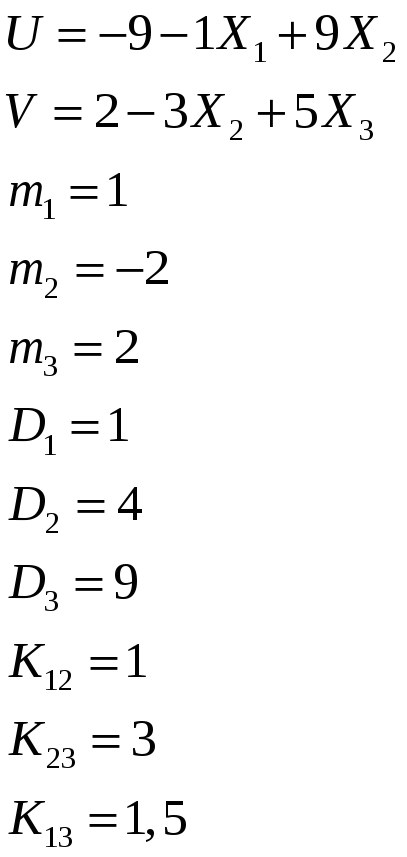
Коэффициент корреляции найдем по формуле
![]()
Воспользуемся свойством математического ожидания
![]()
![]()
Дисперсия
![]()
![]()

Коэффициент корреляции
![]()
ЗАДАЧА 10.
По выборке одномерной случайной величины:
- получить вариационный ряд;
- построить на масштабно-координатной бумаге формата А4 график эмпирической функции распределения F*(x);
- построить гистограмму равноинтервальным способом;
- построить гистограмму равновероятностным способом;
- вычислить точечные оценки математического ожидания и дисперсии;
- вычислить интервальные оценки математического ожидания и дисперсии (γ = 0,95);
- выдвинуть гипотезу о законе распределения случайной величины и проверить ее при помощи критерия согласия 2 и критерия Колмогорова ( = 0,05).
№10,32
Вариационный ряд
|
0,19 |
3,79 |
|
1,32 |
3,83 |
|
1,58 |
3,86 |
|
1,6 |
3,93 |
|
1,67 |
3,94 |
|
1,68 |
3,97 |
|
1,7 |
4,01 |
|
1,82 |
4,01 |
|
1,98 |
4,02 |
|
2,13 |
4,02 |
|
2,17 |
4,07 |
|
2,22 |
4,17 |
|
2,31 |
4,18 |
|
2,31 |
4,24 |
|
2,51 |
4,29 |
|
2,53 |
4,30 |
|
2,53 |
4,35 |
|
2,53 |
4,37 |
|
2,58 |
4,39 |
|
2,65 |
4,40 |
|
2,7 |
4,41 |
|
2,7 |
4,48 |
|
2,78 |
4,51 |
|
2,78 |
4,52 |
|
2,88 |
4,54 |
|
2,9 |
4,60 |
|
2,96 |
4,64 |
|
3,01 |
4,66 |
|
3,01 |
4,82 |
|
3,04 |
4,89 |
|
3,04 |
4,95 |
|
3,07 |
4,96 |
|
3,1 |
5,02 |
|
3,12 |
5,04 |
|
3,14 |
5,05 |
|
3,22 |
5,05 |
|
3,27 |
5,10 |
|
3,27 |
5,27 |
|
3,32 |
5,38 |
|
3,41 |
5,38 |
|
3,41 |
5,44 |
|
3,48 |
5,45 |
|
3,49 |
5,47 |
|
3,52 |
5,47 |
|
3,57 |
5,48 |
|
3,63 |
5,53 |
|
3,65 |
5,67 |
|
3,69 |
5,97 |
|
3,73 |
6,11 |
|
3,74 |
6,86 |
Эмпирическая функция распределения
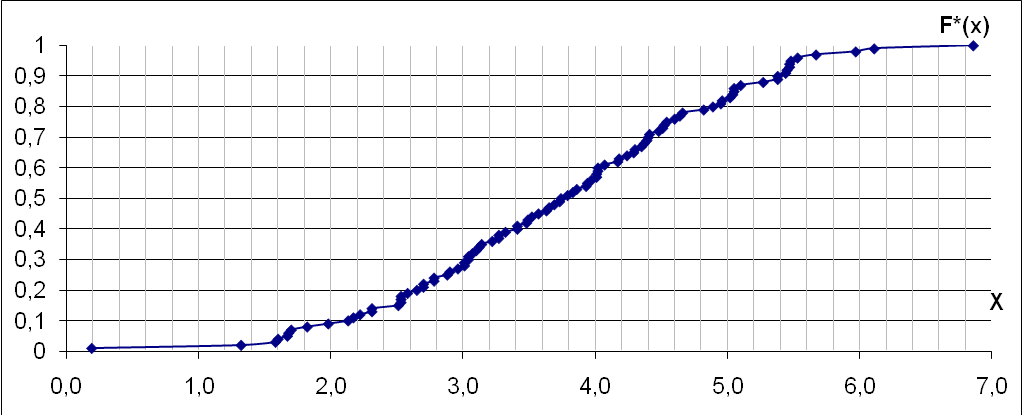
Разобьем множество значений на 10 интервалов
Шаг интервала
h=![]()
h=(6,86-0,19)/10=0,667
|
|
|
|
|
|
|
|
|
0,190 |
0,857 |
0,667 |
1 |
0,01 |
0,010 |
0,01 |
|
0,857 |
1,524 |
0,667 |
1 |
0,01 |
0,015 |
0,02 |
|
1,524 |
2,191 |
0,667 |
9 |
0,09 |
0,135 |
0,11 |
|
2,191 |
2,858 |
0,667 |
13 |
0,13 |
0,195 |
0,24 |
|
2,858 |
3,525 |
0,667 |
20 |
0,2 |
0,300 |
0,44 |
|
3,525 |
4,192 |
0,667 |
19 |
0,19 |
0,285 |
0,63 |
|
4,192 |
4,859 |
0,667 |
16 |
0,16 |
0,240 |
0,79 |
|
4,859 |
5,526 |
0,667 |
16 |
0,16 |
0,240 |
0,95 |
|
5,526 |
6,193 |
0,667 |
4 |
0,04 |
0,060 |
0,99 |
|
6,193 |
6,860 |
0,667 |
1 |
0,01 |
0,015 |
1,00 |
Гистограмма равноинтервальным способом
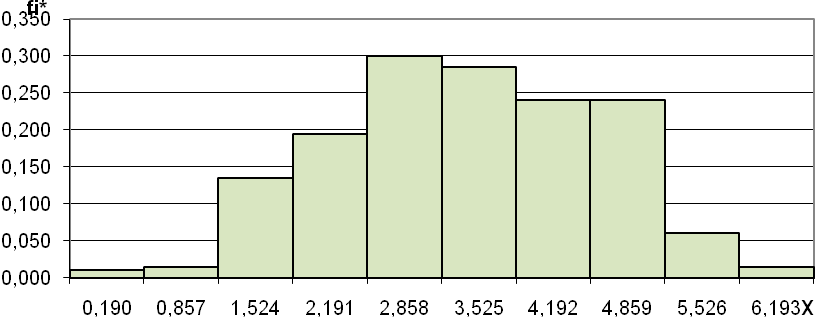
Гистограмма равновероятностным способом
|
|
|
|
|
|
|
|
0,190 |
0,857 |
1,98 |
10 |
0,1 |
0,051 |
|
0,857 |
1,524 |
0,53 |
10 |
0,1 |
0,189 |
|
1,524 |
2,191 |
0,34 |
10 |
0,1 |
0,294 |
|
2,191 |
2,858 |
0,37 |
10 |
0,1 |
0,270 |
|
2,858 |
3,525 |
0,38 |
10 |
0,1 |
0,263 |
|
3,525 |
4,192 |
0,28 |
10 |
0,1 |
0,357 |
|
4,192 |
4,859 |
0,34 |
10 |
0,1 |
0,294 |
|
4,859 |
5,526 |
0,54 |
10 |
0,1 |
0,185 |
|
5,526 |
6,193 |
0,49 |
10 |
0,1 |
0,204 |
|
6,193 |
6,860 |
1,42 |
10 |
0,1 |
0,070 |

Прямоугольники равновероятнстной гистограммы должны иметь одинаковую площадь!
Точечная оценка математического ожидания
![]() ,
где Хi
–
середина i-го
интервала
,
где Хi
–
середина i-го
интервала
Точечная оценка дисперсии
![]()
