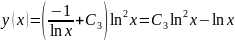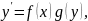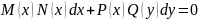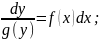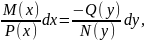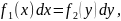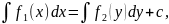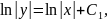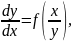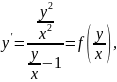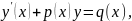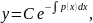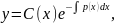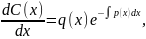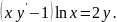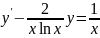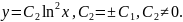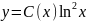1.3. Дифференциальные уравнения с разделяющимися переменными и приводящиеся к ним.

Определение 12. Дифференциальные уравнения вида:

(3.1)

или в дифференциалах:

(3.2)

называются дифференциальным уравнениями с разделяющимися переменными. Функции f, М, N. P. Q будем предполагать непрерывными.

Для решения (3.1) и (3.2) нужно обе части этих уравнений домножить или разделить на такие выражения, чтобы в одну часть получившегося равенства вошла только независимая переменная 𝑥, а в другую - только 𝑦.

В случае (3.1) умножим обе части на 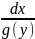и получим:

(3.3)

в случае (3.2) перепишем уравнение в виде М(𝑥)N(𝑦)𝑥 = -P(𝑥)Q(𝑦)d𝑦 и умножим обе части на 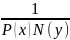, – в результате получим:

(3.4)

В дифференциальных уравнениях (3.3) и (3.4) переменные разделились. Таким образом, мы привели уравнения (3.1) и (3.2) к виду:

(3.5)

Если 𝑦(𝑥) - решение (3.5), то при подстановке 𝑦(𝑥) в (3.5) получим тождество

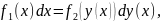
проинтегрируем обе части по переменной 𝑥. Имеем:

(3.6)

Каждое решение уравнения (3.6) удовлетворяет (3.5).

(Действительно, пусть 𝑦(𝑥) - решение (З.6) ⇒ при подстановке 𝑦(𝑥) в (3.6) получим тождество, дифференцируем обе его части по 𝑥 - получим (3.5) ⇒ 𝑦(𝑥) - решение (3.5)).

Пример 6. Проинтегрировать дифференциальное уравнение:

Перепишем его в виде:

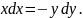
Переменные разделились, - интегрируем обе части и получаем:

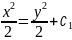
или

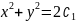
где ∁₁ принимает любые вещественные значения.

Обозначим 2∁₁ = С₂, тогда 𝑥² + 𝑦² = ∁₂, ∁₂ - любое вещественное. Интегральные кривые представляют собой семейство окружностей с центром в точке О(0,0) (см. пример 5).

Замечание 2. При переходе от (3.1) к (3.3) и от (3.2) к (3.4) мы делим на некоторые функции, - могут быть потеряны решения.

Пример 7. Проинтегрировать дифференциальное уравнение:

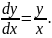
Разделяем переменные:

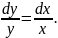
Интегрируем обе части:

(3.7)

затем потенцируем: 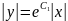и , (обозначив 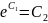, получаем .

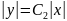Снимем знак абсолютной величины: 𝑦=±С₂𝑥. Обозначив ±С₂=С₃, получим 𝑦=С₃𝑥.

В (3.7) С₁ - любое вещественное ⇒ 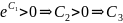- любое вещественное, кроме С₃=0.

Итак, 𝑦 = С₃𝑥, где С₃≠0.

При разделении переменных делили на 𝑦: могло быть потеряно решение 𝑦≡0. Подставим 𝑦=0 в исходное уравнение и получаем тождество, следовательно, 𝑦≡0 решение. Поэтому ответ: 𝑦 = С₃𝑥, где С₃≠0 и линия 𝑦≡0.

Можно записать этот ответ одной формулой 𝑦=С𝑥, С - любое вещественное.

(При С=0 формула 𝑦=С𝑥 даст и потерянное решение 𝑦≡0).

Определение 13. Дифференциальные уравнения вида:

(3.8)

называются однородными дифференциальными уравнениями.

Замена 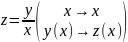приводит однородное дифференциальное уравнение͏͏͏͏͏ (3.8) к уравнению с разделяющимися переменными. Действительно, если 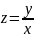, то 𝑦=z𝑥 и 𝑦'=z'𝑥+z.

Имеем 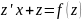или

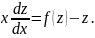
Делим обе части на :

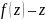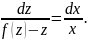
– переменные разделились.

Пример 8. Проинтегрировать дифференциальное уравнение:

(3.9)

Разделим обе его части на 𝑥² и получим:

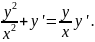
Откуда:

(3.10)

уравнение (3.10) - однородное.

Делаем замену 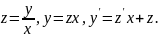Подставляем 𝑦 и 𝑦'в уравнение (3.10):

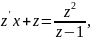
далее

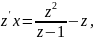
или

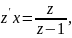
Разделяем переменные

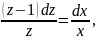
и интегрируем обе части

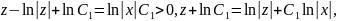
Потенцируем ,

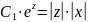Вернемся к старым переменным:

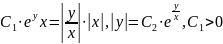
Снимаем знак абсолютной величины:

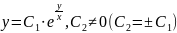
Ищем потерянные решения.

Делили на z–1, 𝑥, z.

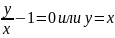1. . Подставим 𝑦=𝑥 в исходное уравнение: 𝑥² + 𝑥² ,

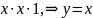не является решением;

2) 𝑥 = 0 поставляем в исходное уравнение, – 𝑥 = 0 не является решением;

3) z = 0, то есть 𝑦 = 0. Подставляем 𝑦 = 0 в исходное уравнение, получаем тождество, - это означает, что у = 0 - решение.

Итак,

или

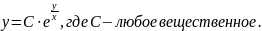
Определение 14. Линейным дифференциальным уравнением первого порядка называется дифференциальное уравнение, линейное относительно неизвестной функции 𝑦(𝑥) и ее производной 𝑦'(𝑥), то есть уравнение вида:

(3.11)

Функции p(x) и q(x) считаем непрерывными в той области G(x, 𝑦), в которой рассматривается (3.11).

Рассмотрим сначала линейное уравнение c q(x)≡0:

(3.12)

Уравнение (3.12) называется однородным, соответствующим дифференциальному уравнению (3.11).

Уравнение (3.12) - с разделяющимися переменными, проинтегрируем его:

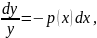
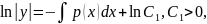
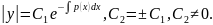
При делении на 𝑦 теряем решение равнения (3.12) 𝑦 ≡ 0, решение (3.12) имеет вид:

(3.13)

С - произвольное действительное число.

(при С=0 формула (3.13) даёт и потерянное речение 𝑦≡0).

Для нахождения решения (3.11) применим так называемый метод вариации произвольной постоянной, который заключается в следующем. Решение (3.11) ищем в виде, аналогичном (3.13):

(3.14)

считая С(x) некоторой неизвестной функцией от x.

Подставим (3.14) в (3.11) и получим:

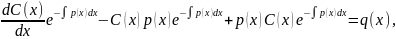
Отсюда:

(3.15)

Интегрируем (3.15) и находим:

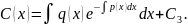
тогда

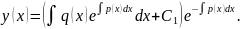
Пример 9. Проинтегрировать уравнение:

(3.16)

Перепишем (3.16) в виде:

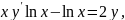
и далее

(*)

- линейное вида (3.11).

Решаем соответствующее однородное:

(3.17)

или

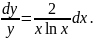
Интегрируем обе части:

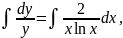
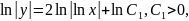
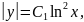
(3.18)

Для (3.17) 𝑦≡0 - потерянное решение ⟹ все решения (3.17) даются формулой , где C - любое действительное число. (при С=0 и потерянное решение 𝑦 ≡ 0 входит в (3.18).

Решение (*) ищем в виде:

(3.19)

Подставляем (3.19) в (*):

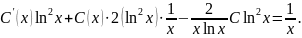
Отсюда

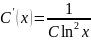и .

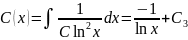Тогда