2.3. Метод интегрирования по частям

Например, требуется найти интеграл . Подынтегральная функция представляет собой произведение двух сомножителей. К сожалению, не существует формулы, выражающей интеграл от произведения функций через интегралы сомножителей. С этим связано то обстоятельство, что в отличие от производной интеграл от элементарной функции не всегда является элементарной функцией.

Пусть и  функции, имеющие непрерывные производные. Тогда . Интегрируя это равенство, получаем

или

. (2.2)

Формула (2.2) называется формулой интегрирования по частям. Она дает возможность свести вычисление интеграла к вычислению интеграла , который может оказаться существенно более простым, чем исходный.

Интегрирование по частям состоит в том, что подынтегральное выражение заданного интеграла представляется каким-либо образом в виде произведения двух сомножителей и (это, как правило, можно осуществить несколькими способами); затем, после нахождения и , используется формула интегрирования по частям. Иногда эту формулу приходится использовать несколько раз.

Большая часть интегралов, берущихся по формуле (2.2), может быть разбита на три группы:

1 группа. Интегралы вида , , , где  многочлен, - число. Удобно положить , а за обозначить все остальные сомножители.

2 группа. Интегралы вида , , , , . Удобно положить , а за обозначить остальные сомножители.

3 группа. Интегралы вида , , где и - числа, , . Применяя формулу (2.2) к любому из указанных интегралов дважды, мы получим для нахождения интеграла уравнение первого порядка, причем за можно принимать любой из сомножителей.

Конечно, указанные группы не исчерпывают всех интегралов, которые можно вычислять по формуле (2.2).

Пример 2.3. Найти следующие интегралы:

1)

;

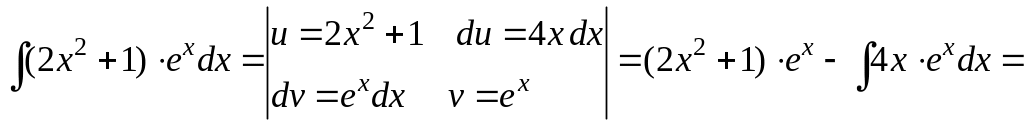
2)

;

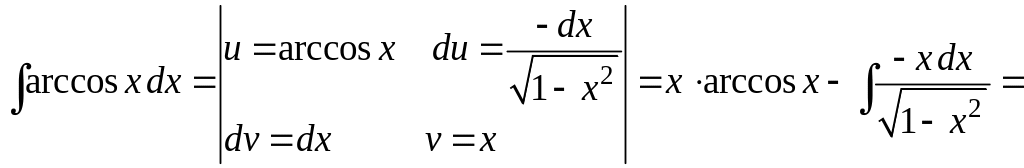
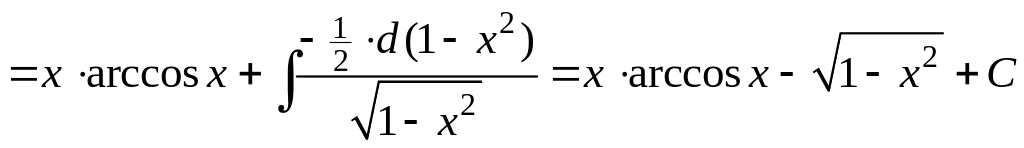3)

.

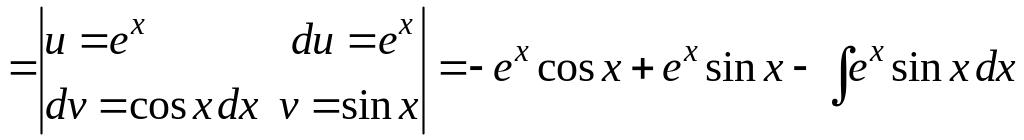Таким образом, получаем

.

Далее

,

.



3. Интегрирование рациональных,

ТРИГОНОМЕТРИЧЕСКИХ И ИРРАЦИОНАЛЬНЫХ

ФУНКЦИЙ

3.1. Понятия о рациональной функции

3.1.1. Многочлен

Функция вида

, (3.1)

где  натуральное число,  постоянные коэффициенты, называется многочленом (или целой рациональной функцией). Число называется степенью многочлена.

Корнем многочлена называется такое значение переменной , при котором многочлен обращается в нуль, т.е. .

Теорема 3.1. Если  корень многочлена , то многочлен делится без остатка на , т.е.

,

где  многочлен степени .

Возникает вопрос: всякий ли многочлен имеет корень? Положительный ответ на этот вопрос дает следующее утверждение, которое примем без доказательства.

Теорема 3.2 (основная теорема алгебры). Всякий многочлен

-ой степени имеет по крайней мере один корень, действительный или комплексный.

Теорема 3.3. Всякий многочлен можно представить в виде

, (3.2)

где  корни многочлена,  коэффициент многочлена при .

Например, следующие многочлены можно представить в виде произведения линейных множителей:

1) ;

2) .

Если в разложении многочлена (3.2) какой-либо корень встречается раз, то он называется корнем кратности . В случае (т.е. корень встречается один раз) корень называется простым.

Разложение многочлена (3.2) можно записать в виде

,

если корень имеет кратность , корень  кратность и так далее. При этом , а  число различных корней.

Рассмотрим следующие утверждения, которые примем без доказательства.

Теорема 3.4. Если два многочлена равны друг другу, то коэффициенты одного многочлена равны соответственно коэффициентам другого.

Например, если , то .

Теорема 3.5. Если многочлен с действительными коэффициентами имеет комплексный корень , то он имеет и сопряженный корень .

В разложении многочлена (3.2) комплексные корни входят сопряженными парами. Действительно, перемножив линейные множители

,

где , получаем трехчлен второй степени с действительными коэффициентами.

Таким образом, произведение линейных множителей, соответствующих сопряженным корням, можно заменить квадратным трехчленом с действительными коэффициентами.

С учетом вышеизложенного справедлив следующий факт.

Теорема 3.6. Всякий многочлен с действительными коэффициентами разлагается на линейные и квадратные множители с действительными коэффициентами, т.е. многочлен можно представить в виде

. (3.3)

При этом , все квадратные трехчлены не имеют вещественных корней.

Например,

1) ;

2)

.