
- •Раздел 6
- •Повторение
- •1. Неопределенный интеграл
- •1.1. Первообразная функции. Неопределенный интеграл
- •1.2. Свойства неопределенного интеграла
- •1.3. Таблица основных неопределенных интегралов
- •2. Методы интегрирования
- •2.1. Метод непосредственного интегрирования
- •2.2. Метод интегрирования подстановкой (заменой переменной)
- •2.3. Метод интегрирования по частям
- •3. Интегрирование рациональных,
- •3.1. Понятия о рациональной функции
- •3.1.1. Многочлен
- •3.1.2. Дробно-рациональная функция
- •3.2. Интегрирование рациональных дробей
- •3.3. Интегрирование тригонометрических функций
- •3.3.1. Интегралы вида
- •3.3.2. Интегралы вида
- •3.4.2. Дробно-линейная подстановка
- •3.4.3. Тригонометрическая подстановка
- •3.4.4. Интегрирование дифференциального бинома
- •3.5. «Берущиеся» и «неберущиеся» интегралы
- •I. О технике интегрирования
- •II. Использование таблиц интегрирования
- •III. Об интегрировании в элементарных функциях
- •4. Определенный интеграл
- •4.1. Понятие определенного интеграла
- •Задача о площади криволинейной трапеции
- •Задача о работе переменой силы
- •4.2. Основные свойства определенного интеграла
- •4.3. Формула НьютонаЛейбница
- •4.4. Вычисление определенного интеграла
- •5. Несобственные интегралы
- •5.1. Интеграл с бесконечным промежутком интегрирования (несобственный интеграл первого рода)
- •5.2. Интеграл от разрывной функции (несобственный интеграл второго рода)
1.2. Свойства неопределенного интеграла
Отметим ряд свойств неопределенного интеграла, вытекающих из его определения. Некоторые свойства мы докажем.
Свойство 1. Дифференциал от неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции.
![]() ,
,
![]()
Доказательство. Действительно,
![]() ,
,
и
![]() .
.
Благодаря свойству 1 правильность интегрирования проверяется дифференцированием.
Свойство 2. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:
![]() .
.
Доказательство. Действительно,
![]()
Свойство 3. Постоянный множитель можно выносить за знак интеграла:
![]() .
.
Свойство 4. Неопределенный интеграл от алгебраической суммы конечного числа непрерывных функций равен алгебраической сумме интегралов от слагаемых функций:
![]() .
.
Свойство 5 (инвариантность формулы
интегрирования). Если
![]() ,
то и
,
то и
![]() ,
где
,
где
![]() произвольная
функция, имеющая непрерывную производную.
произвольная
функция, имеющая непрерывную производную.
Пример 1.1. Найти интеграл
![]() .
.
Решение.
![]() по
свойству 3=
по
свойству 3=![]() по
свойству 5=
по
свойству 5=![]() по
свойству 2=
по
свойству 2=![]() .
.
1.3. Таблица основных неопределенных интегралов
Пользуясь тем, что интегрирование есть действие, обратное дифференцированию, можно получить таблицу основных интегралов путем обращения соответствующих формул дифференциального исчисления и использование свойств неопределенного интеграла.
Интегралы в приводимой ниже таблице называются табличными. В интегральном исчислении нет простых и универсальных правил отыскания первообразных от элементарных функций, как в дифференциальном исчислении. Методы нахождения первообразных (т.е. интегрирования функций) сводятся к указанию приемов, приводящих данный (искомый) интеграл к табличному. Следовательно, необходимо знать табличные интегралы наизусть и уметь их узнавать.
Таблица основных интегралов
1.
![]() ;
11.
;
11.
![]() ;
;
2.
![]() ;
12.
;
12.
![]() ;
;
3.
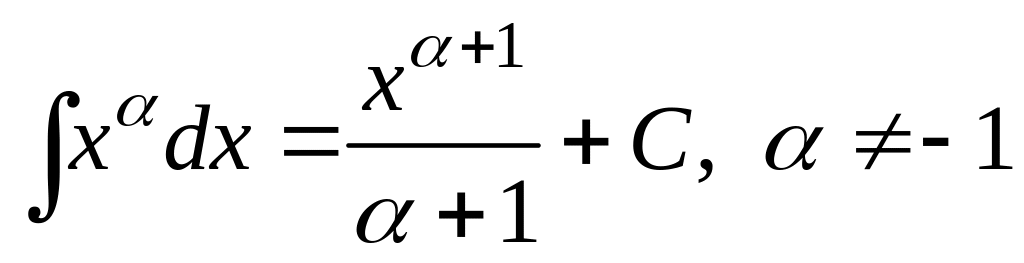 ;
13.
;
13.
![]() ;
;
4.
![]() ;
14.
;
14.
![]() ;
;
5
![]() ;
15.
;
15.
![]() ;
;
6.
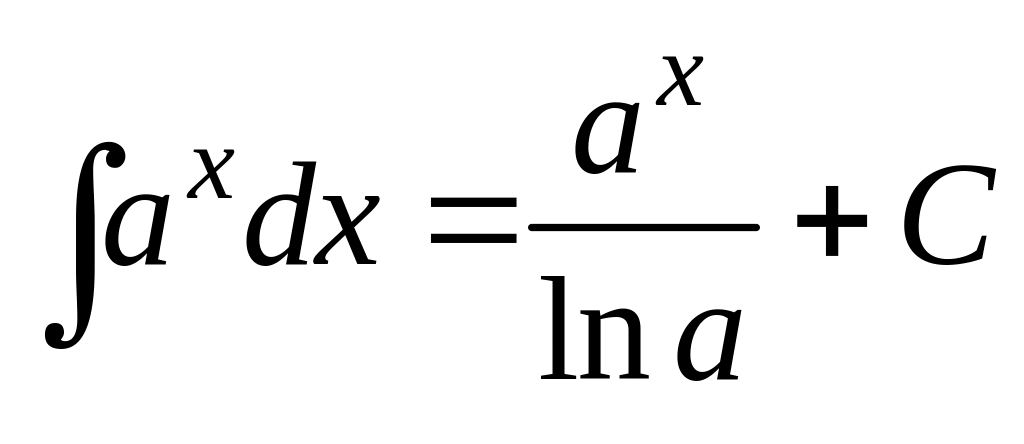 ;
16.
;
16.
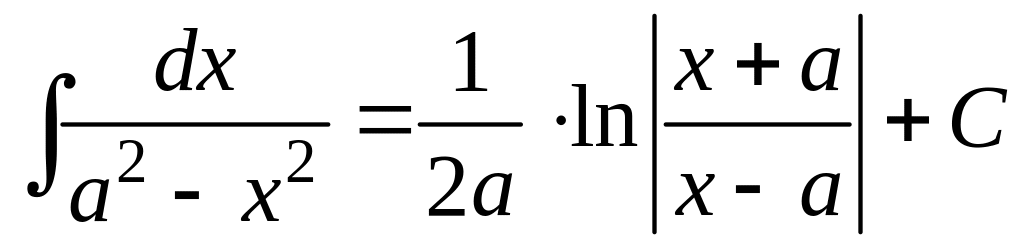 ;
;
7.
![]() ;
17.
;
17.
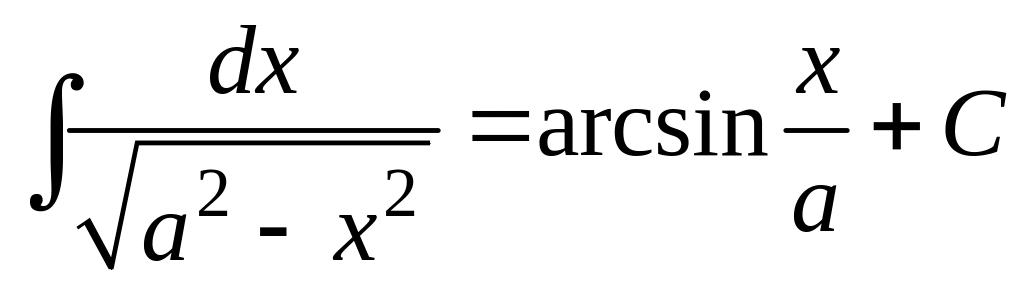 ;
;
8.
![]() ;
18.
;
18.
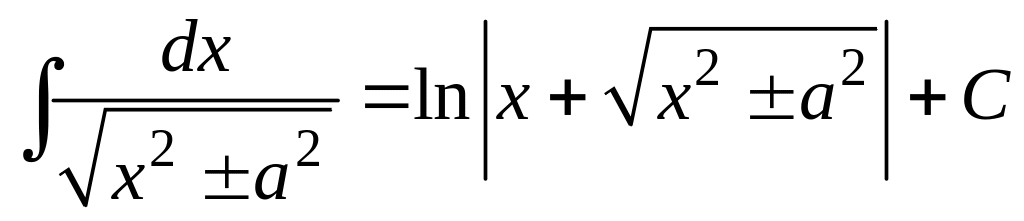 .
.
9.
![]() ;
;
10.
![]() ;
;
2. Методы интегрирования
2.1. Метод непосредственного интегрирования
Метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции (или выражения) и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием.
Пример 2.1. Найти следующие интегралы:
1)

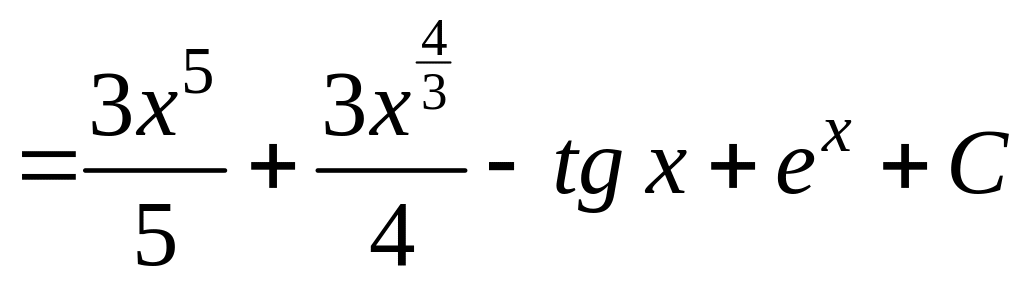 .
.
2)
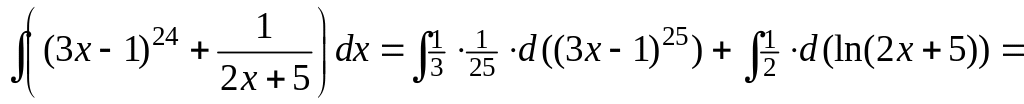
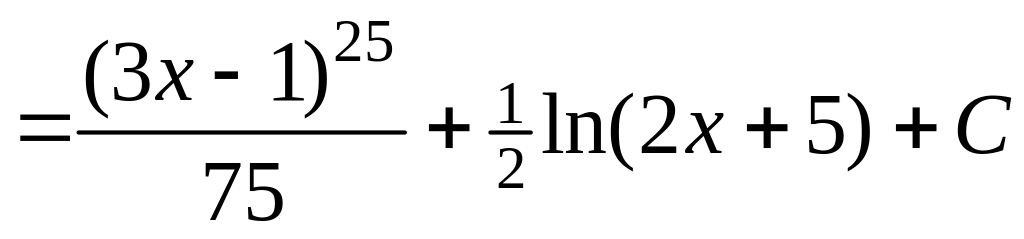 .
.
3)
 ;
;
4)
![]()
![]() .
.
2.2. Метод интегрирования подстановкой (заменой переменной)
Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (т.е. подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся (в случае «удачной» подстановки). Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.
Пусть требуется найти интеграл , причем непосредственно подобрать первообразную для мы не можем, но нам известно, что она существует.
Сделаем замену переменной в подынтегральном
выражении, положив
![]() ,
где
,
где
![]() непрерывная функция
с непрерывной производной, имеющая
обратную функцию. Тогда
непрерывная функция
с непрерывной производной, имеющая
обратную функцию. Тогда
![]() и на основании свойства инвариантности
формулы интегрирования неопределенного
интеграла получаем формулу
интегрирования подстановкой
и на основании свойства инвариантности
формулы интегрирования неопределенного
интеграла получаем формулу
интегрирования подстановкой
![]() .
(2.1)
.
(2.1)
Иногда целесообразно подбирать
подстановку в виде
![]() ,
тогда
,
тогда
![]() ,
где
.
,
где
.
Другими словами, формулу (2.1) можно применять справа налево.
Пример 2.2. Найти следующие интегралы:
1)
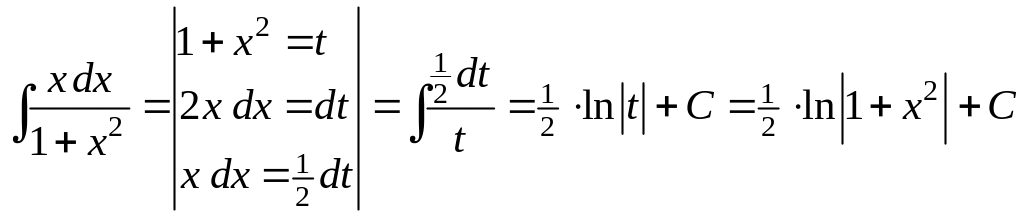 ;
;
2)
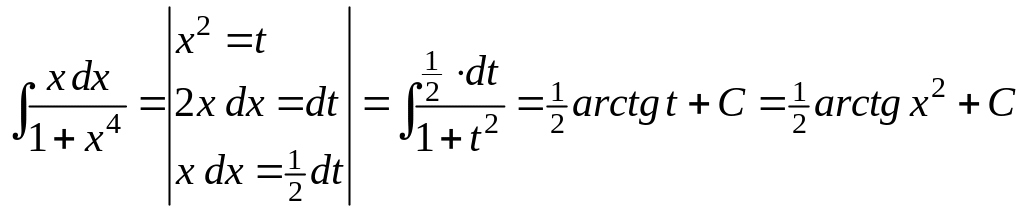 ;
;
3)
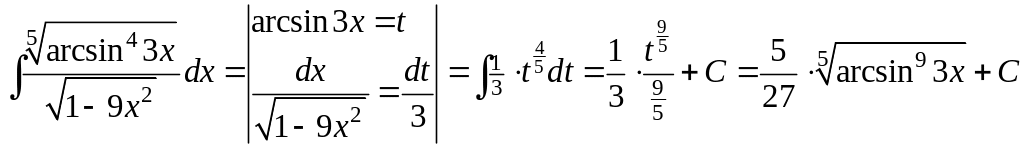 ;
;
4)
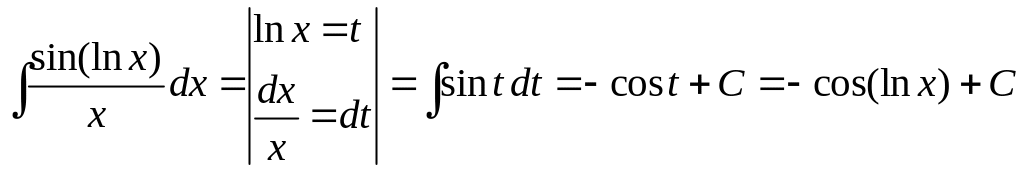 .
.
