Метод підстановки

Нехай для деякої фірми виробнича функція має вигляд:

Q = f(K,L) = 4L K + L² Нехай також витрати на одиницю капіталу і труда становлять 1 і 2 відповідно. Необхідно з’ясувати рівень витрат на капітал і труд, коли випуск продукції максимальний, тобто знайти такі значення К і L , при яких функція Q досягає максимуму. Загальна сума витрат складає, згідно з умовою, 105, тому обмеження по витратам матимуть вигляд: K + 2L =105

Для розв’язку виразимо К через L. K = 105 - 2L Підставивши цей вираз в виробничу функцію замість K, отримаємо: Q = 4L(105 - 2L)+L² =420L - 7L² тобто матимемо цільову функцію однієї змінної. В цьому і полягає основна ідея методу підстановки. Далі традиційним методом дослідимо отриману функцію на максимум.

Обчислимо похідну виробничої функції і прирівнявши її до нуля знайдемо стаціонарні точки.

QL=420 - 14L=0 ; звідси L=30;

Обчислимо другу похідну і з‘ясуємо її знак Q= - 14 <0 це означає, що в стаціонарній точці матимемо максимум.

І остаточно підставивши значення стаціонарної точки в цільову функцію, залежну тільки від L , визначимо максимальний випуск продукції: Q=420  30 - 7 30² =6300

Відповідні витрати на капітал визначаються підстановкою оптимальної величини в обмеження по витратам:

K=105 - 2L=105 - 2  30=45

В загальному випадку для знаходження умовного екстремуму довільної цільової функції z = f(x; y), при умові ( обмеженні )

g(x; y) = 0, також можна застосовувати метод підстановки. Для цього перш за все, використовуючи обмеження виражаємо змінну у через x, y = h(x). Підставляючи в цільову функцію h ,отримаємо деяку функцію однієї змінної: z = f(x; h(x)) = F(x) А далі вже знаходимо екстремальні точки для цієї функції. По знайденим значенням х використовуючи функцію y = h(x) ,обчислимо відповідні екстремальні значення у.

Нажаль неявну функцію g(x; y) = 0, що виражає обмеження задачі оптимізації часто буває важко, а іноді і неможливо виразити явною. У цих випадках необхідно використовувати інші методи розв’язання, один з яких так званий метод множників Лагранжа.

Метод множників Лагранжа.

Якщо необхідно знайти умовний екстремум цільової функції

z = f(x; y), при обмеженні g(x; y) = 0, то метод Лагранжа полягає в такому алгоритмі:

1. Вводиться нова функція трьох змінних

F(x ,y ,) = f(x; y) + g(x; y) , де  - невизначений множник, який розглядається як нова змінна.

2. Обчислюємо екстремум (уже безумовний)цієї нової функції. Для цього обчислюємо частинні похідні першого порядку і прирівнюємо їх до нуля:

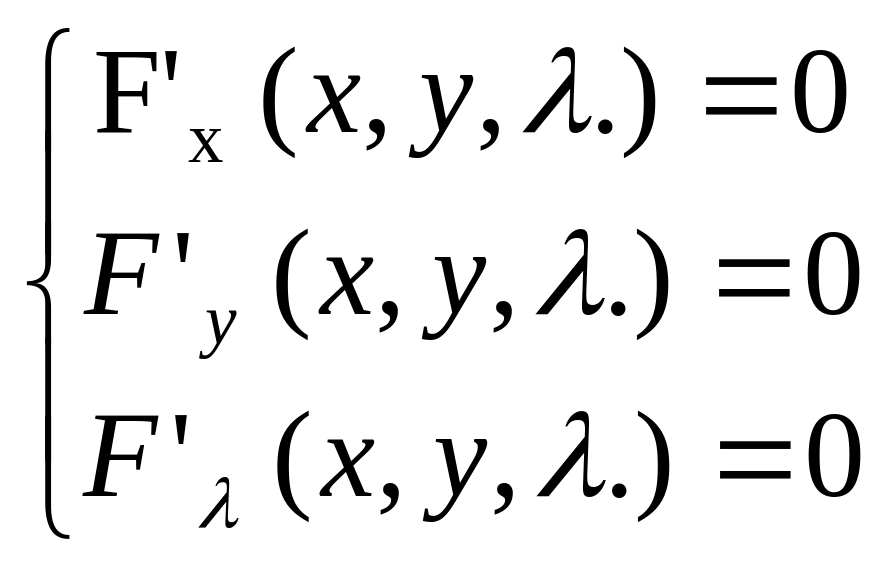
3. Розв’язуємо отриману систему рівнянь відносно х; у;  . В отриманому розв’язку перші два значення (х₀; у₀) відповідають значенню умовного екстремуму вихідної функції z = f(x; y).

Приклад 1 . Знайти екстремум функції f(x; y)= x² - 3xy + 12x при умові: g(x; y) = 6 -2x -3y = 0

Розв’язання

Будуємо допоміжну функцію F(x; y;)= x² - 3xy + 12x+(6 -2x -3y)

і обчислюємо частинні похідні F_x(x, y,)=2x -3y+12 -2

F_y(x, y,)= -3x -3

F_(x, y,)=6 -2x -3y

Прирівнявши визначені частинні похідні до нуля і виконавши елементарні перетворення отримаємо систему:

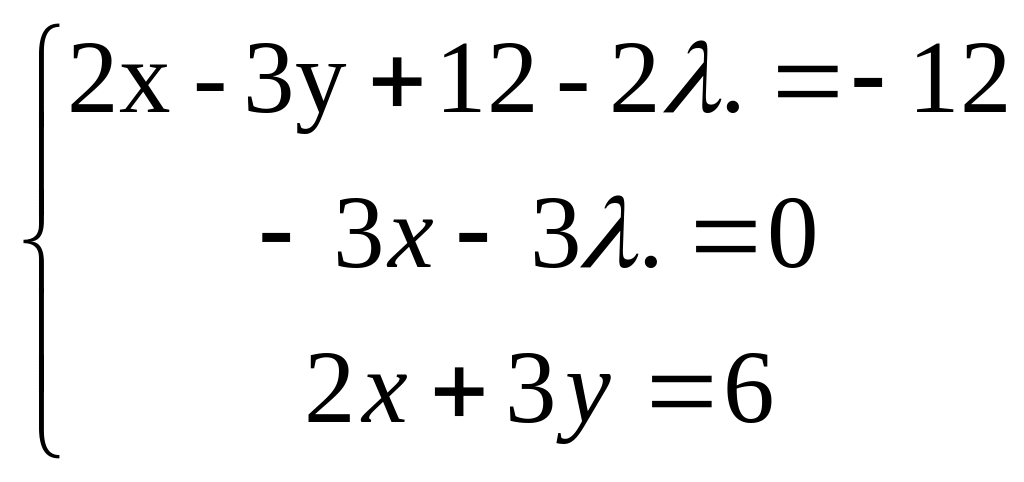
Застосувавши метод Ж - Гаусса знайдемо її корені:x=-1;y=8/3; =1

Значення цільової функції f(-1;8/3) = ( -1)² -3(-1 (8/3)+12 (-1) = -3

Приклад 2. Фірма монополіст виробляє два вида товарів G₁ i G₂ відповідно у кількостi Q₁ i Q₂. Функція витрат має вигляд, C = 10Q₁ + Q₁Q₂ + 10Q₂ , а криві попиту для кожного виду товарів P₁ =50 - Q₁ + Q_{2 ;} P₂ =30+2Q₁ - Q₂, де P₁ і P₂ - ціни одиниці відповідно товарів G₁ i G₂ . Крім того фірма обмежена по загальному об’єму виробництва товарів G₁ i G₂ її квота становить 15 одиниць, тобто Q₁ + Q₂ = 15 Необхідно знайти максимальний прибуток, який можна досягти при такому обмеженні.

Розв’язання

Побудуємо цільову функцію, в даному випадку функції прибутку, який визначається як різниця між доходом та витратами S = R - C

Для доходу від продажу товару G₁ , матимемо:

R₁ =P₁ Q₁ = (50 - Q₁ + Q₂ )Q₁ = 50Q₁ - Q₁² - Q₁Q₂

Аналогічно доход від продажу товару G₂ :

R₂ = P₂ Q₂ = (30+2Q₁ - Q₂) Q₂ =30Q₂ +2Q₁ Q₂ - Q₂²

Очевидно, що сумарний доход становитиме :

R = R₁ + R₂ = 50Q₁ - Q₁² +3Q₁Q₂ +30Q₂ - Q₂²

Оскільки витрати відомі з умови задачі, то прибуток ( цільова функція) матиме вигляд:

s(Q₁;Q₂)=R–C=(50Q₁- Q₁²+3Q₁Q₂ +30Q₂ -Q₂²)- (10Q₁+ Q₁Q₂ +10Q₂₎ = =40Q₁ - Q₁² +2 Q₁Q₂ +20Q₂ - Q₂²

Врахуємо дані за умовою задачі обмеження g( Q₁; Q₂)=15-Q₁-Q₂ = 0

і застосуємо для розв’язку задачі метод Лагранжа

1. Будуємо допоміжну функцію

F(Q₁; Q₂;)= 40Q₁ - Q₁² +2 Q₁Q₂ +20Q₂ - Q₂²+(15 -Q₁ -Q₂)

2. Обчислюємо частинні похідні та прирівнюємо їх до нуля:

F_Q1 = 40 - 2 Q₁ +2Q₂ -=0

F_Q2 = 2 Q₁ +20 -2Q₂ -=0

F_ =15 -Q₁ -Q₂=0

3. Розв’язуємо отриману систему рівнянь за методом Ж - Гаусса

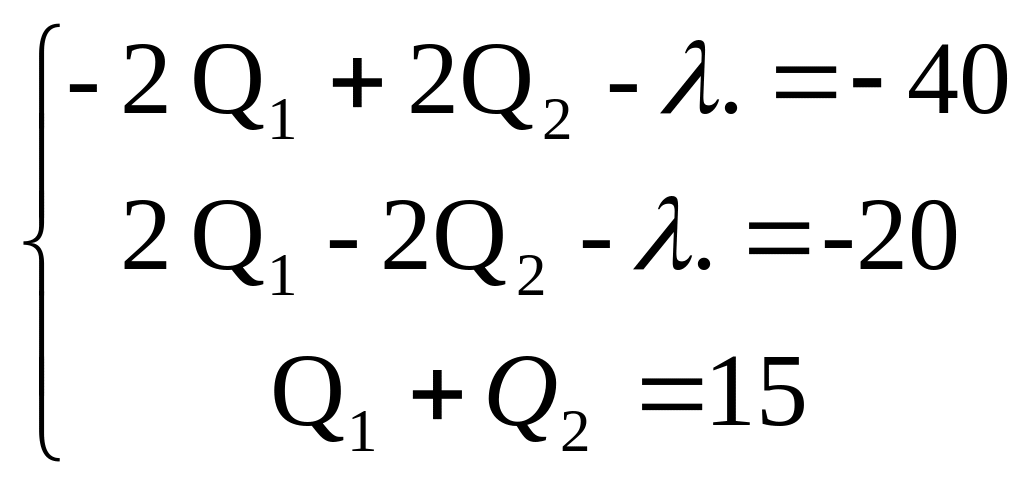
отримаємо: Q₁ =10; Q₂=5; =30;

Точка(Q₁; Q₂) =(10;5) - точка максимуму прибутку. Відповідне значення самого прибутку становитиме:

s(10;5)=4010 - 10²+2 10 5+20 5 -5² = 475

Зауваження: В наш час існує велика кількість програмних пакетів, що дозволяють численно розв’язувати задачі як безумовної так і умовної оптимізації. Однак для ефективного використання цих засобів необхідно мати чітке уявлення про основні поняття та можливості оптимізації.