Задания к главе 4 Тестовые примеры

Здесь приведены 10 примеров, которые могут быть использованы при предварительной отладке программ, составленных с применением различных численных методов решения задач на собственные значения.

1. Найти все собственные значения на основе классического метода Якоби:

А= . Ответ:

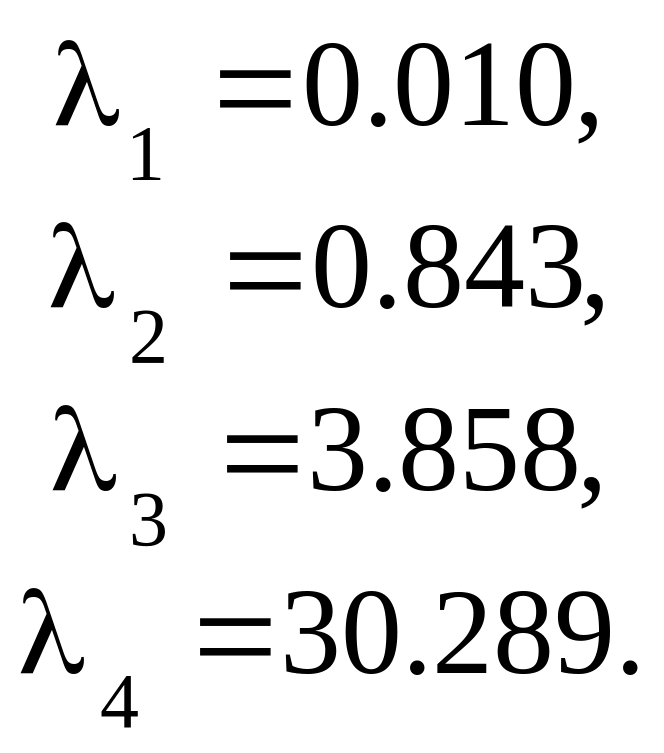
2. Найти все собственные значения на основе барьерного метода Якоби:

А= . Ответ:

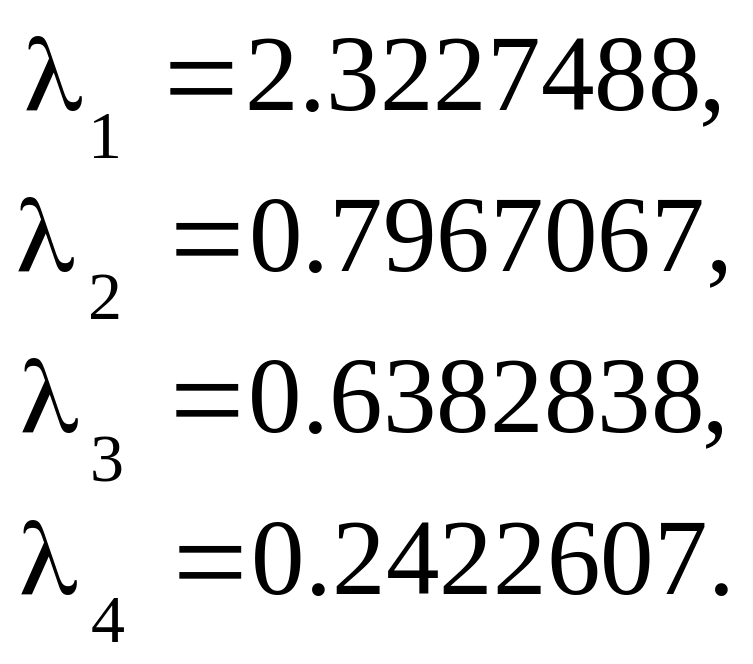
3. Найти все собственные значения с применением экономической стратегии выбора аннулируемого элемента:

А= . Ответ:

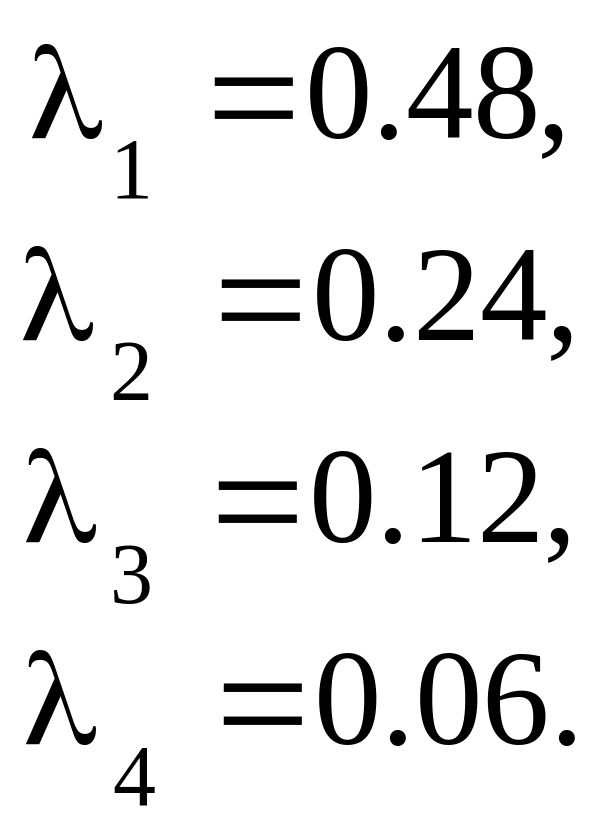
4. Найти все собственные значения и соответствующие им собственные вектора методом итерации:

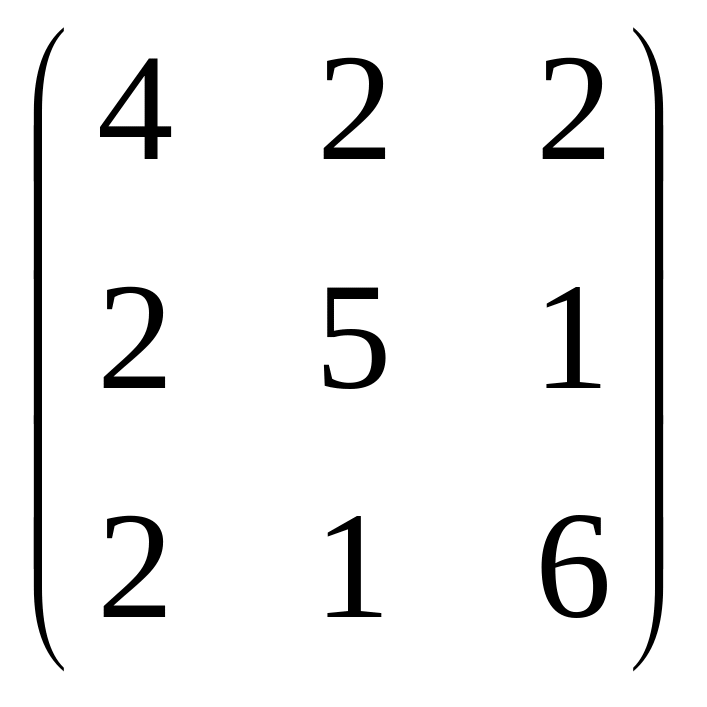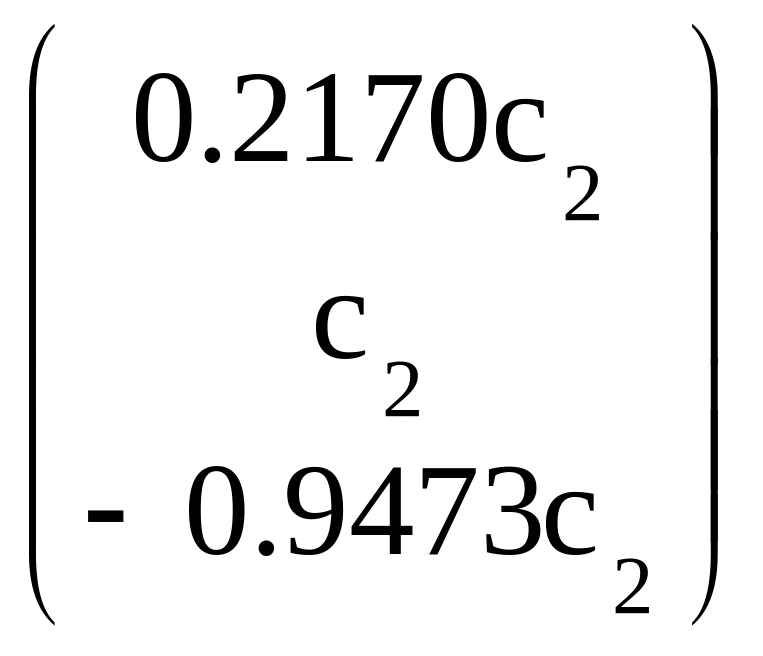А= . Ответ: х₁= , х₂= , х₃= ,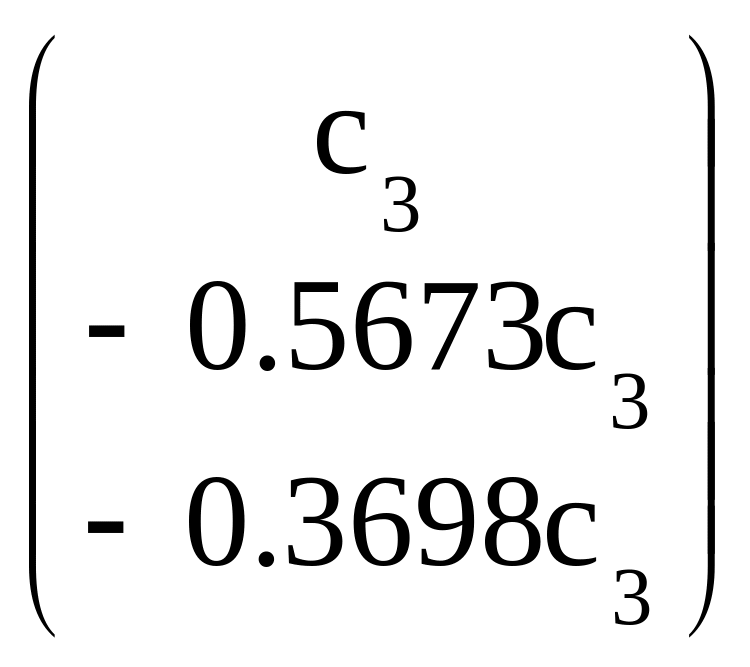

где с₁, с₂, с₃ – произвольные постоянные, отличные от нуля.

5. Найти максимальное по модулю собственное значение с применением степенного метода:

А= . Ответ: _max=2.3227488.

6. Найти минимальное по модулю собственное значение с применением обратного степенного метода:

А=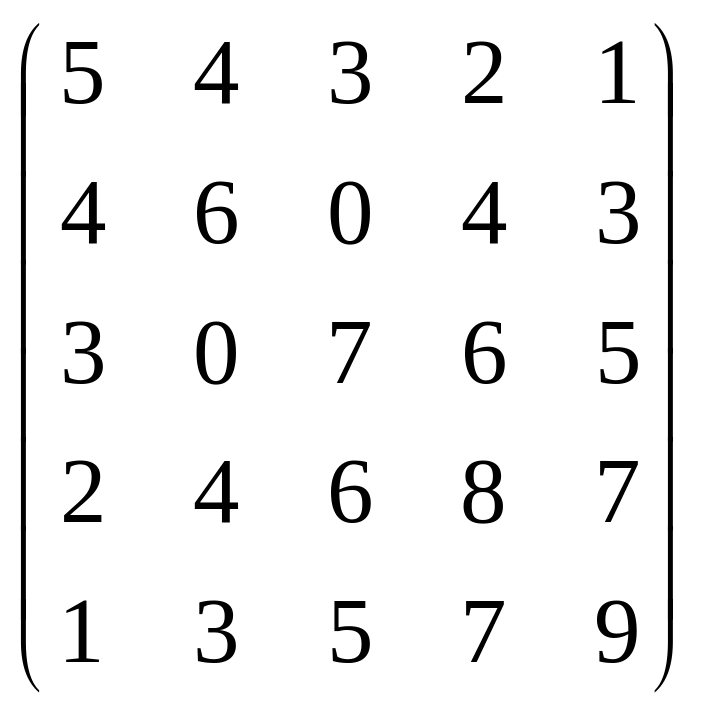 . Ответ: _min=-1.096595.

7. Найти минимальное по модулю собственное значение с применением обратного степенного метода со сдвигом:

А= .

Ответ: _min=0.24226071.

8. Найти все собственные значения с применением

QL – алгоритма:

А= .

Ответ: ₁=-17.86303, ₂=-17.15266, ₃=-7.57404, ₄=-5.2987.

9. Найти все собственные значения с применением

QR – алгоритма:

А= .

Ответ: ₁=1, ₂=2/3, ₃=4/9, ₄=1/3.

10. Решить обобщенную задачу на собственные значения:

А=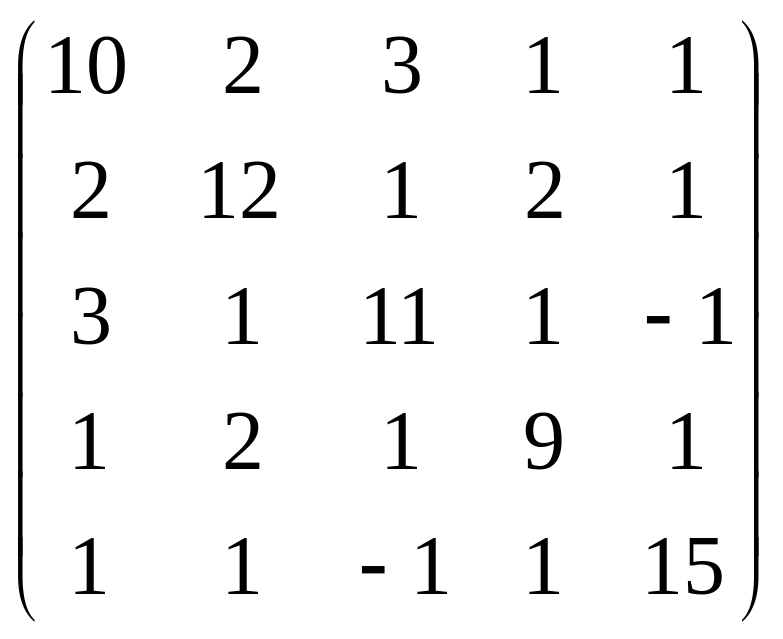 , В= .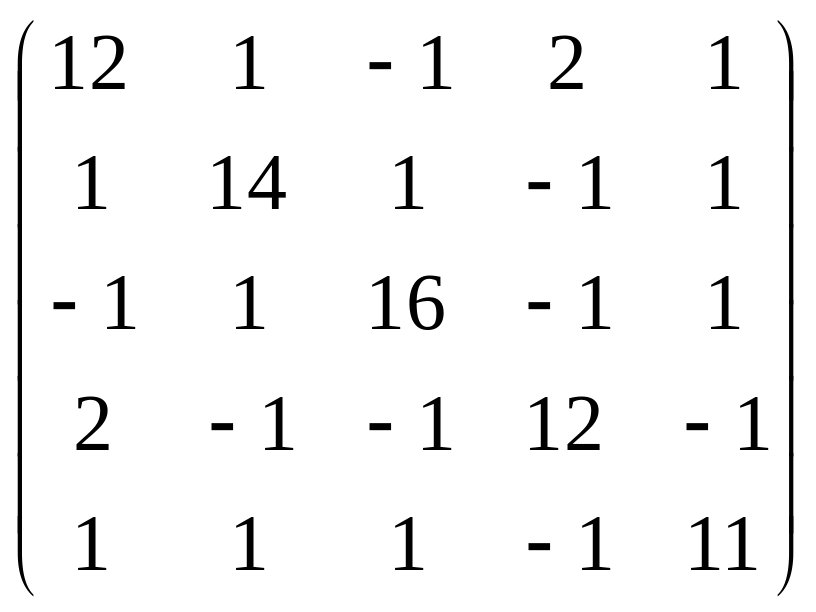

Ответ:

к	Ах=Вх	Вх=Ах
1	0.4327872	0.6700826
2	0.6636627	0.90148196
3	0.9438590	1.0594803
4	1.1092845	1.5067894
5	1.4923532	2.3106043

Задание для индивидуального выполнения

Ниже приводится задание, которое может принимать различные варианты. Варианты, в свою очередь, могут использоваться в качестве задания при реализации разных методов. Здесь , при b_i=0 и i=0 собственные значения матрицы A_i равны: 81, 9, -3, -6, -27, -54.

Различие вариантов достигается выбором i и b_i , например, b_i= . Тогда собственные значения матрицы A_i будут примерно равными: 81+i, 9+i, -3+i, -6+i, -27+i, -54+i.

A_i= .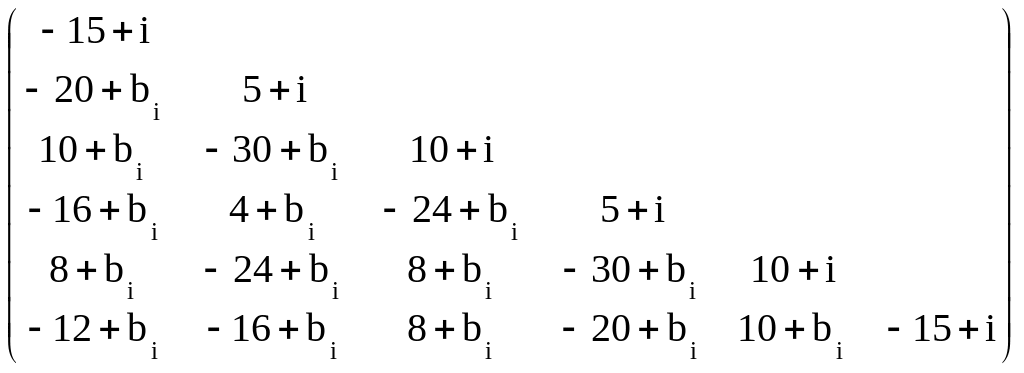

Литература

1. Гантмахер Ф.Р. Теория матриц. М., Наука, 1988, 548 с.

2. Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. Москва-Ленинград, Гос. Издат. Физико-математической литературы, 1963, 734 с.

3. Демидович Б.П., Марон И.А. Основы вычислительной математики. М., Наука, 1970, 664 с.

4. Крылов В.И., Бобков В.В., Монастырный П.И. Вычислительные методы. Том I. М., Наука, 1976, 303 с.

5. Воеводин В.В. Вычислительные основы линейной алгебры. М., Наука, 1977, 303 с.

6. Калиткин Н.Н. Численные методы. М., Наука, 1978, 512 с.

7. Стренг Г. Линейная алгебра и ее применения. М., Мир, 1980, 454 с.

8. Самарский А.А. Введение в численные методы. М., Наука, 1982, 271 с.

9. Коновалов А.Н. Введение в вычислительные методы линейной алгебры. Новосибирск, Наука, 1993, 158 с.

10. Рябенький В.С. Введение в вычислительную математику. М., Наука, 1994, 334 с.

11. Вержбицкий В.М. Численные методы (линейная алгебра и нелинейные уравнения). М., Высшая школа, 2000, 266 с.

12. Икрамов Х.Д. Несимметричная проблема собственных значений. М., Наука, 1991, 240 с.

13. Парлетт В. Симметричная проблема собственных значений. М., Мир, 1983, 382 с.

14. Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы для инженеров. М., Высшая школа, 1994.

15. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. М., Наука, 1987.

16. Самарский А.А., Гулин А.В. Численные методы. М., Наука, 1989.

17. Уилкинсон Дж.Х. Алебраическая проблема собственных значений. М., Наука, 1970.

18. Форсайт Дж., Молер К. Численное решение систем линейных алгебраических уравнений. М., Мир, 1969.

19. Воеводин В.В., Кузнецов Ю.А. Матрицы и вычисления. М., Наука, 1984.

20. Икрамов Х.Д. Численные методы для симметричных линейных систем. М., Наука, 1988.