4.2.1. Различные варианты метода Якоби

Классический метод. На каждой итерации классического метода Якоби зануляется максимальный по модулю недиагональный элемент с номером:

(i_n, j_n) , n=0, 1, 2,…

Барьерные методы. Используется простая циклическая последовательность аннулирования недиагональных элементов матрицы, т.е. элементы матрицы зануляются в следующем порядке: (2, 1), (3, 1), (3, 2),…, (n, 1), (n, 2),…, (n, n-1), а затем начинается новый проход по матрице в том же порядке. При этом вращения опускаются, если меньше некоторого барьерного значения , которое может быть фиксировано, а может меняться на каждой итерации.

Фиксированный барьер меняется, если все диагональные элементы стали меньше его следующим образом:

1. В качестве барьера  выбирается произвольное положительное число. Затем, когда все недиагональные элементы становятся по модулю меньше его, барьер заменяется на новый ^’=/const.

2. В качестве начального барьера выбирается 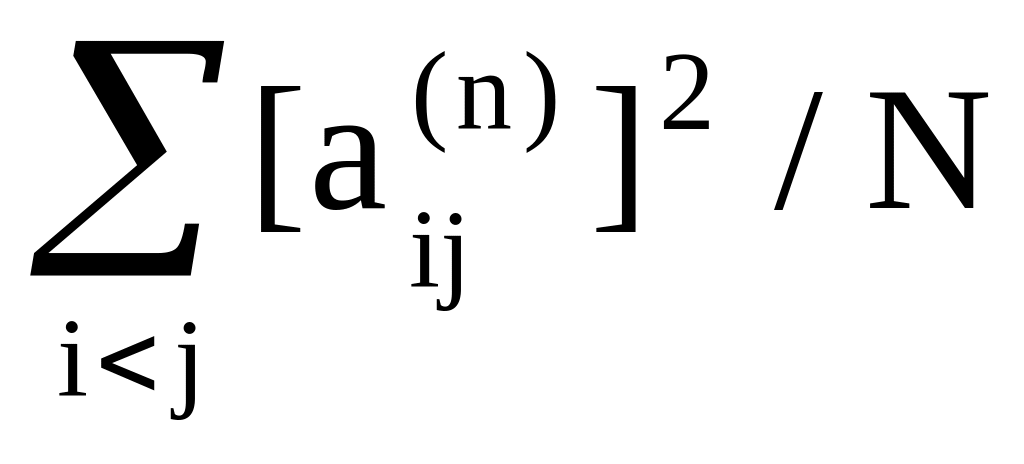= , где N – количество над диагональных элементов. Затем на каждой итерации величина 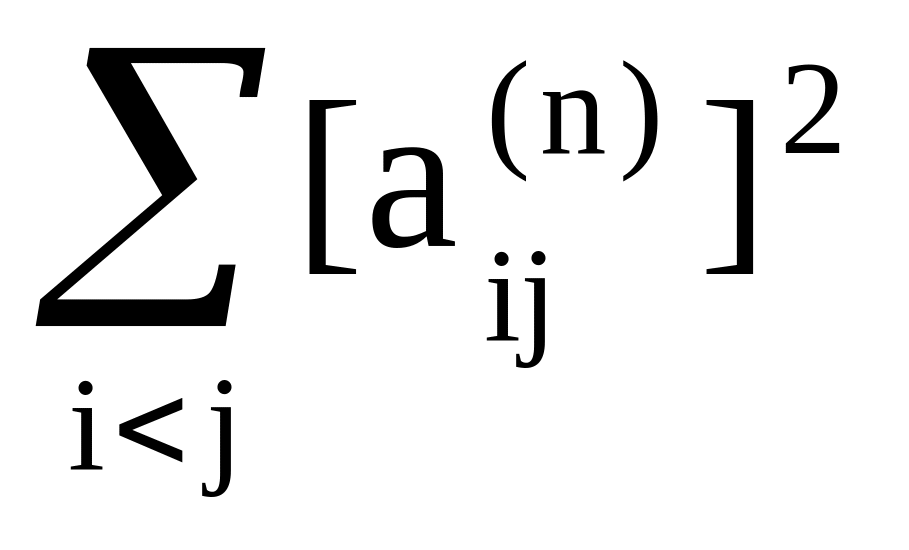уменьшается на 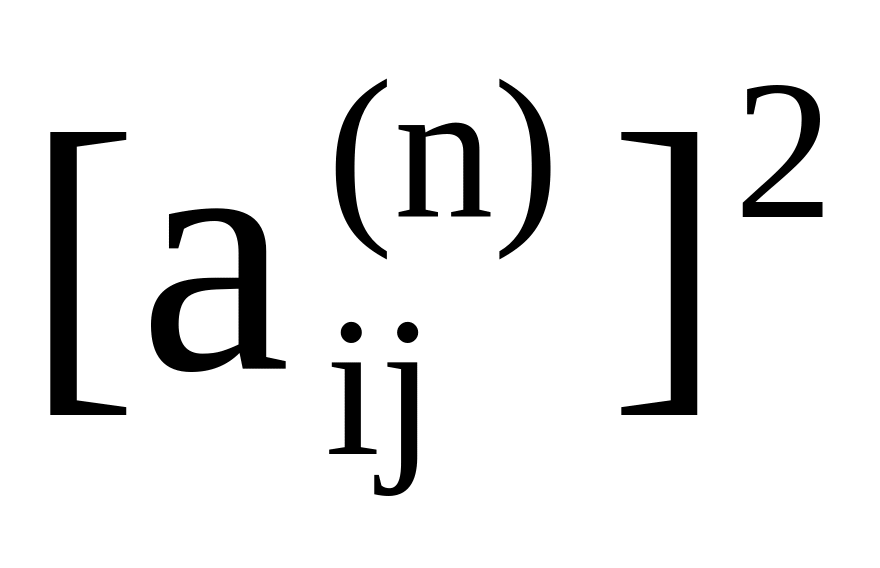и  перевычисляется по той же формуле.

3. Значения барьера выбираются так же как в пункте 2, но в качестве критерия проведения вращения используется условие N > , n=0,1,2,…

Экономическая стратегия выбора аннулируемого элемента. Выбор номера (i_k, j_k) зануляемого элемента матрицы происходит следующим образом:

а) вычисляются суммы внедиагональных элементов матрицы по строкам

S_i= ;

б) выбирается максимальная сумма

в) выбирается максимальный элемент, входящий в максимальную сумму

, k=0, 1, 2,…

4.3. Степенной метод

Степенной метод [2-4, 6, 9, 11, 12] предназначен для нахождения наибольшего по модулю собственного значения и соответствующего собственного вектора. Метод является простым, тем не менее, нечасто используется на практике из-за медленной сходимости. Знакомство с методом оправданно тем, что на его идее основаны более эффективные методы.

Пусть А=A^* и

₁<₂<…<_n-1<_n. (4.19)

Зададим произвольный вектор у₀ таким, что

(у₀, x_n)0

и образуем последовательность

y_k+1=Ay_k . (4.20)

Далее строим последовательность скалярных произведений

(y_k, y_k), (y_k+1, y_k), k=0, 1, 2,…

Покажем, что

= =_n (4.21)

или

=_n+О( ). (4.22)

Разложим вектор у₀ по собственным векторам матрицы А

y₀= ,

y₁=Ay₀= = ,

y₂=Ay₁= = ,

………………………………

y_k= ,

y_k+1= .

Тогда

(y_k, y_k)= ,

(y_k+1, y_k)= .

Значит

=

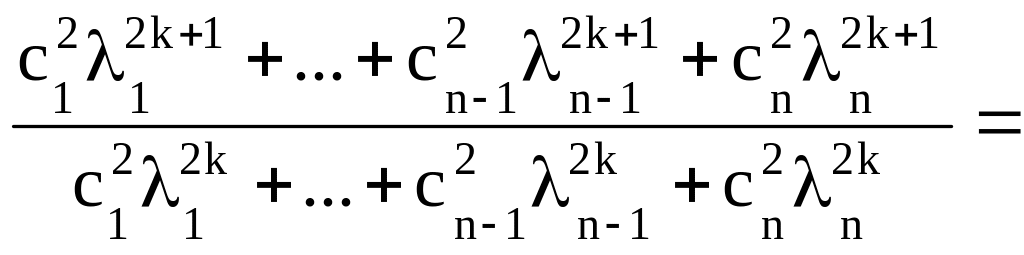
=_n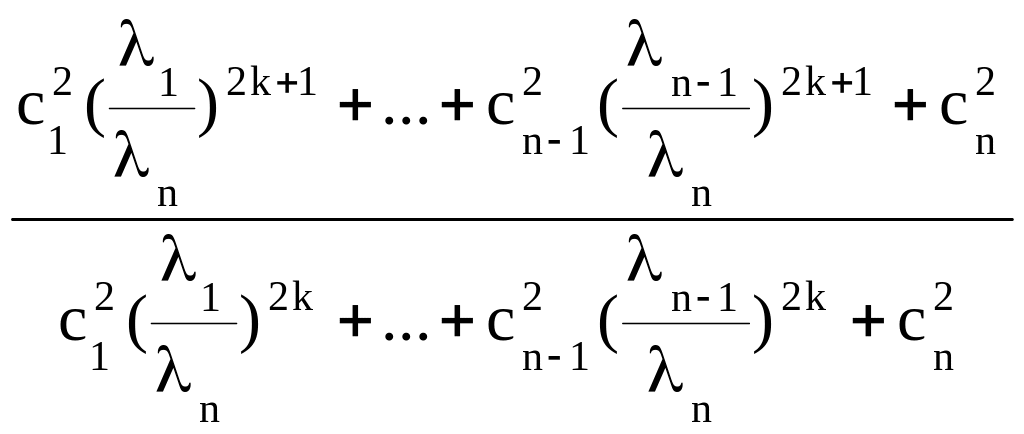 , (4.23)

что приводит к (4.21) и (4.22) при k.

Таким образом, наибольшее по модулю собственное значение находится итерационно по формуле

(k=0, 1, 2,…),

что подтверждает (4.22). Из формулы (4.23) видно, что степенной метод нахождения наибольшего по модулю собственного значения сходится при выполнении условия (4.19). Процесс итерации заканчивается при выполнении условия

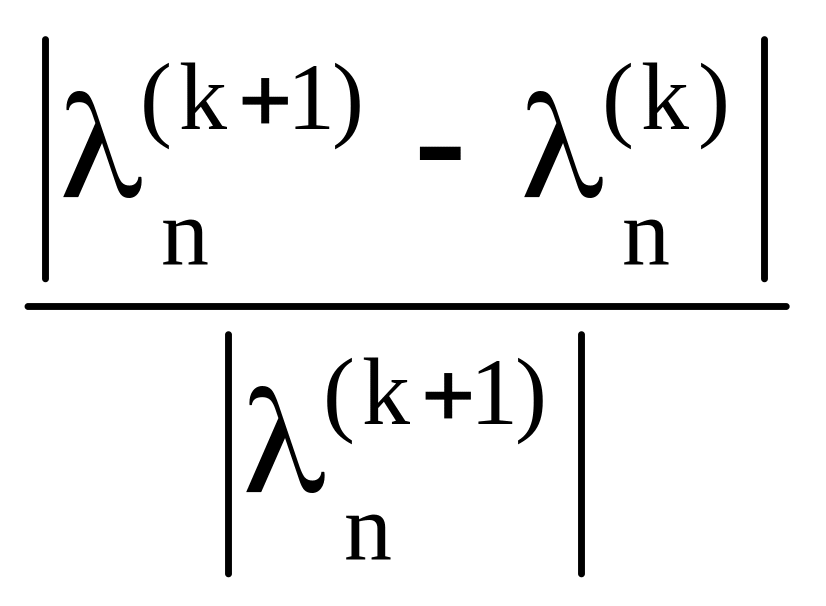<, 0<<1.

Для вычисления собственного вектора x_n воспользуемся формулой (4.20). Действительно,

y_k+1= =c_n ,

при k y_k+1 c_n x_n .

Таким образом, вектор y_k+1 отличается от собственного вектора x_n лишь множителем c_n . Так как величина может быть достаточно большой, то при вычислении x_n формулой (4.20) необходима нормировка вычисляемого вектора y_k+1 через какое-то число итерации. Нормированный собственный вектор x_n будет таким

x_n= или x_ni= .