Составители: к.т.н., доцент Данович Л.М.

ст. преп. Коренева О.В.

ст. преп. Хромых А.А.

ст. преп. Пергун О.В.

УДК 512.642+514.12(07)

МАТЕМАТИКА:

Элементы теории вероятностей, математической статистики и

линейного программирования: учебно-методическое пособие по изучению дисциплины и выполнению контрольных работ для студентов-заочников 1-го курса экономических специальностей МИППС / КубГТУ; Л.М. Данович, О.В. Коренева, А.А. Хромых, О.В. Пергун. – Краснодар 2010. – 57 с.

В учебно-методическом пособии изложены программа дисциплины, приведен краткий теоретический материал в рамках программы курса. Предложены варианты контрольных индивидуальных заданий для самостоятельного решения, а так же приведены примеры выполнения и требования к оформлению контрольных работ и рекомендуемая литература.

Печатается по решению методического совета Кубанского государственного технологического университета.

Рецензенты: к.т.н., доц. кафедры прикладной математики

КубГТУ Наумова Н.А.;

к.ф.-м.н., доц., зав. кафедрой математики и информатики

КВВУЛ Жучкова В.В.

Содержание

Введение …………………………………………………………………	4
Программа дисциплины ………………………………………………..	4
Тема 1. Теория вероятностей …………………………………………..	5
Тема 2. Элементы математической статистики ………………………	11
Тема 3. Линейное программирование ………………………………...	13
Задания к контрольной работе ……………………………………..….	32
Содержание и оформление контрольной работы …………………….	52
Вопросы для подготовки к экзамену (зачету) ………………………...	53
Список рекомендуемой литературы …………………………………...	55

Введение

В процессе изучения курса «Математика: Элементы теории вероятностей, математической статистики и линейного программирования» студент должен знать математические методы и их применение:

• в теории вероятностей и математической статистике;

• в линейном программировании.

Приобрести знания, умения и выработать навыки в соответствии со следующими требованиями:

• знать основные элементы теории вероятностей – случайные события и величины, операции над ними;

• знать основные понятия и формулы математической статистики;

• знать алгоритмы решения задач линейного программирования.

Программа дисциплины

Тема 1. Теория вероятностей.

Основные понятия теории вероятностей. Случайные события и операции над ними. Полная группа случайных событий. Определение вероятности. Комбинаторика.

Свойства вероятностей. Теорема сложения. Статистическое определение вероятности. Условная вероятность. Теорема умножения. Формула полной вероятности. Формула Байеса.

Схема Бернулли повторных испытаний, наивероятнейшее число появлений событий. Локальная и интегральная предельные теоремы и их применение.

Тема 2. Элементы математической статистики.

Основные понятия. Генеральная и выборочная совокупности. Оценки параметров распределения выборки, методы их получения.

Тема 3. Линейное программирование.

Решение систем линейных уравнений методом Жордана – Гаусса. Постановка задачи линейного программирования. Графический способ решения ЗЛП. Алгоритм решения ЗЛП симплекс – методом. Транспортная задача.

Теория верятностей

ЭЛЕМЕНТЫ КОМБИНАТОРИКИ

Комбинаторика – наука, изучающая количества комбинаций, подчиненных определенным условиям.

Перестановками называются комбинации, состоящие из одних и тех же различных элементов и отличающихся только порядком их следования.

Число всех перестановок без повторений равно

Пример 1. Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в число один раз?

Решение: .

Ответ: 6 чисел (123, 213, 231, 132, 312, 321).

Размещениями называются комбинации, составленные из элементов по элементов в каждой, которые отличаются либо составом, либо их порядком.

Число всех размещений без повторений равно

.

Пример 2. Сколько различных двузначных чисел можно составить из цифр 1, 2, 3, 4, если каждая цифра входит в изображение числа один раз?

Решение: .

Ответ: 12 чисел (12, 13,14, 21, 23, 24, 31, 32, 34, 41, 42, 43).

Сочетаниями называются комбинации, составленные из элементов по элементов в каждой, которые отличаются только составом.

Число всех сочетаний без повторений равно

.

Пример 3. Сколькими способами можно выбрать две цифры из четырех?

Решение: (первая и вторая, первая и третья, первая и четвертая, вторая и третья, вторая и четвертая, третья и четвертая).

Ответ: 6 способов.

Правило суммы. Если множество можно выбрать n способами, а множество – способами, то множество «либо , либо » можно выбрать способами.

Пример 4. Если в комнате находятся два кресла и три стула, то вошедший может присесть 2+3=5 способами: либо на первое кресло, либо на второе, либо на первый стул, либо на второй, либо на третий.

Правило произведения. Если множество можно выбрать n способами, а множество – способами, то пара может быть выбрана (nm) способами (одновременное выполнение).

Пример 5. Из Киева до Чернигова можно добраться пароходом, поездом, автобусом или самолетом. Из Чернигова до Ново-Северского пароходом или автобусом. Таким образом, путешествие из Киева до Ново-Северского можно осуществить 42 = 8 способами:

пароход

Киев поезд Чернигов пароход Ново-Северский

автобус автобус

самолет

СЛУЧАЙНЫЕ СОБЫТИЯ.

КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ

Основными понятиями в теории вероятностей являются понятия события и вероятности события.

Событие – это такой результат эксперимента или наблюдения, который при реализации данного комплекса условий может произойти или не произойти.

События будем обозначать буквами , , …

Пример 6. Стрелок стреляет по мишени.

Тогда – «выстрел» - это испытание, а ={попадание} – это событие.

Если событие неизбежно произойдет при любых условиях, то оно называется достоверным. Если событие не может произойти при любых условиях, то его называют невозможным.

Если событие при реализации некоторых условиях может произойти, а может не произойти, то оно называется случайным.

Сумма (объединение) двух событий и – это событие , состоящее в наступлении или , или , или и одновременно (хотя бы одного из них). Обозначается .

Произведение (совмещение) двух событий и – это событие , состоящее в наступлении и , и (оба наступают). Обозначается .

События называются несовместными, если появление одного из них исключает появление других событий в одном и том же испытании.

Полной группой событий называется несколько попарно несовместных событий таких, что в результате испытания появится одно и только одно из этих событий (как правило, это всевозможные исходы испытания). Обозначается .

Пример 7. Бросают две монеты.

Тогда множество  состоит из трех событий , , :

= {обе выпали орлом},

= {обе выпали решкой},

= {одна выпала орлом, а другая – решкой}.

Два несовместных события, образующих полную группу, называются противоположными. Обозначают и .

Пример 8. Подбрасывают одну монету. Тогда = {выпал орел}, а

= {выпала решка}.

Замечание: Событие – достоверное событие, а событие

– невозможное.

Для количественной оценки появления случайного события А вводится понятие вероятности.

Вероятностью события называют отношение числа благоприятных для исходов испытания к общему числу исходов. Если обозначить – число благоприятных для исходов, а – число всевозможных, то

.

(классическое определение вероятности)

Пример 9. Найти вероятность выпадения «герба» при одном бросании монеты.

Решение: (т.к. при одном бросании «герб» может выпасть только один раз), а (общее количество исходов испытания).

Значит, .

Ответ: 0,5.

Свойства вероятности:

1) Пусть – достоверное событие, тогда любой исход испытания благоприятен наступлению ,

т. е. , тогда .

2) – невозможное событие, тогда ни один исход испытания не будет благоприятствующим,

т. е. , тогда .

3) – случайное событие, , тогда , т. е. .

4) .

Замечание. Вероятности противоположных событий удобнее обозначать буквами и : ,

Пример 10. В урне 12 шаров: 3 белых, 4 черных и 5 красных. Какова вероятность вынуть один черный шар?

Решение: Вообще один шар можно достать 12 способами  , а черный шар можно достать 4 способами . Тогда , где ={достали черный шар}.

Ответ: .

Пример 11. В урне 5 белых и 8 черных шаров. Вынули сразу два шара. Какова вероятность того, что оба они белые.

Решение: Число всевозможных исходов испытания равно

(взять 2 из 13);

а число благоприятных для события = {оба шара белые} равно

(взять 2 белых из 5 белых).

Тогда .

Ответ: .

Пример 12. В цехе работают 6 мужчин и 4 женщины. По табельным номерам отобраны 7 человек. Какова вероятность того, что среди отобранных лиц будут три женщины.

Решение: Число всевозможных исходов испытания равно:

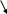10 (выбрать 7 человек из 10); а число

6_м 4_ж благоприятных для А={из 7 отобранных 3 женщины} равно:

7 (выбрать 3 женщин из 4 и

4_м 3_ж четырех мужчин из 6).

Тогда .

Ответ: 0,5.

ТЕОРЕМЫ СЛОЖЕНИЯ И УМНОЖЕНИЯ.

УСЛОВНАЯ ВЕРОЯТНОСТЬ

Теорема 1 (сложения):

Если события и несовместны, то вероятность наступления хотя бы одного из событий равна сумме вероятностей этих событий, т.е.

.

Эта теорема обобщается на случай произвольного числа попарно несовместных событий:

.

Теорема 2 (сложения):

Вероятность наступления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного наступления:

.

Событие называется независимым от события , если появление события не зависит от появления события . В противном случае события называются зависимыми.

Условной вероятностью называется вероятность события , вычисленная в предположении, что событие уже произошло.

Теорема 3 (умножения):

Вероятность совместного появления двух событий и равна

.

(причем неважно, которое из событий считать первым, а которое – вторым).

Если события и независимы, то теорема умножения примет вид:

.

Аналогично теорема умножения распространяется на случай нескольких событий:

для зависимых: ,

для независимых: .

Пример 13. Найти вероятность совместного поражения цели двумя орудиями, если вероятность поражения первым равна 0,8, а вторым – 0,7.

Решение: Обозначим: А={поражение первым орудием}, В={поражение вторым орудием}. Тогда =0,80,7=0,56 по теореме умножения для независимых событий.

Ответ: 0,56.

Пример 14. Два орудия произвели залп по цели. Вероятность поражения цели одним из них равна 0,8, а вторым – 0,7. Найти вероятность того, что цель была поражена только одним орудием.

Решение: По условию =0,8 =0,2; =0,7 =0,3.

Очевидно, что , где ={цель поражена только одним орудием}, ={цель поражена только первым}, ={цель поражена только вторым}. По теореме сложения для несовместных событий . Причем , a – по теореме умножения для независимых событий.

Тогда = 0,80,3 + 0,20,7 = 0,38.

Ответ: 0,38.

Пример 15. Студент разыскивает формулу в трех справочниках. Вероятности того, что формула окажется в первом, втором, третьем справочниках соответственно равны 0,6, 0,7 и 0,8. Найти вероятности того, что формула окажется:

1) только в одном справочнике;

2) только в двух справочниках;

3) во всех трех справочниках.

Решение: По условию ;

;

.

1) Пусть ={формула только в одном справочнике}, тогда

=0,60,30,2 + 0,40,70,2 + 0,40,30,8 = 0,188.

2) Пусть ={формула только в двух справочниках}, тогда

=0,60,70,2+0,40,70,8 + 0,60,30,8 = 0,452.

3) Пусть ={формула во всех трех справочниках}, тогда

= 0,60,70,8 = 0,336.

Ответ: 1) 0,188; 2) 0,452; 3) 0,336.

Теорема 4 (вероятность появления хотя бы одного события).

Пусть известны вероятности появления каждого из независимых событий: , , …, , тогда вероятность появления хотя бы одного из них равна , где .

Пример 16. Студент разыскивает формулу в трех справочниках. Вероятности того, что формула окажется в первом, втором, третьем справочниках соответственно равны 0,6, 0,7 и 0,8. Найти вероятность того, что формула окажется хотя бы в одном справочнике.

Решение: По условию ;

;

.

Пусть ={формула хотя бы в одном справочнике}, тогда

=1 – 0,40,30,2 = 0,976.

Ответ: 0,976.

ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ. ФОРМУЛА БАЙЕСА

Если известно, что событие может произойти вместе с одним из событий (гипотез), образующими полную группу событий, то вероятность события равна

.

Эта формула называется формулой полной вероятности.

Пример 17. Литье в болванках для дальнейшей обработки поступает из двух цехов: 70% из первого и 30% из второго. При этом материал первого цеха имеет 10% брака, а второго – 20%. Найти вероятность того, что одна наудачу взятая болванка не имеет дефектов.

Решение: Введем обозначения: ={болванка без дефектов},

={материал из 1^го цеха},

={материал из 2^го цеха}.

Тогда по условию =0,7, =0,3;

=1-0,1=0,9, =1-0,2=0,8.

Значит, по формуле полной вероятности получаем:

= 0,70,9 + 0,30,8 = 0,87.

Ответ: 0,87.

Условная вероятность события в предположении, что событие уже произошло, определяется по формуле Байеса:

,

где вычисляют по формуле полной вероятности.

Пример 18. Литье в болванках для дальнейшей обработки поступает из двух цехов: 70% из первого и 30% из второго. При этом материал первого цеха имеет 10% брака, а второго – 20%. Найти вероятность того, что наудачу взятая не имеющая дефектов болванка из первого цеха.

Решение: Введем обозначения: ={болванка без дефектов},

={материал из 1^го цеха},

={материал из 2^го цеха}.

Тогда по условию =0,7, =0,3;

=1-0,1=0,9, =1-0,2=0,8.

И значит, по формуле Байеса проверим первую гипотезу: , где вычислили в примере17.

Ответ: 0,724.

ПОВТОРНЫЕ ИСПЫТАНИЯ. ФОРМУЛА БЕРНУЛЛИ

Если производится независимых испытаний, в каждом из которых вероятность появления события одна и та же и равна ( ), то вероятность того, что событие появится в этих испытаниях ровно раз можно вычислить по формуле Бернулли:

, где .

Пример 19. Вероятность выиграть по лотерейному билету равна . Найти вероятность выиграть по двум билетам из пяти.

Решение: По условию = , значит = ; = 5, = 2. Тогда по формуле Бернулли получаем

P₅(2)= = =0,1285.

Ответ: 0,1285.

Замечание: если число испытаний n велико, то применение формулы Бернулли приводит к громоздким вычислениям. В таких случаях пользуются предельными теоремами Лапласа.