Кінцево-різницевий метод

Розглянемо двоточкову крайову задачу для лінійного диференційного рівняння другого порядку на відрізку :

, (8.8)

. (8.9)

Введемо різницеву сітку на відрізку :

.

Рішення задачі (8.8), (8.9) шукається у вигляді сіткової функції , припускаючи, що рішення існує і воно є єдиним. Введемо різницеву апроксимацію похідних наступним чином:

,

. (8.10)

Підставляючи апроксимації похідних з (8.10) у (8.8) і (8.9), одержимо систему рівнянь для знаходження :

Звідси одержимо систему лінійних алгебраїчних рівнянь з тридіагональною матрицею коефіцієнтів:

(8.11)

Для системи (8.11) при достатньо малих кроках сітки і виконані умови переваги діагональних елементів:

, (8.12)

що гарантує стійкість обчислень та коректність застосування методу прогонки для вирішення цієї системи.

У випадку використання граничних умов другого та третього роду апроксимація похідних здійснюється за допомогою односторонніх різниць першого та другого порядку:

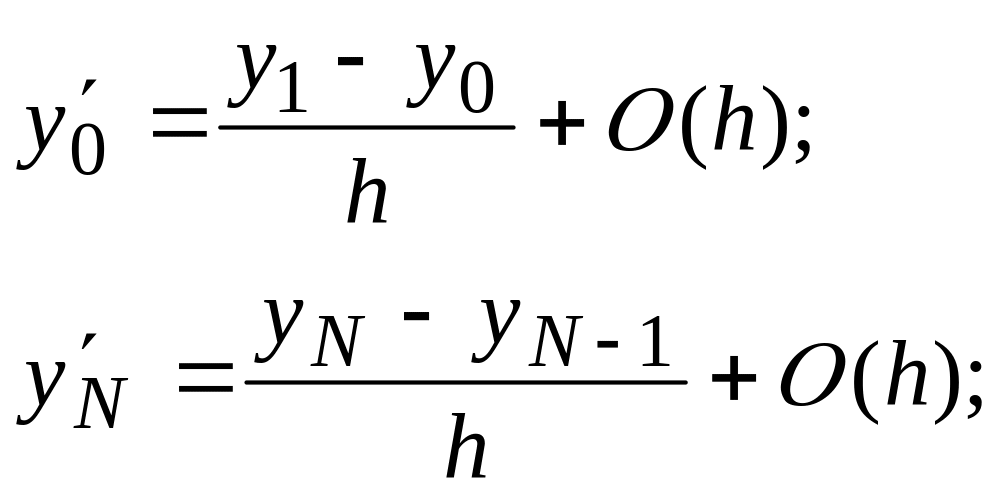(8.13)

(8.14)

У випадку використання формул (8.13) лінійна алгебраїчна система апроксимує диференційну задачу в цілому тільки з першим порядком (через апроксимацію в граничних точках), однак зберігається тридіагнональна структура матриці коефіцієнтів. У випадку використання формул (8.14) другий порядок апроксимації зберігається всюди, але матриця лінійної системи не тридіагнональна.

Перевагою кінцево-різницевого методу є те, що він дозволяє звести ров’язок крайової задачі до ров’язку системи алгебраїчних рівнянь.

Приклад 8.2

Розв’язати крайову задачу із заданими крайовими умовами з кроком

Виконаємо заміну: , , , , оскільки на інтервалі з кроком буде 5 підінтервалів, то , , , , , .

В усіх внутрішніх вузлах відрізка після заміни їх похідних різницевими аналогами одержуємо:

.

На лівій границі , на правій границі апроксимуємо похідну односторонньою різницею 1-го порядку: . За допомогою групування доданків, приведення подібних членів, підстановки значень , та з врахуванням , одержуємо систему лінійних алгебраїчних рівнянь:

В даній тридіагональній системі виконана умова , тобто діагональні елементи за модулем більші, ніж сума інших елементів системи за модулем. Отже, для розв’язання цієї системи можна використати метод прогонки.

В результаті розв’язання системи методом прогонки отримані наступні значення: , , , , .

Розв’язком крайової задачі є таблична функція (табл. 8.3).

Таблиця 8.3

	0	1	2	3	4	5
	0	0,2	0,4	0,6	0,8	1,0
	1,0	0,77191	0,58303	0,43111	0,31265	0,22332