Основные законы распределения целочисленных случайных величин

Определение целочисленной случайной величины. Производящая функции и её свойства. Биномиальный, пуассоновский, геометрический и равномерный законы распределения, производящие функции для этих законов распределения и их числовые характеристики. Гипергеометрический закон распределения.

Производящие функции

Среди дискретных случайных величин особенно важны величины, принимающие только целые значения 0, 1, 2, … Такие случайные величины называются целочисленными. Для изучения таких величин вводится понятие производящей функции. Пусть  – целочисленная случайная величина с распределением вероятности 

Функция комплексного аргумента 

называется производящей функцией данного распределения. Ряд (7.1) сходится по крайней мере в единичном круге  . Укажем основныесвойства производящей функции.

Свойство 1.  .

Свойство 2. Математическое ожидание случайной величины выражается формулой

Свойство 3. Дисперсия случайной величины выражается формулой

Таким образом, производящую функцию можно использовать для нахождения числовых характеристик целочисленных случайных величин. Более того, она полностью задаёт закон распределения этих величин.

Рассмотрим наиболее часто встречающиеся законы распределения целочисленных случайных величин.

Биномиальный закон (распределение Бернулли)

В общей форме биномиальный закон описывает осуществление признака в   испытаниях с возвратом. Наглядной схемой таких испытаний является последовательный выбор с возвращением шаров из урны, содержащей   белых и   чёрных шаров. Если   — число появления белых шаров в выборке из   шаров, то

где   — вероятность появления при одном извлечении соответственно белого и чёрного,

Производящая функция биномиального распределения задаётся формулой

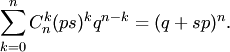
Основные характеристики биномиального распределения (математическое ожидание и дисперсия):

Пример 1. Вероятность получения бракованного изделия равна 0,01. Какова вероятность того, что среди 100 изделий окажется не более 3 бракованных?

Решение. Пусть  . Согласно биномиальному закону и закону сложения имеем

Подробнее о распределении Бернулли см. часть 3.

Закон распределения Пуассона (закон редких событий)

Случайная величина   называется распределённой по закону Пуассона с параметром  , если

Производящая функции распределения Пуассона задаётся формулой

Характерной особенностью распределения Пуассона являются совпадения математического ожидания и дисперсии, причём

Распределение Пуассона можно получить из биномиального распределения путёмпредельного перехода при   при условии   и в этом случае интерпретируется как закон “редких” явлений. Если   достаточно велико, a   мало, то формулу Пуассона (7.3) часто используют в качестве приближения вместо точных биномиальных формул для вероятностей   успехов в   испытаниях (подробнеесм. часть 3).

Пример 2. На факультете насчитывается 500 студентов. Какова вероятность того, что первое сентября является днём рождения одновременно для   студентов данного факультета? Вычислить указанную вероятность для значений  .

Решение. Так как   и вероятность родиться первого сентября любому из студентов факультета   то можно считать, что случайное число студентов   родившихся первого сентября, подчиняется закону распределения Пуассона с параметром   Поэтому, по формуле (7.3), имеем

Далее рекуррентно находим

К случайным величинам, подчинённым закону Пуассона, приводит большое количество задач, относящих к вопросам массового обслуживания. В качестве примера рассмотрим работу телефонной станции. Можно доказать, что при выполнении некоторых условий вероятность   вызовов за промежуток времени   определяется формулой

 где   — количество вызовов.

Если положить   то последняя формула означает, что случайная величина распределена по закону Пуассона.